Chapter 5 Un proof-checker per i file CIC della libreria

In questo capitolo descriveremo brevemente la progettazione e l'implementazione di un proof-checker per i file CIC della libreria di HELM. Entrambe non sono ancora state completate, in quanto non è stata ancora considerata la stratificazione degli universi, ovvero tutti i Type(i) sono rappresentati da Type¹. Il proof-checker verrà completato quanto prima, probabilmente entro la fine del 2000.

Le motivazioni dello sviluppo del proof-checker sono molteplici:

La scrittura del proof-checker ha permesso di determinare se tutta l'informazione degli oggetti CIC è stata esportata.
Il proof-checker rappresenta la dimostrazione concreta della possibilità di reimplementare tutte le funzionalità dei moderni proof-assistant monolitici in maniera modulare, basandosi sul formato XML. In particolare, l'architettura e l'implementazione risultanti sono estremamente più semplici ed eleganti di quelle del proof-checker integrato in Coq. Inoltre, nonostante il codice non sia stato particolarmente ottimizzato e gli algoritmi adottati siano fra i più semplici noti, le prestazioni del proof-checker sono comparabili a quelle di Coq, se si escludono le rispettive fasi di parsing.
A partire da una implementazione completa e funzionante del proof-checker, diventa possibile sperimentare modifiche al sistema logico, per esempio per affrontare il problema delle dimensioni delle prove.
Alcune sottigliezze del sistema logico possono essere comprese solamente durante la progettazione e l'implementazione di un proof-checker, che assumono, quindi, importanti valenze didattiche.

Inoltre, il nostro proof-checker è il primo, a conoscenza degli autori, a gestire dinamicamente gli ambienti, utilizzando esclusivamente l'ordinamento parziale generato dalle dipendenze fra gli oggetti (vedi pagina 59).

Sono state prese due importanti decisioni preliminari alla progettazione. La prima è sull'obiettivo dello sviluppo, che è mirato all'ottenimento di un prototipo. Pertanto, la performance viene tenuta in secondo piano rispetto alla pulizia dell'architettura e alla semplicità dell'implementazione. Ciò nonostante, i risultati ottenuti sono stati decisamente buoni, anche sul piano delle prestazioni.

La seconda decisione riguarda la scelta del linguaggio di programmazione: l'intero proof-checker è sviluppato in OCaml. Il linguaggio si è già dimostrato ottimale nell'ambito dello sviluppo di type-checker. Infatti, i tipi di dati concreti di OCaml permettono una definizione compatta ed elegante della sintassi di CIC, mentre il paradigma funzionale e il garbage collector rendono concisa l'implementazione e permettono di definire funzioni aderendo strettamente alle regole di tipaggio date nel capitolo 2.1. Il fatto che anche Coq sia implementato in OCaml semplifica il riutilizzo del codice². Inoltre, l'estrema concisione della sintassi di OCaml, dovuta principalmente alla type-inference, e la caratteristica del linguaggio di essere fortemente tipato rendono la produttività in fase di implementazione mediamente molto alta, con un numero quasi nullo di errori di tipo non logico. Il complesso sistema di moduli del linguaggio permette di sfruttare moderne tecniche di ingegneria del software usualmente applicabili quasi esclusivamente nell'ambito dei linguaggi ad oggetti. Infine, per quei compiti per i quali il paradigma funzionale non è maggiormente adatto o è poco conciso, è possibile utilizzare feature imperative e, quando il sistema dei moduli si rivela insufficiente, ricorrere agli oggetti, che possono essere utilizzati sia in maniera funzionale che imperativa.

Nelle successive due sezioni descriveremo brevemente rispettivamente la progettazione e l'implementazione del prototipo. Si assume non solo un'ottima comprensione dell'intera sezione 2.1 che descrive CIC e dei paragrafi 2.2.1, 2.2.2 e 2.2.4 che descrivono le estensioni di Coq, ma anche una buona conoscenza sull'implementazione di type-checker per l-calcoli basati sulla rappresentazione delle variabili con indici di DeBrujin.

5.1 Progettazione

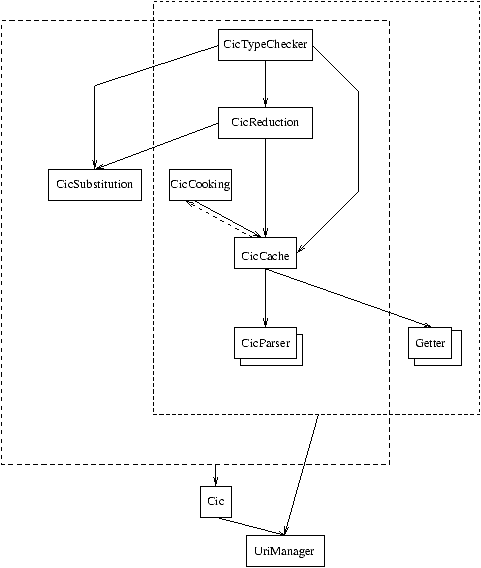
Figura 5.1: Grafo delle dipendenze per i moduli dell'implementazione del typechecker

In figura 5.1 viene mostrato il grafo delle dipendenze dei moduli del typechecker, cosí come deciso in fase di progettazione. La buona norma di evitare dipendenze cicliche fra moduli non può essere violata in OCaml. Pertanto, già in fase di progettazione, è bene discriminare le dipendenze in statiche e dinamiche per eliminare i cicli. Una freccia solida da un modulo A verso un modulo B significa che A dipende staticamente, ovvero in fase di compilazione, da B. Una freccia tratteggiata da A verso B, invece, indica una dipendenza dinamica: a run-time il modulo B registrerà una o più sue funzioni presso il modulo A affinché questo le richiami³. Tutti i moduli racchiusi in un rettangolo tratteggiato dipendono direttamente da tutti i moduli che sono bersaglio di una freccia con sorgente il riquadro. Il simbolo formato con rettangoli sovrapposti indica un metamodulo, ovvero un modulo logico che è a sua volta decomposto in altri moduli logici. In particolare, il metamodulo getter è già stato descritto nel capitolo 4.1.1, dove in figura 4.1 sono state indicate le dipendenze fra i moduli logici che lo compongono.

Passiamo ora a descrivere individualmente i singoli (meta)moduli.

5.1.1 UriManager

È un sotto-modulo, nel senso dell'ereditarietà nei linguaggi ad oggetti, di quello descritto nel paragrafo 4.1.1; pertanto, una sua implementazione può sostituire quella dell'omonimo modulo nel metamodulo Getter. Lo scopo del modulo è fornire un tipo di dato astratto uri con le relative operazioni richieste durante l'implementazione del type-checker. La sua interfaccia, o signature, è:

type uri
val eq : uri -> uri -> bool
val uri_of_string : string -> uri
val string_of_uri : uri -> string  (* complete uri *)
val name_of_uri   : uri -> string  (* name only (without extension)*)
val buri_of_uri   : uri -> string  (* base uri only *)
val depth_of_uri  : uri -> int     (* length of the path *)

(* relative_depth curi uri cookingsno                            *)
(* is the number of times to cook uri to use it when the current *)
(* uri is curi cooked cookingsno times                           *)
val relative_depth : uri -> uri -> int -> int

I primi quattro elementi sono gli stessi già descritti nel paragrafo 4.1.1. Le successive tre funzioni sono di uso frequente. L'ultima è tecnica e verrà richiamata dal meccanismo di cottura: restituisce il numero di volte che un oggetto di cui viene specificato l'URI deve essere cucinato per essere utilizzato durante il type-checking di un altro oggetto di cui viene indicato l'URI e il numero di cotture subite. Con ``numero di cotture'', a differenza di quanto accade in Coq, non indichiamo il numero di ingredienti astratti, bensí la differenza fra la lunghezza dell'URI dell'oggetto prima e dopo la cottura. Quest'uso è coerente con l'osservazione che un oggetto viene sempre cucinato rispetto a tutti o nessuno degli ingredienti definiti in una stessa sezione.

Raffinamento della specifica

Poiché gli URI vengono utilizzati pesantemente sia nella rappresentazione interna dei l-termini, sia durante il type-checking, si impongono, per motivi prestazionali, dei vincoli sia sulla complessità computazione delle funzioni, sia sull'occupazione in spazio della rappresentazione degli URI:

Due URI identici devono condividere la stessa rappresentazione. In altre parole, la uri_of_string, se richiamata due volte su stringhe uguali, deve restituire in entrambi i casi la stessa (in senso fisico) struttura dati.
Le funzioni eq, string_of_uri, name_of_uri, buri_of_uri e depth_of_uri devono appartenere a O(1).
La funzione relative_depth deve appartenere a O(depth_of_uri(u)) dove u è l'URI dato in input.

Per ottenere complessità computazionali cosí basse diventa necessario ricorrere a una rappresentazione degli URI decisamente elaborata. Come conseguenza, è lecito aspettarsi un'alta complessità computazionale per la uri_of_string. Ciò nonostante, poiché capita frequentemente che, durante il proof-checking di un oggetto, si incontri lo stesso URI più volte, viene richiesto un ulteriore vincolo sulla complessità di tale funzione:

La complessità computazionale media della depth_of_uri su un URI già incontrato deve essere al più O(log(n)) dove n è il numero di URI già incontrati.

5.1.2 Cic

Questo modulo, privo di funzioni, fornisce esclusivamente la rappresentazione concreta dei termini e degli oggetti di CIC. La sua signature viene interamente riportata, per comodità di consultazione, in appendice B.

Confrontando attentamente la rappresentazione XML in appendice A con quella OCaml e con la sintassi di CIC descritta nel paragrafo 2.1.1, si individuano facilmente le seguenti discrepanze⁴:

Lo zucchero sintattico è scomparso, riavvicinandosi alla rappresentazione data nella descrizione della teoria. In particolare, i binder, che nella rappresentazione XML erano stati spostati sull'elemento target, sono tornati ad essere attributi di Lambda o Prod.
Tutti gli URI, che in XML erano in parte assoluti e in parte relativi, hanno la stessa rappresentazione interna, determinata dal modulo UriManager.
Tutti gli URI che si riferiscono ad oggetti cucinabili hanno sempre associato un indice, indicato in commento con cookingsno, che indica il livello di cottura voluto per l'oggetto. Questo deve essere calcolato durante il parsing e modificato ad ogni cottura dell'oggetto. Il motivo che ci ha spinto ad esplicitare l'indice, che poteva comunque essere calcolato al volo all'occorrenza, è dovuto alla complessità computazione dell'operazione, che, pur non essendo troppo elevata (vedi paragrafo 5.1.1), diventava influente per l'alto numero di applicazioni della funzione relative_depth che sarebbero state richieste.
La rappresentazione interna degli ingredienti di un oggetto è una buona sintesi, in termini di efficienza, fra quella dei file XML e quella come lista di coppie. In pratica, è una lista di liste di URI avente un elemento per ogni token numerico presente nel file XML, ovvero per ogni livello di cottura; la lista elemento contiene tutti gli URI degli ingredienti per quel livello.
La rappresentazione OCaml dei costruttori prevede un ulteriore parametro, assente sia nella teoria che nel DTD XML, che è un reference ad una lista di booleani, possibilmente non specificata: durante il parsing, la lista non viene specificata; durante il proof-checker del tipo induttivo del costruttore, vengono individuati i parametri in cui il costruttore è ricorsivo, nel senso del paragrafo 2.10, e l'informazione viene memorizzata nella lista di booleani per essere poi utilizzata più volte durante le verifiche delle condizioni GC e GD, con conseguente incremento delle prestazioni.

5.1.3 CicParser

Il compito di questo metamodulo è semplicemente quello, dato un file XML che descrive un oggetto CIC, di restituirne la rappresentazione interna. Pertanto, la sua signature è formata da una sola funzione:

val term_of_xml : string -> UriManager.uri -> Cic.obj

dove il primo parametro è il pathname del file XML e il secondo il suo URI, necessario per risolvere gli URI relativi durante il parsing.

Raffinando la progettazione, si è deciso di implementare il metamodulo utilizzando tre distinti moduli, chiamati CicParser, CicParser2, CicParser3. Il primo ha il compito di costruire l'albero di sintassi astratta associato al file XML⁵; il secondo si occupa della creazione, a partire da questo, della rappresentazione interna a livello degli oggetti; il terzo fa lo stesso, ma a livello dei termini. Nella sezione dedicata all'implementazione si mostrerà il grafo delle dipendenze fra i moduli e si accennerà brevemente alle signature degli ultimi due.

5.1.4 CicCache

Questo è sicuramente il modulo dall'interfaccia più complessa. I suoi compiti principali sono quello di fungere da cache per incrementare le prestazioni nell'accesso agli oggetti e quello di nascondere l'utilizzo del Getter e del CicParser ai moduli dei livelli soprastanti. Poiché il parsing dei file XML è un'operazione molto costosa in termini di tempo, il cache deve evitare il più possibile un cache miss, eliminando gli elementi esclusivamente quando strettamente necessario. Il parsing non è, però, la sola operazione critica compiuta sugli oggetti: la loro cottura, infatti, richiede la visita esaustiva dei loro termini e l'accesso a tutti gli oggetti in essi riferiti. Pertanto, dopo aver sviluppato un primo prototipo del proof-checker in cui la cottura veniva effettuata al volo, abbiamo deciso di mantenere in cache non solo la versione meno cucinata di un oggetto, ma anche tutte quelle parzialmente o totalmente cotte, ottenendo un sensibile incremento delle prestazioni. La decisione, però, introduce una inevitabile circolarità fra le operazioni di accesso al cache, cottura e type-checking: un oggetto può essere cucinato esclusivamente se ha già superato il proof-checking; per il suo type-checking e la cottura, però, è necessario utilizzare il cache per ottenere la definizione dell'oggetto e di quelli da questo riferiti. Il punto chiave che ha permesso di risolvere, in parte, la circolarità sono le seguenti osservazioni, derivate da una semplice analisi delle regole di tipaggio di CIC e da quelle di introduzione di oggetti nell'ambiente:

Il grafo diretto delle dipendenze fra gli oggetti di CIC è aciclico⁶.
Anche se la riduzione è definita per termini qualsiasi, ai fini del proof-checking può essere sempre richiamata esclusivamente su termini che abbiano già superato il type-checking.

Come conseguenza, è possibile definire il cache in modo che mantenga gli oggetti in una delle seguenti tre forme: non cucinata e non type-checked, congelata, cucinata a tutti i livelli possibili. Quando il termine viene richiesto per la prima volta, lo si scarica ricorrendo al getter e se ne ottiene la forma non cucinata e non type-checked utilizzando il parser. Per effettuarne il type-checking, si deve comunicarne l'intenzione al cache, che passerà l'oggetto alla forma congelata, ma, quando richiesto, continuerà a restituirlo nella forma precedente. Infine, la terminazione del type-checking deve essere comunicata al cache, che invoca il meccanismo di cottura per ottenere lo stesso oggetto cucinato ad ogni possibile livello, passandolo alla terza forma. Solo da questo momento in avanti sarà possibile accedere alle forme cucinate.

Il meccanismo appena descritto permette di risolvere elegantemente la dipendenza circolare fra il type-checker e il modulo responsabile della cottura e quella fra il type-checker e il cache, ma non elimina quello fra il modulo di cottura e il cache. Poiché il cache non dovrebbe avere, almeno intuitivamente, alcuna dipendenza dal meccanismo di cottura, che è strettamente dipendente dal sistema logico, diventa naturale mantenere la dipendenza statica fra il modulo di cottura e il cache, rendendo dinamica quella in senso opposto.

Considerate tutte le precedenti osservazioni, si è scelta la seguente signature per il modulo, dove il costruttore delle forme congelate viene tenuto nascosto grazie ai meccanismi di information hiding di OCaml:

exception CircularDependency of string;;

(* get_obj uri                                                   *)
(* returns the uncooked form of the cic object whose URI is uri. *)
(* If the term is not just in cache, then it is parsed via       *)
(* CicParser.term_of_xml from the file whose name is the result  *)
(* of Getter.get uri                                             *)
val get_obj : UriManager.uri -> Cic.obj

type type_checked_obj =
   CheckedObj of Cic.obj    (* cooked obj *)
 | UncheckedObj of Cic.obj  (* uncooked obj *)

(* is_type_checked uri cookingsno                               *)
(* returns (CheckedObj object) if the object has been           *)
(* type-checked otherwise it returns (UncheckedObj oject) and   *)
(* freeze the object for the type-checking                      *)
(* set_type_checking_info must be called to unfreeze the object *)
val is_type_checked : UriManager.uri -> int -> type_checked_obj

(* set_type_checking_info uri                                   *)
(* must be called once the type-checking of uri is finished     *)
(* The object whose URI is uri is unfreezed and cooked at every *)
(* possible level using the !cook_obj function                  *)
(* Therefore, is_type_checked will return a CheckedObj          *)
val set_type_checking_info : UriManager.uri -> unit

(* get_cooked_obj uri cookingsno *)
(* returns the object whose URI is uri cooked cookingsno levels *)
val get_cooked_obj : UriManager.uri -> int -> Cic.obj

val cook_obj :
 (Cic.obj -> UriManager.uri -> (int * Cic.obj) list) ref

Il significato di tutte le funzioni dovrebbe essere chiaro grazie ai commenti e alle spiegazioni precedenti. La cook_obj è la reference con la quale deve essere registrata la funzione di cottura che, dato un oggetto nella forma non cucinata e il suo URI, ritorna una lista di coppie livello di cottura---oggetto cucinato a quel livello.

5.1.5 CicCooking

La signature del modulo CicCooking è composta da una sola funzione che viene registrata presso il cache durante l'inizializzazione del modulo stesso:

val cook_obj : Cic.obj -> UriManager.uri -> (int * Cic.obj) list

La funzione deve semplicemente implementare fedelmente le regole di cottura date informalmente nel paragrafo 2.2.4.

5.1.6 CicSubstitution, CicReduction e CicTypeChecker

Questi moduli non hanno richiesto alcuno sforzo progettuale, in quanto sono assolutamente standard nella scrittura di type-checker per l-calcoli, a partire da quello tipato semplice. Chi conosce questi strumenti dovrebbe riconoscere immediatamente le funzioni descritte nelle signature dei tre moduli:

CicSubstitution:

val lift : int -> Cic.term -> Cic.term
(* subst t1 t2  substitutes t1 for the first free variable in t2 *)
val subst : Cic.term -> Cic.term -> Cic.term

CicReduction:

val whd : Cic.term -> Cic.term
val are_convertible : Cic.term -> Cic.term -> bool

CicTypeChecker:

exception NotWellTyped of string
val typecheck : UriManager.uri -> unit

5.2 Implementazione

In questa sezione si accennerà brevemente all'implementazione del proof-checker, descrivendo esclusivamente le scelte implementative non standard o quelle che hanno avuto grossi impatti dal punto di vista delle prestazioni. I moduli verranno descritti singolarmente, nello stesso ordine della precedente sezione. Infine, verranno riportate alcune statistiche.

5.2.1 UriManager

Sono state fornite tre differenti implementazioni, che utilizzano strutture dati di complessità crescente. All'aumento di complessità corrisponde, in teoria, un aumento del tempo richiesto per il primo accesso e una sua diminuzione per gli accessi successivi. Concretamente, però, nessuna delle tre soluzioni ha dato risultati superiori alle altre in tutti i casi: per teorie semplici, con pochi riferimenti fra oggetti, le soluzioni più semplici danno risultati lievemente migliori; per quelle complesse, si ha il fenomeno opposto. Effettuando statistiche sul proof-checking di tutta la libreria standard di Coq, che contiene due teorie complesse di notevoli dimensioni, quella dei numeri reali e quella della normalizzazione di espressioni su anelli, si è riscontrato un iniziale aumento delle prestazioni passando dall'implementazione più semplice a quella più complessa di circa il 15%, che si è poi ridotto notevolmente in seguito alle ottimizzazioni successivamente introdotte nella cicReduction. Pertanto, si è preferito mantenere esclusivamente l'implementazione più complessa, che ora descriveremo, che è anche l'unica che rispetta pienamente i vincoli sulla complessità computazionale introdotti in fase di progettazione nel paragrafo 5.1.1.

Ogni URI viene rappresentato internamente come un vettore contenente, in ordine lessicografico, tutti i suoi URI prefisso, seguiti dal nome dell'oggetto. Per esempio, l'URI ``cic:/a/b/c.con'' viene codificato con il vettore [| "cic:/a" ; "cic:/a/b" ; "cic:/a/b/c.con" ; "c" |]. Questa rappresentazione permette di ottenere sia la lunghezza di un URI che il nome dell'oggetto da esso riferito in O(1). Per implementare la uri_of_string, viene utilizzato un albero bilanciato di ricerca che implementa una funzione che mappa ogni URI in formato stringa nella rappresentazione interna: ad ogni invocazione della funzione, l'URI viene cercato nell'albero e restituito; solo se non presente, viene creata la sua rappresentazione interna, memorizzata nell'albero e restituita come valore di ritorno. In questo modo, come funzione eq per l'uguaglianza fra URI può essere utilizzata direttamente l'uguaglianza fisica di OCaml, che appartiene a O(1) in quanto si limita a confrontare l'indirizzo in memoria dei due valori. Lo stesso stratagemma viene utilizzato per normalizzare i prefissi utilizzati nella rappresentazione interna, ricorrendo ad un secondo albero bilanciato di ricerca. A parte l'ovvio risparmio in spazio, è in questo modo possibile implementare la relative_depth iterando in parallelo sulle rappresentazioni interne dei due URI e utilizzando l'uguaglianza fisica per confrontare fra loro i prefissi, riducendo la complessità computazionale di tutta l'operazione, che diventa lineare nella profondità dell'URI più breve. Come conseguenza negativa, il caso pessimo della creazione di un nuovo URI diventa O(n² + log m), dove n è la lunghezza in caratteri dell'URI e m il numero di URI già incontrati. Un'analisi più approfondita basata su un modello plausibile per la località dei riferimenti nella libreria, però, rivela che è possibile stimare il costo ammortizzato in solo O(k/k - 1 + log m) dove k è il numero medio di oggetti contenuti non ricorsivamente in ogni sezione.

5.2.2 CicParser

Il metamodulo, come preannunciato, è stato implementato ricorrendo a tre moduli il grafo delle cui mutue dipendenze è riportato in figura 5.2.

Figura 5.2: Grafo delle dipendenze per i moduli dell'implementazione del CicParser

Il primo modulo contiene il codice necessario per interfacciarsi con Markup, un parser XML scritto in OCaml; una volta ottenuto l'albero di sintassi astratta da Markup, vengono richiamate le funzioni del secondo modulo. Il terzo modulo prende in input un albero di sintassi astratta di Markup relativo ad un termine e ne ritorna la rappresentazione interna, di tipo Cic.term. Il secondo, che richiama il terzo, fa lo stesso per gli oggetti. La dipendenza statica e quella dinamica fra il primo modulo e il terzo sono dovute a dettagli implementativi sull'utilizzo di Markup, che espone due interfacce, una ad oggetti e una funzionale pura; il secondo modulo ricorre a quella funzionale pura, il terzo a quella ad oggetti. I motivi della scelta dell'utilizzo di entrambi i tipi di interfacce sono dovuti al trade-off fra complessità computazionale e spaziale: l'interfaccia ad oggetti diminuisce la prima grazie all'uso del late binding, ma richiede la creazione di un nuovo oggetto per ogni nodo dell'albero di sintassi astratta; quella funzionale non deve istanziare oggetti, ma è costretta ad effettuare ripetuti e costosi confronti fra stringhe per discriminare i tag dei nodi dell'albero. L'alto numero di elementi XML per il markup a livello dei termini suggerisce l'adozione dell'interfaccia ad oggetti per minimizzare il tempo di parsing. Il basso numero di elementi per il livello degli oggetti determina un basso costo computazionale anche per l'interfaccia funzionale, che non è, però, soggetta ad ulteriore costo spaziale, rendendola preferibile.

5.2.3 CicCache

L'unica osservazione di rilievo è il fatto che, almeno in questa prima implementazione, si è deciso di non eliminare mai un oggetto dal cache. Infatti, l'occupazione complessiva di memoria del proof-checker dopo la verifica di tutti gli oggetti della libreria standard di Coq è ancora sufficientemente bassa da non giustificare lo sforzo implementativo.

5.2.4 CicCooking

Sull'implementazione del meccanismo di cottura, sono necessarie due osservazioni. La prima è legata alla differente rappresentazione interna dei tipi mutuamente (co)induttivi rispetto alla descrizione teorica. Come descritto nel paragrafo 2.2.2, le occorrenze dei tipi (co)induttivi all'interno dei tipi dei loro costruttori vengono rappresentate da indici di de Brujin. Tali indici, quindi, si riferiscono ad oggetti cucinabili presenti nell'ambiente, che possono avere ingredienti. Conseguentemente, l'implementazione naïf della cottura diventa complessa, con la necessità di mantenere un contesto di cottura in cui agli indici di de Brujin vengono associati gli ingredienti richiesti dalle ``entità'' a cui essi puntano. Per ovviare al problema, è possibile utilizzare un diverso formato interno in cui anche le occorrenze dei tipi (co)induttivi all'interno dei tipi dei rispettivi costruttori sono codificate come MutInd. Come conseguenza, però, si avrebbe un aumento della complessità del type-checking. La soluzione che abbiamo adottato consiste nell'utilizzare quest'ultima forma esclusivamente per i termini cotti.

La prima operazione compiuta dalla funzione di cottura, quindi, diventa il cambio di rappresentazione per il termine ancora non cucinato. Il fatto che sia possibile far coesistere due diverse rappresentazioni senza modificare le regole di tipaggio può, a prima vista, sembrare sorprendente. Valutando attentamente la forma della regola Ind data a pagina 35 nella codifica con indici di de Brujin, però, si nota che quello che viene fatto è semplicemente anticipare la sostituzione che andrebbe effettuata ogni volta che la regola viene applicata.

La seconda osservazione sul meccanismo di cottura è legata alla scelta, nella nostra rappresentazione interna, di associare ad ogni URI il numero di volte che l'oggetto puntato deve essere cucinato. Cosí facendo, un oggetto A che non dipenda da nessun ingrediente e l'oggetto A', ottenuto cucinando A di un livello, differiscono nella rappresentazione interna esclusivamente per tali indici. La conseguenza è la necessità di mantenere in cache copie praticamente identiche degli oggetti, con enorme spreco di memoria dovuto al fatto che, normalmente, un oggetto ha ingredienti solamente ad una piccola percentuale dei livelli possibili. Riguardando attentamente la definizione di cottura data nel paragrafo 2.2.4, è facile convincersi del seguente fatto: gli ingredienti di un oggetto sono contenuti nell'insieme degli ingredienti di ogni oggetto che da lui dipende. Come semplice corollario si ha che, inserendo in cache l'oggetto A dell'esempio precedente al posto di A', tutti gli oggetti che dipendono da A' supereranno il type-checking a patto che la regola di conversione ignori gli indici; questo è esattamente ciò che è stato implementato.

5.2.5 CicSubstitution, CicReduction

I moduli CicSubstitution e CicReduction sono stati implementati in maniera naïf, con sostituzioni esplicite. Questo ha permesso al codice di essere estremamente aderente alle definizioni formali, ma rende la whd, ovvero la funzione che restituisce la forma normale di testa debole di un termine, molto inefficiente: per esempio, per calcolare il fattoriale di 6, la nostra implementazione impiega circa 2 minuti contro il secondo richiesto da Coq. Lo scarso utilizzo della riduzione nelle dimostrazioni formali della libreria di Coq⁷, però, annulla l'inefficienza, permettendoci di ottenere buone prestazioni.

La prima implementazione fornita, a dire il vero, era estremamente poco soddisfacente dal punto di vista delle prestazioni. Un attento profiling ha permesso di individuare la sorgente delle inefficienze nell'implementazione della are_convertible, che decide la convertibilità di due termini. In particolare, la funzione veniva richiamata la maggior parte delle volte su termini identici, che venivano visitati interamente in maniera ricorsiva. Una piccola euristica che abbiamo introdotto è il confronto preliminare dei due termini, effettuato utilizzando l'uguaglianza polimorfa di OCaml, la cui implementazione è molto efficiente. I risultati dell'applicazione di questa semplice euristica sono stati stupefacenti: le prestazioni del proof-checking dell'intera libreria standard di Coq sono state incrementate di circa dieci volte.

5.2.6 CicTypeChecker

L'implementazione del type-checker è resa possibile dalla decidibilità delle regole di tipaggio ovvero, in ultima analisi, dalle proprietà di confluenza e normalizzazione forte di CIC. A causa della regola Conv, non è possibile implementare direttamente le regole di tipaggio di CIC come sono state date nel capitolo 2.1. In maniera del tutto standard, viene definita una funzione privata, chiamata type_of, che effettua contemporaneamente sia type-inference che type-checking, verificando tutte le regole diverse dalla Conv e da quelle di introduzione degli oggetti nell'ambiente. Una volta definita la type_of, la verifica di t:T si riduce a quella type_of(t) =_bdi T, ovvero alla are_convertible(type_of(t),T)⁸. Le regole di introduzione degli oggetti nell'ambiente sono implementate seguendo fedelmente le regole date nel paragrafo 2.1.3, fermo restando il meccanismo appena descritto.

Quando, durante il type-checking di un oggetto, si incontra un riferimento ad un oggetto non ancora presente in forma cucinata in cache, si interrompe momentaneamente l'operazione sull'oggetto corrente e si entra in ricorsione su quello riferito, sfruttando i meccanismi messi a disposizione dal modulo CicCache e già descritti nel paragrafo 5.1.4.

5.2.7 Risultati ottenuti

L'implementazione complessiva del proof-checker ha richiesto circa 340 ore uomo; i tre moduli principali (CicSubstitution, CicReduction e CicTypeChecker) sono stati sviluppati lavorando sempre in coppia; i restanti, invece, singolarmente. Complessivamente sono state prodotte circa 3000 righe di codice OCaml, escludendo quelle del metamodulo Getter, ma includendo la nuova implementazione del modulo UriManager. Per effettuare il proof-checking dell'intera libreria standard di Coq vengono richiesti mediamente 5 minuti e 47 secondi, incluso il tempo di parsing che è nell'ordine dei 5 minuti; la prima implementazione richiedeva circa 50 minuti. Non è possibile avere una stima precisa del tempo impiegato da Coq, che è comunque sicuramente inferiore al minuto, parsing incluso⁹. I tempi, comunque, sono inevitabilmente destinati a salire con l'introduzione della gestione del livello degli universi; una prima stima, però, indica che l'incremento dovrebbe essere estremamente contenuto, non superando il minuto.

1: Come conseguenza immediata della regola Ax-Acc si ha Type:Type; in presenza di questa regola è ben nota (vedi [Coq86]) l'inconsistenza del sistema logico, nel quale è possibile codificare un paradosso analogo a quello di Russel.
2: Durante lo sviluppo non è stato in effetti possibile riusare nessuna parte del codice di Coq, principalmente a causa della rappresentazione interna di questo basata sulla codifica di CIC come istanza di un metalinguaggio.
3: Affinché B registri funzioni presso A è necessario che B dipenda staticamente da A.
4: Oltre a quella, già citata, sull'assenza della gestione dei livelli degli universi, che sono espliciti nella sintassi di CIC, impliciti nella rappresentazione XML, ma ancora assenti nella rappresentazione OCaml.
5: Una possibile rappresentazione dell'albero è il DOM, ovvero un API standard definito dal W3C. La natura tipicamente imperativa di questo, però, si armonizza male in un linguaggio con feature imperative, ma spirito funzionale quale OCaml. Pertanto, nessun parser XML per questo linguaggio lo implementa, preferendogli un'API proprietario dalle caratteristiche similari.
6: Almeno nel caso delle costanti, è facile convincersi dell'aciclicità: se questa venisse violata, esisterebbe una catena infinita di d-espansioni; conseguentemente, il sistema non sarebbe fortemente normalizzabile e, pertanto, nemmeno consistente. Nel caso dei tipi mutuamente (co)induttivi, invece, l'argomento è più complesso, ma semplicemente a causa della particolare formulazione di CIC proposta.
7: Esistono due posizioni filosofiche sul ruolo della riduzione nelle dimostrazioni formali. La prima cerca di evitarla il più possibile, in quanto essa nasconde le motivazioni della correttezza delle prove, che vengono basate esclusivamente sulla correttezza delle regole di riduzione, ovvero sulla metateoria. La seconda la accetta sostenendo che, una volta che ci si fidi della metateoria, le prove per riduzione non debbono essere più comprese. Un esempio può chiarire il punto: si voglia provare il teorema 2 + 3 = 3 + 2; una prima prova risulta immediata utilizzando la proprietà commutativa dell'addizione; un metodo alternativo è giustificare l'uguaglianza poiché entrambi i termini riducono a 5 e la riduzione preserva l'uguaglianza di Leibniz: in questo caso, quindi, la prova è immediata per la proprietà riflessiva dell'uguaglianza di Leibniz.
8: È in questo momento che viene utilizzata la regola Conv.
9: Non bisogna dimenticare che il tempo richiesto dal parsing di Coq è estremamente basso in quanto il formato dei file ``.vo'' è binario.