Chapter 1 Introduzione

Nel 1989, Tim Berners Lee, che lavorava al CERN, Ginevra, scrisse una proposta [Ber89] in cui teorizzava la nascita di quello che sarebbe diventato il World Wide Web (WWW). È bene non dimenticare che tale proposta aveva come fine principale quello della diffusione, indicizzazione e facilità di creazione di documenti scientifici.

La successiva, drammatica esplosione del WWW è ormai storia quotidiana. Nonostante il successo ottenuto, però, le idee di Tim Berners Lee sembrano avere dato solo tiepidi risultati proprio nel campo di applicazione a cui erano mirate, ovvero quello della conoscenza scientifica, specie nell'ambito delle scienze esatte. Attualmente, infatti, la maggior parte dei documenti matematici o fisici che si trovano in rete sono disponibili esclusivamente in formati non ipertestuali e non orientati al contenuto (esempio: PostScript) che ne rendono difficoltosa la catalogazione e la ricerca.

In particolare, in ambito matematico, sarebbe auspicabile avere a disposizione larghe librerie di conoscenza (definizioni, teoremi, assiomi) da utilizzare durante lo sviluppo di proprie teorie. Le operazioni di ricerca immaginabili su tali librerie dovrebbero essere estremamente più sofisticate di quelle su documenti generici. Alcuni esempi potrebbero essere:

Ricerca di tutte le teorie riguardanti l'analisi numerica
Ricerca di tutti i teoremi di analisi numerica che utilizzano il lemma di Zorn
Ricerca di tutti i teoremi dei quali una data formula è un'istanza della tesi
Ricerca di tutti i teoremi direttamente applicabili a partire da un dato insieme di ipotesi

I problemi che hanno impedito fino ad ora la creazione di tali librerie sono di due nature distinte:

Problemi ``tecnologici'' legati alla mancanza di formati orientati al contenuto per la codifica di espressioni matematiche.
Problemi ``fondazionali'' e di formalizzazione della matematica (e delle altre scienze esatte)

Nella prossime due sezioni introdurremo ciascuna classe di problemi e le soluzioni attualmente disponibili; successivamente verranno presentati gli obiettivi di questo lavoro e i lavori correlati.

1.1 L'eXtensible Markup Language

Possiamo individuare due tipologie di formati di file: quelli orientati al contenuto e quelli orientati alla presentazione. Nei primi, usualmente proprietari, l'informazione viene memorizzata in maniera strutturata in modo da facilitarne l'elaborazione. Per la resa del documento sono richieste specifiche applicazioni in grado di interpretarne il formato. Al contrario, i formati di file orientati alla presentazione, come HTML e PostScript, mantengono esclusivamente quella parte di informazione utile alla resa dei documenti. La minore espressività rispetto ai formati orientati al contenuto viene ripagata con la possibilità di avere programmi standard (browser) con i quali accedere ad informazioni di natura completamente eterogenea.

Entrambe le soluzioni sono ovviamente insoddisfacenti: i formati orientati al contenuto portano alla proliferazione di software proprietario ed impediscono la creazione di strumenti, come per esempio motori di ricerca, in grado di lavorare in maniera uniforme sui vari documenti. I formati orientati alla presentazione rendono difficoltosa o impossibile la successiva rielaborazione dell'informazione, nonché la sua catalogazione. Ciò nonostante, presentano alcune caratteristiche interessanti, fra cui l'essere standard aperti, che ne facilitano la diffusione e portano allo sviluppo di un gran numero di strumenti software in grado di interoperare esclusivamente grazie all'adozione di un formato comune.

La necessità di dotare i formati orientati al contenuto delle stesse qualità di quelli orientati alla presentazione ha portato all'idea di utilizzare come formati di memorizzazione istanze di uno stesso metalinguaggio: SGML (Standard Generalized Markup Language, [ISO8879]) è un (meta)linguaggio di markup proposto nel 1986 come standard internazionale per la definizione di metodi device-independent e system-independent per la rappresentazione di informazione testuale in formato elettronico. È possibile scrivere un unico parser per tutti i linguaggi non ambigui istanze di SGML, dove ogni istanza è caratterizzata da una propria sintassi (SGML prescrive il formato di descrizione della sintassi, mentre la semantica viene determinata dalle applicazioni).

SGML fu probabilmente in anticipo sui tempi: la scarsità di memoria e di banda forzarono il metalinguaggio a prevedere istanze il più possibile compatte e non ridondanti e questo complica sia la descrizione della loro sintassi, sia l'implementazione dei parser SGML. Una diretta conseguenza fu la scarsa adozione dello standard, anche se talune sue istanze, in primis HTML e DocBook, hanno riscosso notevoli successi.

Il 10 Febbraio 1998, il World Wide Web Consortium¹ (W3C) emana la raccomandazione [W3Ca] in cui viene descritto l'eXtensible Markup Language (XML). XML è un sottoinsieme di SGML, semplificato dalla (presunta) caduta delle motivazioni per le restrizioni sulle dimensioni dei file. In pochi mesi XML è diventato uno standard consolidato e ha dato l'avvio alla definizione, da parte del W3C, di particolari istanze di XML che sono a loro volta standard per l'elaborazione di documenti XML (descrizione di metadati, trasformazioni fra documenti XML, linguaggi di rendering istanze di XML, etc.). L'idea, destinata in pochi anni a modificare radicalmente il WWW, prevede la possibilità di accedere via rete ai documenti XML, nei quali viene mantenuta tutta l'informazione disponibile. Qualora sia richiesta la resa di tale informazione, l'autore fornirà un secondo documento XML con la descrizione della trasformazione da applicare al primo per ottenerne una rappresentazione in un qualche formato di rendering, istanza di XML, la cui semantica sia nota al browser. Per tutte le operazioni diverse dalla resa, come indicizzazioni ed elaborazioni, l'agente potrà operare direttamente sul documento in formato XML, se ne conosce la semantica, e sui metadati ad esso associati, descritti a loro volta in XML.

XML può quindi essere utilizzato proficuamente per il problema che ci interessa, ovvero la codifica di documenti scientifici formali. Inoltre, esiste un linguaggio di rendering, istanza di XML, chiamato Mathematical Markup Language (MathML) [W3Cb], che è una raccomandazione del W3C per la rappresentazione di contenuto scientifico sul WWW. In particolare, MathML ha come oggetto la resa di espressioni matematiche, sia dal punto di vista prettamente visivo (acustico per non vedenti), sia, con diverse limitazioni, da quello contenutistico.

MathML e XML in genere non sono, però, sufficienti alla creazione di librerie matematiche in grado di fornire le funzionalità di accesso auspicate in precedenza. Per esempio, per risolvere query del tipo ``Ricerca tutti i teoremi direttamente applicabili a partire dalle seguenti ipotesi'', è necessario che non solo le espressioni, ma anche le definizioni e le deduzioni matematiche siano codificate in un particolare sistema logico noto all'agente, affinché questo possa controllarne la veridicità o usarle per nuove deduzioni. In altre parole, è necessaria una semantica formale dei ragionamenti matematici. Questa è la materia di studio della Logica Formale e della Teoria delle Dimostrazioni, branche della scienza studiate da matematici e informatici che traggono origine dallo studio degli aspetti fondazionali della matematica stessa e il cui principale risultato pratico consiste nell'implementazione di proof-assistant.

1.2 I Proof-Assistant

MacKenzie in [Mac95] ha tracciato la storia del theorem proving, della quale vengono riportati i momenti salienti nel prossimo paragrafo; seguirà una critica ai proof-assistant attualmente in uso.

1.2.1 La storia del theorem proving

A partire dalla metà degli anni '50, nacque l'idea di utilizzare i computer per l'automazione del ragionamento umano nell'ambito della dimostrazione di teoremi. In particolare i primi sforzi, dovuti a Newell e Simon [NS56], sono mirati all'emulazione del modo di procedere dei matematici: è l'alba dell'intelligenza artificiale. Una seconda corrente di pensiero, peraltro di maggior successo, si sviluppa pochi anni dopo a partire dalle idee introdotte all'inizio del secolo nell'ambito della logica formale ad opera di Frege, Russel e Whitehead. In questo contesto, non ha nessuna rilevanza la somiglianza del modo di procedere dell'uomo con quello della macchina, che può quindi effettuare ricerche più o meno esaustive all'interno del sistema formale. Nonostante i primi successi dovuti a Gilmore [Gil60] e Wang [Wan60], presto fu evidente come l'esplosione combinatorica rendesse la ricerca impraticabile. Il passo successivo, dovuto a Prawitz [Pra60] e Kanger, fu quello di ritardare il più possibile l'istanziazione delle variabili, sostituendole con opportune variabili libere. Questa e altre migliorie si rivelarono comunque insoddisfacenti, spingendo la ricerca verso nuovi approcci.

Le correnti di lavoro appena discusse sono entrambe basate su un meccanismo di ricerca della prova di tipo top-down, che parte dal teorema da dimostrare effettuando una ricostruzione della prova fino a giungere agli assiomi. Nel 1964, Maslow [Mas64] presenta un nuovo metodo, chiamato metodo inverso, per la ricerca di dimostrazioni cut-free nel calcolo dei sequenti. Il vantaggio di questo metodo di tipo bottom-up, che parte dagli assiomi per giungere alla tesi (goal) da provare attraverso l'applicazione dei passi di inferenza, era quello di rendere l'istanziazione meno costosa. Appena un anno dopo, Robinson [Rob65] sviluppa un diverso metodo di tipo bottom-up, chiamato risoluzione, basato sull'unificazione. L'efficacia del nuovo metodo rispetto ai precedenti causò un vero boom nell'ambito dell'authomated theorem proving. Presto si vide che anche la risoluzione risultava insoddisfacente nel contenere l'esplosione combinatorica quando il numero di assiomi e lemmi aumentavano. La delusione, facilmente prevedibile, portò negli anni '70 al quasi totale abbandono di ulteriori ricerche in questo ambito; inoltre, si ebbe la ripresa della mai cessata polemica fra i sostenitori dell'approccio basato sulla logica formale e quelli dell'approccio basato sull'imitazione del ragionamento umano, che accusavano la risoluzione di essere cieca e stupida non sfruttando alcuna conoscenza sul dominio del problema.

Alla fine degli anni '70, l'enfasi si riversò dalla ricerca automatizzata alla verifica della correttezza delle dimostrazioni: nacque il concetto di proof-assistant, ovvero di uno strumento che accompagni l'utente passo passo durante le dimostrazioni, controllandone e garantendone la correttezza. I primi esempi notevoli furono i sistemi del progetto Automath sviluppato da de Brujin [dBr80], nei quali vennero formalizzate parti significative della matematica. Il risultato più famoso è quello raggiunto da Bentham Jutting [Jut94] che riuscí a formalizzare la Grundlagen theory di Landau.

Avendo abbandonato l'obiettivo della ricerca automatica delle prove, che diventa più difficile con l'aumentare dell'espressività della logica, si può aumentare quest'ultima. In particolare, assumono grande risalto sia le logiche costruttive che il problema della rappresentazione delle dimostrazioni, aspetto spesso non considerato nei dimostratori automatici. Per esempio, mentre in quelli basati sull'unificazione ci si limita a verificare la correttezza di un enunciato cercando una confutazione alla sua negazione in una logica non costruttiva, nel sistema Automath si ricorre al l-calcolo per la codifica delle prove, che vengono sviluppate in una logica costruttiva, eventualmente ampliata con l'assioma, classico, (" P.( P® ^) ® P) o uno ad esso equivalente. Il citato l-calcolo, introdotto all'inizio del secolo dal logico Alonzo Church, è un calcolo i cui unici oggetti (termini) sono funzioni. Nel 1958 venne scoperto da Curry un isomorfismo fra la versione tipata del calcolo e il frammento implicativo della logica costruttiva di Brouwer, indipendentemente riscoperto da Howard nel 1968 [GLT89]. L'isomorfismo, noto come corrispondenza di Curry-Howard, mette in relazione i tipi del calcolo con gli enunciati della logica proposizionale e i termini con le prove; alla riduzione nel l-calcolo corrisponde l'eliminazione dei tagli nelle prove. La possibilità di estendere l'isomorfismo a logiche sempre più espressive (calcolo dei predicati, logiche di ordine superiore) e corrispondenti calcoli [Bar92], fanno di questi un prezioso strumento, sul quale si basano nuove applicazioni della logica in ambito informatico, come l'estrazione di programmi dalle corrispondenti prove di correttezza e terminazione [Pau89].

Nel 1972, Robin Milner introduce LCF (Logic for Computable Functions), un proof-assistant interattivo basato sull'isomorfismo di Curry-Howard. Nella successiva versione del 1977, chiamata Edinburgh LCF, viene introdotto un sofisticato e innovativo meccanismo per la definizione di tattiche, basato su un metalinguaggio chiamato ML (Meta Language). Una tattica è una procedura in grado di costruire in maniera top-down il l-termine che prova un goal dati i l-termini che provano nuovi goal proposti dalla tattica. L'architettura di LCF prevedeva un nucleo di modeste dimensioni, chiamato proof-checker, per verificare la correttezza delle prove; in virtù dell'isomorfismo, il proof-checker è un type-checker per i corrispondenti l-termini. Intorno a questo nucleo vengono assemblate le altre funzionalità del proof-assistant: la correttezza dell'implementazione di queste, e in particolare dell'implementazione delle varie tattiche, non influenza quella delle prove, che vengono sempre validate dal proof-checker.

L'architettura di LCF è rimasta pressoché invariata e viene oggi utilizzata dalla maggior parte dei proof-assistant, i quali adottano logiche differenti (e con diversi gradi di espressività) a seconda del compito per i quali sono stati sviluppati. Coq, Lego e Hol sono solo alcuni esempi di proof-assistant attualmente in uso basati sulla medesima architettura.

1.2.2 I moderni proof-assistant

Recentemente sono stati sviluppati svariati proof-assistant, basati su differenti paradigmi logici. A differenza dei primi sistemi che erano tutti general-purpose, oggi esistono strumenti mirati ad una particolare categoria di dimostrazioni, quali quelle per la verifica di sistemi hardware o software, oppure mirati a particolari compiti, quali l'estrazione di codice. Nonostante la relativa diffusione di questi strumenti, essi hanno mancato l'obiettivo della creazione di grosse librerie di conoscenza formalizzata e inoltre l'integrazione con il WWW risulta completamente assente. Le principali cause sono di diversa natura:

Eccessiva difficoltà di scrittura delle dimostrazioni
Eccessiva difficoltà (se non impossibilità) di comprensione delle dimostrazioni
Eccessiva dimensione delle prove
Problemi fondazionali
Problemi di natura notazionale
Problemi tecnologici

Analizziamo separatamente ognuno di questi aspetti:

Difficoltà di scrittura delle dimostrazioni

Il meccanismo della ricerca all'indietro delle prove utilizzando opportune tattiche è quello che si è rivelato più promettente. Ciò nonostante, le prove sviluppate nei sistemi formali tendono ad essere enormi e la procedura di dimostrazione estremamente più puntigliosa di quella normalmente utilizzata nelle prove cartacee. Se questo è accettabile in contesti, come quello della verifica di sistemi hardware, dove i benefici risultati dalla certezza della correttezza di dimostrazioni formali ripagano il tempo e la fatica spesi durante la ricerca della dimostrazione, può non esserlo in generale. Per esempio, almeno fino a quando non saranno disponibili grosse librerie e strumenti di ricerca su di esse, non esistono reali vantaggi per un matematico nell'utilizzo di questi strumenti. Infatti, oggi la quasi totalità degli utilizzatori di questi strumenti sono studiosi di informatica.

Attualmente, non sembrano esserci soluzioni per la difficoltà della scrittura delle dimostrazioni, anche se lo sviluppo di tattiche ancora più sofisticate e quello di grosse librerie di lemmi facilmente consultabili on-line potrebbero alleviare il problema.

Difficoltà o impossibilità di comprensione delle dimostrazioni

Una volta conclusa la ricerca di una prova, all'utente restano due ``oggetti'': il primo è la sequenza di tattiche utilizzate; il secondo è la rappresentazione interna della prova, che assumiamo nella discussione essere l-termini come avviene nei sistemi basati sull'isomorfismo di Curry-Howard. I l-termini sono descrizioni delle prove estremamente dettagliate e fedeli. Il livello di dettaglio, però, è cosí elevato da rendere le prove spesso enormi e illeggibili. Inoltre, solo chi conosce approfonditamente il sistema logico in uso, conoscenza non necessaria per trovare le prove, è in grado di interpretare il l-termine. Per questo motivo, la sequenza delle tattiche usate è usualmente considerata la prova cercata. Ciò nonostante, il contenuto informativo di una tattica dipende dal contesto (goal e ipotesi disponibili) in cui viene invocata. Pertanto, solo ridigitando interattivamente l'intera sequenza è possibile coglierne il significato. Inoltre, non esiste una vera correlazione fra il livello di dettaglio delle tattiche e quello necessario e sufficiente a comprendere una prova: talvolta più tattiche sono necessarie per dimostrare fatti presumibilmente ovvi; altre volte tattiche molto potenti trovano automaticamente dimostrazioni per niente immediate.

Esistono attualmente tre approcci al problema. Il primo prevede lo sviluppo di tattiche sempre più ``naturali'', che corrispondano ai passi logici delle dimostrazioni. Attualmente, questo approccio sembra aver ottenuto solamente un successo molto limitato. Il secondo è l'utilizzo di strumenti automatici in grado di sintetizzare prove in linguaggio pseudo-naturale a partire dai l-termini e/o dalla sequenza di tattiche. Per dimostrazioni non banali, i risultati sono chiaramente insoddisfacenti, con parti della dimostrazione sovradettagliate e altre sottodettagliate, per non citare l'artificialità delle descrizioni, specie in presenza di logiche complesse. Il terzo approccio, adottato dal sistema Mizar², non prevede la ricerca di prove in maniera top-down tramite tattiche; bensí le prove vengono già scritte in linguaggio pseudo-naturale. In effetti, Mizar non si basa sull'isomorfismo di Curry-Howard e utilizza una logica che è molto meno espressiva di quella utilizzata dagli altri proof-assistant³. Ciò nonostante, Mizar è un sistema creato con il preciso intento di raggiungere un certo successo nell'ambiente matematico, che risponde a problemi effettivamente sentiti dai matematici e che non richiede la conoscenza di particolari nozioni per essere utilizzato. Inoltre, nel sistema sono integrate procedure euristiche di ricerca automatica delle prove semplici che permettono di scrivere dimostrazioni spesso allo stesso livello di dettaglio delle corrispondenti prove cartacee. Queste caratteristiche, che ben ripagano la scarsa espressività del sistema logico e la conseguente impossibilità di usarlo, per esempio, per la verifica e l'estrazione da prove di programmi, hanno determinato un enorme successo del sistema: attualmente esistono circa 400 articoli matematici sviluppati in Mizar con più di 20.000 teoremi dimostrati.

Nel corso di questa tesi verrà proposto un ulteriore approccio che vuole essere una sintesi della naturalezza delle prove scritte in Mizar con l'utilizzo di sistemi basati sull'isomorfismo di Curry-Howard.

Dimensione delle prove

I l-termini che rappresentano le prove possono rapidamente diventare enormi, specie quando nelle dimostrazioni è necessario provare uguaglianze e disuguaglianze di espressioni complesse. Talvolta, l'eccessiva dimensione dei termini è dovuta ad ``errori'' non eliminati nel processo di dimostrazione, come vicoli ciechi o inutili espansioni di definizioni. Questi errori, facilmente evitabili, passano spesso inosservati in quanto l'utente non vede, se non su richiesta, il l-termine che viene prodotto automaticamente dall'applicazione delle tattiche. Altre volte, la grandezza delle prove è dovuta alla non disponibilità di lemmi necessari durante la dimostrazione. In questi casi, vi è la tentazione per l'utente a provare l'istanza del lemma direttamente nel corso della dimostrazione, ottenendo una prova che contiene anche quella del lemma. Anche in questo caso è sufficiente prestare attenzione per evitare il problema. Infine, esistono molti altri casi in cui le prove risultano enormi a causa di ridondanze richieste dal sistema logico inevitabili da parte dell'utente [NL98]. Il problema è particolarmente sentito ed è destinato a diventare un importante tema di ricerca nel prossimo futuro.

Problemi fondazionali

Definizioni di uno stesso concetto date all'interno di sistemi formali distinti sono diverse e incompatibili. Per esempio, nonostante Coq e Lego si basino su varianti molto simili dello stesso calcolo, le definizioni date in un sistema non possono essere utilizzate nell'altro. In un certo senso, le definizioni o dimostrazioni in un sistema logico hanno la parvenza di codifiche. Quindi, per poter riutilizzare una definizione data in un altro sistema, l'unico modo è quello di ricodificarla.

È possibile creare procedure automatiche per la conversione fra sistemi logici distinti? La risposta sembra essere affermativa, anche se finora tentativi in questo senso [Har96] hanno raggiunto risultati insoddisfacenti. Il principale problema potrebbe essere costituito dalla differenza fra le definizioni compilate e quelle ``naturali'' che si aspetterebbe l'utente. Per esempio, nei sistemi che prevedono abstract data type (formalismi basati sulla type-theory di Martin-Löf), il tipo dei numeri naturali è un tipo di dato induttivo i cui unici costruttori sono lo zero e l'operatore successore. Nei sistemi basati sulla set-theory, invece, lo zero corrisponde all'insieme vuoto e l'operatore successore è definito a partire dall'unione insiemistica. È sicuramente possibile ``compilare'' la seconda definizione nei sistemi del primo tipo una volta sviluppata una teoria degli insiemi; quella che si ottiene, però, non è certamente la definizione induttiva.

Anche questo problema è particolarmente sentito ed è già un importante tema di ricerca, destinato ad acquisire una sempre maggiore attenzione nel prossimo futuro. Ad accrescerne la difficoltà, contribuiscono problemi tecnologici che attualmente non permettono ai proof-assistant di comunicare fra loro, complicando l'implementazione della traduzione automatica. La risoluzione di questi problemi tecnologici è quindi un risultato importante pienamente raggiunto in questa tesi.

Problemi notazionali

Il fatto che definizioni di uno stesso concetto date all'interno di sistemi formali distinti siano diverse è spesso del tutto irrilevante per l'utente, in particolar modo per quanto riguarda la notazione. Per esempio, indipendentemente dalla particolare codifica della definizione di appartenenza di un elemento x ad un insieme I, si vorrebbe utilizzare la notazione standard x Î I. L'associazione di questa notazione alla definizione, a differenza di quanto si potrebbe pensare, non è banale. In Coq, per esempio, un insieme I di elementi di tipo U è definito come la sua funzione caratteristica di tipo U ® Prop. Pertanto, la notazione x Î I deve essere utilizzata per l'applicazione di I ad x ogni volta che I di tipo U ® Prop è intesa come funzione caratteristica⁴.

Nasce quindi il problema della rimatematizzazione delle definizioni formali, ovvero dell'associazione dell'usuale notazione matematica bidimensionale ai concetti codificati nei sistemi formali. Questo problema è sicuramente centrale nel contesto delle librerie matematiche elettroniche e sarà ampiamente affrontato in questa tesi.

Problemi tecnologici

Gli attuali proof-assistant sono tipici prodotti delle architetture software di tipo application-centric. In queste architetture, ampiamente diffuse fino alla prima metà degli anni '90, l'enfasi è posta sull'applicazione come strumento centralizzato di accesso all'informazione. I dati non sono importanti di per sé, ma esclusivamente perché esiste l'applicazione in grado di compiere elaborazioni su di essi. Per questo motivo, vengono tipicamente utilizzati formati di file proprietari, che vengono cambiati ad ogni versione del programma. Questo comporta che l'unico modo per aggiungere nuovi tipi di elaborazioni sui dati consiste nell'aggiunta di nuove funzionalità all'applicazione. Come conseguenza, i programmi application-centric diventano presto molto complessi da estendere e da usare e presentano molti feature scorrelati fra loro e raramente utilizzati. Infine, quando cessa lo sviluppo dell'applicativo, diventa impossibile accedere a tutta l'informazione contenuta nei file in formato proprietario. Per esempio, tutta la matematica formalizzata nei sistemi Automath è andata completamente perduta.

Dalla metà degli anni '90, sotto la spinta dal successo del WWW, è stato sviluppato un nuovo modello di architettura software, chiamato document-centric o content-centric, che risolve i problemi del modello application-centric. Nel modello content-centric l'enfasi è posta sull'informazione, che deve essere memorizzata in un formato standard, indipendente dall'applicazione e possibilmente estensibile, com'è XML. L'utilizzo di questi formati è sufficiente alle applicazioni per poter interagire fra loro; come conseguenza scompaiono le grandi applicazioni monolitiche, sostituite da programmi cooperanti molto più piccoli e semplici che possono essere scritti da team differenti nel linguaggio di programmazione più adatto al tipo di elaborazione. Quando necessario, architetture più raffinate, tipiche dei sistemi distribuiti, possono essere sfruttate per aumentare il livello di interazione delle diverse applicazioni. L'adozione di XML come meta-formato standard per le architetture content-centric permette, inoltre, lo sviluppo di applicazioni in grado di lavorare in maniera uniforme su tipi di dati eterogenei.

Mentre è in corso di aggiornamento gran parte del software in circolazione per adottare il modello document-centric, il mondo dei proof-assistant, costituito da molti sistemi con ristrette nicchie d'utenza, sembra restare indifferente. Uno degli scopi principali di questa tesi è proprio quello di introdurre in questo mondo il paradigma document-centric, attraverso la creazione di nuovi strumenti e il recupero e la valorizzazione dell'informazione codificata nei sistemi attualmente in uso.

1.3 Il progetto HELM

HELM⁵ (Hypertextual Electronic Library of Mathematics) è un progetto a lungo termine sviluppato presso l'Università di Bologna dal Prof. Andrea Asperti e dal suo gruppo di ricerca⁶. Lo scopo è la progettazione e l'implementazione di strumenti per lo sviluppo e lo sfruttamento di larghe librerie ipertestuali e distribuite di conoscenza matematica formalizzata che comprendano tutto il materiale già codificato nei sistemi attuali. Questa tesi è un resoconto dettagliato delle scelte progettuali ed implementative effettuate nel corso dell'ultimo anno di sviluppo del sistema HELM⁷.

1.3.1 Requisiti di HELM

I principali requisiti del progetto, motivati dalle osservazioni esposte nelle precedenti sezioni, sono:

Utilizzo di formati standard. Tutti i documenti che formano la libreria e i metadati su di essi devono essere descritti in XML. Per le elaborazioni sui documenti devono essere utilizzati, quando possibile, standard già definiti (per esempio, XSLT per le trasformazioni fra file XML).
Distribuzione e replicazione. La libreria deve essere distribuita e, per motivi di efficienza e fault-tolerance, deve prevedere l'esistenza di più copie di uno stesso documento. Per motivi di rilocabilità e bilanciamento del carico, devono essere utilizzati nomi logici per individuare gli elementi della libreria. Conseguentemente, devono essere definiti e realizzati opportuni meccanismi per la risoluzione dei nomi.
Facilità di pubblicazione e accesso. La disponibilità di uno spazio HTTP o FTP deve essere l'unico requisito per poter contribuire alla libreria. In particolare, non si può fare nessuna assunzione sul server utilizzato per la pubblicazione dei documenti, come la possibilità di mandare in esecuzione particolari programmi. Analogamente, per poter consultare la libreria, dovrà essere fornita un'interfaccia Web usufruibile con un comune browser. Interfacce di altro tipo potranno essere fornite per elaborazioni che richiedano una maggiore interattività, come la scrittura di nuovi teoremi.
Modularità. Gli strumenti utilizzati per accedere e contribuire alla libreria dovranno essere il più modulari possibile. In particolare, il livello dell'interazione con l'utente deve essere chiaramente separato da quello dell'elaborazione per permettere l'implementazione di diversi tipi di interfacce (interfacce testuali, grafiche e Web).
Sfruttamento dell'informazione già codificata. Devono essere implementati strumenti che permettano di esportare verso la libreria HELM l'informazione già codificata nei proof-assistant esistenti. Il progetto non ha scopi fondazionali: non si propone un unico formalismo logico in cui codificare tutta la libreria. Al contrario, i formalismi esistenti non devono essere eliminati o modificati, ma standardizzati descrivendoli in formato XML.

1.3.2 Architettura generale di HELM

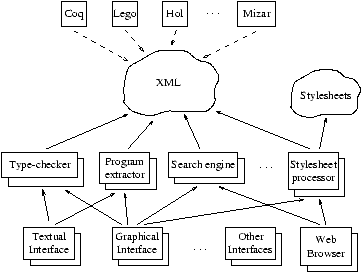
Figura 1.1: Architettura generale del progetto HELM

In figura 1.1 viene brevemente schematizzata l'architettura generale di HELM, che verrà spiegata in dettaglio nei successivi capitoli, in cui verranno motivate le scelte effettuate. La nuvola al centro, etichettata con XML, rappresenta la libreria distribuita di documenti matematici. In alto sono elencati alcuni degli attuali proof-assistant: le linee tratteggiate simboleggiano i meccanismi di esportazione da questi sistemi verso i formati standard usati da HELM. Il primo livello di moduli in basso comprende tool in grado di lavorare sul formato XML, come, per esempio, motori di ricerca. Fra questi, alcuni reimplementano in maniera modulare le funzionalità usualmente presenti nei proof-assistant, come il type-checking o la type-inference.

Una classe importante di tool è quella responsabile della trasformazione dei documenti in un formato di resa appropriato: è durante questa trasformazione che deve avvenire il processo di rimatematizzazione del contenuto, basato sulla scelta, da parte dell'utente, di un'opportuna notazione. In conformità al primo requisito della sezione 1.3.1, l'utente può specificare le notazioni da utilizzare sotto forma di fogli di stile XSLT⁸. Processori XSLT standard possono quindi essere utilizzati per applicare le trasformazioni. I fogli di stile di notazioni matematiche formano una seconda libreria, anch'essa distribuita, rappresentata in figura dalla nuvola etichettata con XSLT.

L'ultimo livello in basso è quello delle interfacce, che verranno costruite assemblando uno o più moduli del livello soprastante, fornendone un accesso uniforme.

1.3.3 Lo sviluppo di HELM

Per il successo del progetto è necessario che la comunità dei proof-assistant contribuisca attivamente alla creazione della libreria e dei tool di gestione. In particolare, è auspicabile che i moduli di esportazione dai sistemi esistenti siano realizzati dai rispettivi autori. Per il momento abbiamo scelto di realizzare noi quello per Coq (vedi capitolo 2), uno dei proof-assistant più avanzati, al fine di esportarne la libreria standard per potere sviluppare e testare le altre componenti del progetto.

Lo sviluppo di HELM è stato articolato in cinque fasi:

Definizione del formato XML per i documenti descritti nel sistema logico di Coq (CIC, Calculus of (Co)Inductive Constructions); progettazione e implementazione del modulo di esportazione da Coq; definizione del modello di distribuzione della libreria e realizzazione dei tool necessari.
Progettazione e realizzazione di un CIC proof-checker per i file della libreria.
Definizione del meccanismo per l'associazione della notazione ai documenti, tramite l'uso di stylesheet; scrittura di stylesheet per i documenti della libreria; implementazione di interfacce, basate sul proof-checker e su processori XSLT standard, per la consultazione della libreria.
Definizione dei metadati associati ai documenti. Implementazione dei meccanismi di indicizzazione e ricerca.
Studio sperimentale di metodi per la rappresentazione delle prove.

Le prime tre fasi sono state affrontate con successo, anche se le relative implementazioni sono da considerarsi esclusivamente prototipi. Le ultime due fasi sono in lavorazione e verranno presumibilmente completate nel corso del 2001.

1.4 Lavori correlati

Il progetto HELM si pone nel punto di intersezione fra gli studi su digital-library, web-publishing e proof-reasoning, presentando numerosi elementi di novità rispetto allo stato dell'arte in ognuno di questi campi. Nel campo delle digital-library, il progetto più affine è EULER⁹. EULER è un progetto co-finanziato dalla Commissione Europea nel settore Telematics for Libraries il cui sviluppo è iniziato nel 1998 e dovrebbe terminare entro il 2001. L'obiettivo di EULER è fornire un servizio per la ricerca di risorse informative sulla matematica quali libri, pre-print, pagine Web, abstract e spogli di articoli e riviste, periodici, rapporti tecnici e tesi. Attraverso l'interfaccia di ricerca di EULER è possibile interrogare simultaneamente un insieme di basi di dati. In particolare, il progetto si propone di integrare i seguenti tipi di risorse documentarie:

Basi di dati bibliografiche
Cataloghi di biblioteche (OPAC)
Riviste elettroniche prodotte da editori accademici
Server di pre-pubblicazioni e letteratura grigia
Indici di risorse matematiche in rete

Queste risorse sono integrate e messe a disposizione per mezzo di un'interfaccia utente WWW comune, il motore di ricerca EULER, e l'uso del protocollo Z39.50 per l'interrogazione simultanea delle diverse basi dati che condividono lo stesso schema basato sullo standard di metadati Dublin Core. La prima differenza rispetto al nostro progetto è che EULER si occupa di tutte le risorse matematiche esistenti, mentre HELM considera esclusivamente i documenti di matematica formale. Inoltre, poiché i documenti indicizzati da EULER sono tipicamente in formati orientati alla rappresentazione, come PostScript o PDF, le modalità di ricerca possibili saranno decisamente inferiori a quelle previste da HELM. È ovviamente possibile e ausplicabile l'aggiunta della libreria di HELM alla lista delle risorse catalogate.

Nell'ambito del web-publishing esistono già due standard per la rappresentazione di documenti matematici. Il primo, MathML, è uno standard del World Wide Web Consortium definito per codificare in XML sia il contenuto che la presentazione di espressioni matematiche. Il suo dominio di applicazione si estende dai sistemi per la computer-algebra al publishing, sia Web che cartaceo. Mentre la parte di MathML che si occupa della presentazione può essere efficacemente utilizzata da HELM, quella che codifica il contenuto non è direttamente fruibile per la memorizzazione di matematica formale per almeno due motivi. Il primo è la natura infinitaria della conoscenza matematica, che non può essere colta da alcun linguaggio mancante della possibilità di definire nuovi concetti. Infatti, MathML si pone l'obiettivo di definire un elemento di markup per quasi ogni operazione o entità matematica che venga studiata nelle scuole americane fino ai primi due anni di college inclusi, il che corrisponde alla conoscenza di uno studente europeo che abbia conseguito un livello A o ``baccalaureate''. Per tutte le altre nozioni matematiche, l'unica possibilità è quella di utilizzare un elemento generico, associandogli uno specifico markup di presentazione ed il URI di un documento, la cui forma non viene specificata, che ne descriva la semantica. Ciò è altamente insufficiente per la codifica di matematica formale, anche se fornisce un interessante linguaggio semi-formale utilizzato proficuamente in HELM durante la fase di rimatematizzazione. La precedente osservazione non si applica alla parte di MathML per la descrizione della presentazione delle espressioni in quanto questa è facilmente codificabile attraverso un numero finito di elementi di markup, come dimostra facilmente il linguaggio di L^AT_EX. Il secondo motivo per cui la parte di MathML per la descrizione del contenuto non è adatta alla codifica della matematica formale, è che ad ogni entità matematica viene associata la sua semantica standard, che non è definita univocamente in un contesto formale. Per esempio, all'uguaglianza di MathML corrispondono nei sistemi formali diverse uguaglianze, come quelle di Leibniz a livello dei termini e dei tipi o quelle estensionale e intensionale per le funzioni. Durante la fase di rimatematizzazione, comunque, è naturale identificarle tutte con l'uguaglianza semi-formale di MathML, a patto che sia possibile risalire alle loro definizioni formali.

Il secondo standard per la codifica del contenuto matematico nell'ambito del web-publishing è OpenMath, che si preoccupa di complementare lo standard MathML definendo una semantica semi-formale per gli elementi contenutistici. L'uso consigliato di OpenMath in ambito MathML è, infatti, quello di fornire il formato dei documenti referenziati da MathML per specificare la semantica per gli elementi contenustici introdotti dagli utenti. Se si è interessati esclusivamente al contenuto, OpenMath può essere utilizzato anche separatamente da MathML. Infatti, l'obiettivo dichiarato di OpenMath è ``la rappresentazione di oggetti matematici con la loro semantica, permettendone lo scambio fra programmi, la memorizzazione in database e la pubblicazione sul WWW''. Concretamente, OpenMath si propone di definire un'architettura per lo scambio di espressioni matematiche basata su tre componenti: i frasari (phrasebook), i dizionari di contenuto (content dictionary, CD) e un formato XML di rappresentazione per questi e per le espressioni matematiche. I frasari sono interfacce software per la codifica di espressioni matematiche dal formato MathML/OpenMath a quello interno delle applicazioni orientate al contenuto, quali tool per la computer algebra come Mathematica, Maple o Derive. I content dictionary sono grandi tabelle, ipoteticamente una per ogni teoria matematica, che associano ad ogni entità (funzione, relazione, insieme) una sua descrizione informale e una ``formale'', costituita dalla sua signature. Per esempio, la descrizione informale della funzione quoziente (quotient), è ``Integer division operator. That is, for integers a and b, quotient denotes q such that a=bq+r, with |r| less than |b| and ar positive.''; la sua signature è il tipo Z × Z ® Z dove Z è l'insieme dei numeri interi. Questo tipo di semantica, che possiamo definire al più semi-formale, è sufficiente per lo scambio di informazione matematica in ambiti dove non si è interessati alle prove, ma esclusivamente alle espressioni; gli obiettivi di HELM sono però molto più ambiziosi e richiedono una semantica formale sia per i tipi che per i corpi delle definizioni. Pertanto, HELM non può beneficiare della semantica di OpenMath. Nonostante questo, è sicuramente utile, ma non ancora implementato, l'utilizzo di OpenMath nella rappresentazione semi-formale in MathML content utilizzata nel progetto HELM.

Nell'ambito dei proof-assistant, esistono due linee di ricerca che hanno affinità con il progetto HELM. La prima è quella delle interfacce grafiche. In questo ambito, l'obiettivo è lo sviluppo di sistemi in ambiente grafico che aiutino l'utente nella visualizzazione e nella ricerca delle dimostrazioni. Si pone una grossa enfasi sul proof-by-clicking, ovvero sulla possibilità di applicare tattiche semplicemente selezionando il termine su cui agire e, per esempio, selezionando il lemma da applicare. Fra l'altro, il proof-by-clicking solleva l'utente dall'onere di memorizzare la sintassi, spesso complicata, del linguaggio delle tattiche dei vari proof-assistant, creando sistemi utilizzabili per interfacciarsi con proof-assistant differenti. Fra questi sistemi ricordiamo Proof General¹⁰, che è sviluppato sotto Emacs e lavora già con diversi proof-assistant fra cui Coq e Lego, e PCoq¹¹ che è un'interfaccia grafica per Coq scritta in Java per motivi di portabilità e finalizzata al proof-by-clicking. Poiché, allo stadio attuale, il progetto HELM non si occupa della ricerca delle dimostrazioni, il confronto può essere effettuato solo nel campo della visualizzazione dei termini e delle prove, dove HELM si propone di raggiungere risultati sicuramente più raffinati.

La seconda linea di ricerca è quella della standardizzazione, a livello tecnologico o fondazionale, dei proof-assistant. In questo ambito sono stati proposti due grossi progetti, QED e MathWeb. QED¹², iniziato nel 1994 con la pubblicazione del QED Manifesto [Har94], persegue, come HELM, il fine della creazione di una grande libreria di documenti matematici formalizzati. Per realizzarla, viene proposto un approccio fondazionale mirato alla codifica del contenuto matematico in una logica, detta root logic, sufficientemente espressiva da rappresentare tutta la conoscenza matematica e, al tempo stesso, prossima alla logica ``informale'' delle dimostrazioni cartacee. Il progetto, a cui contribuiscono in maniera determinante gli autori di Mizar, dopo un primo slancio iniziale¹³ sembra non aver conseguito grossi successi. Il motivo principale è da cercarsi nella difficoltà dell'approccio fondazionale che, sebbene interessante, non permette, almeno per ora, il recupero dell'informazione già codificata in proof-assistant basati su logiche non banali. In mancanza di questo, la proposta si riduce al semplice sviluppo di un nuovo proof-assistant, con in più la complicazione di trovare un largo accordo, sicuramente utopistico, sulla logica da utilizzare come root logic. HELM evita accuratamente di commettere lo stesso errore¹⁴, proponendo prima di tutto una standardizzazione a livello tecnologico, comunque propedeutica a qualsiasi studio fondazionale.

Omega è un grosso progetto intrapreso nel 1994 all'Università di Saarland dal gruppo di ricerca del Prof. Jörg Siekmann per affrontare il delicato tema dell'integrazione fra proof-assistant e theorem-prover. Successivamente, le finalità del progetto sono state estese, portando alla nascita del progetto MathWeb¹⁵; oggi, MathWeb¹⁶ è sicuramente il progetto più simile ad HELM, prevedendo la creazione di una grande libreria distribuita basata su tecnologia XML. Le differenze fra HELM e MathWeb sono comunque molteplici; la loro analisi viene rimandata al paragrafo 8.1 quando HELM sarà già stato descritto in dettaglio.

Nonostante questa tesi sia la prima presentazione esaustiva del progetto HELM, diversi altri lavori sono stati realizzati per descriverne aspetti specifici:

: Studio e progettazione di un modello RDF per biblioteche matematiche elettroniche [Ric99] è uno studio preliminare, risalente al 1999, sulla possibilità di codificare i metadati della libreria di HELM nel formato standard RDF. Nonostante l'architettura di HELM descritta in questo lavoro sia stata pesantemente modificata, la parte di lavoro inerente ai metadati rappresenta un ottimo punto di partenza per le future scelte progettuali.
: Content Centric Logical Environments [APSSa] è una breve introduzione ai benefici che HELM porterà nell'ambito dei proof-assistant.
: Towards a Library of Formal Mathematics [APSSc] presenta l'intero progetto nell'ottica del precedente articolo.
: XML, Stylesheets and the Re-mathematization of Formal Content [APSSd] affronta il problema della rimatematizzazione del contenuto formale.
: Formal Mathematics in MathML [APSSb] è una descrizione di HELM dal punto di vista del web-publishing, incentrato sull'utilizzo di MathML.

1.5 Organizzazione della tesi

Nel capitolo 2 viene introdotto in dettaglio il sistema formale utilizzato dal proof-assistant Coq. Inoltre, viene data una breve descrizione delle funzionalità di questo e un semplice esempio d'uso.

Nel capitolo 3 viene descritto il modulo che è stato implementato per esportare in XML le teorie scritte in Coq. Inoltre, si descrive l'organizzazione che è stata scelta per i file che compongono la libreria di HELM.

Nel capitolo 4 viene presentato il modello di distribuzione adottato.

Il capitolo 5 descrive brevemente l'implementazione di un proof-checker per i file XML che compongono la libreria.

Il capitolo 6 è interamente dedicato alle trasformazioni utilizzate per associare notazioni alle teorie di HELM.

Il capitolo 7 descrive le interfacce messe a disposizione per la consultazione della libreria.

Infine, il capitolo 8 riassume lo stato attuale del progetto e lo confronta dettagliatamente con MathWeb; per concludere, vengono presentati i possibili sviluppi futuri.

Nel resto di questa tesi vengono assunte la conoscenza da parte del lettore delle tecnologie XML e XSLT e una buona preparazione nel campo della logica formale.

1: http://www.w3c.org
2: http://www.mizar.org
3: Il progetto Mizar fu iniziato circa venti anni fa. La scarsità di documentazione, unita all'utilizzo di codice proprietario, può far nascere sospetti sulla correttezza dell'intero sistema.
4: In Coq è naturalmente possibile definire la funzione appartenenza che, presi in input un insieme I e un elemento x, ritorna il risultato dell'applicazione di I ad x. Quindi si può arguire che, se si vuole la notazione x Î I, allora si deve utilizzare la funzione appartenenza. Anche se in linea di principio questo è giusto, si avrebbe un consistente aumento della dimensione delle prove. Inoltre, in presenza di isomorfismi, l'utilizzo di simili artifizi è pratica comunemente accettata in matematica.
5: http://www.cs.unibo.it/helm
6: I membri attuali sono: Prof. Andrea Asperti, Dott. Luca Padovani, Sig. Claudio Sacerdoti Coen e Dott. Irene Schena.
7: L'idea del progetto risale alla fine del 1997. L'autore contribuisce attivamente al suo sviluppo dall'estate del 1999, quando è stata definita l'architettura generale ed è iniziata la fase implementativa.
8: XSLT è lo standard per la descrizione di trasformazioni fra documenti XML. Un foglio di stile è un documento XSLT che definisce un insieme di regole di trasformazione.
9: http://www.emis.de/projects/EULER/
10: http://zermelo.dcs.ed.ac.uk/proofgen
11
12: http://www-unix.mcs.anl.gov/qed
13: Una prima conferenza fu tenuta nel 1994 ad Argonne, seguita da una seconda a Varsavia nel 1995.
14: Vedi il primo requisito del paragrafo 1.3.1.
15: http://www.mathweb.org
16: Con Omega viene ancora indicato il sotto-progetto mirato al raggiungimento degli obiettivi originari.