Università degli Studi di Bologna
Facoltà di Scienze Matematiche, Fisiche e Naturali
Corso di Laurea in Informatica
Materia di Tesi: Linguaggi di programmazione
Progettazione e realizzazione con tecnologia XML di basi distribuite
di conoscenza matematica formalizzata
Tesi di Laurea di:
Claudio Sacerdoti Coen |
|
Relatore:
Chiar.mo Prof. Andrea Asperti |
Parole chiave: Librerie digitali; Matematica formale; XML; MathML; Proof-assistant
II Sessione
Anno Accademico 1999-2000
A Barbara
e alla mia famiglia
Chapter 1 Introduzione
Nel 1989, Tim Berners Lee, che lavorava al CERN, Ginevra, scrisse una
proposta [Ber89] in cui teorizzava la nascita di quello che
sarebbe diventato il World Wide Web (WWW). È bene non dimenticare che tale
proposta aveva come fine principale quello della diffusione, indicizzazione e
facilità di creazione di documenti scientifici.
La successiva, drammatica esplosione del WWW è ormai storia quotidiana.
Nonostante il successo ottenuto, però, le idee di Tim Berners Lee sembrano
avere dato solo tiepidi risultati proprio nel campo di applicazione a cui
erano mirate, ovvero quello della conoscenza scientifica, specie nell'ambito
delle scienze esatte. Attualmente, infatti, la maggior parte dei documenti
matematici o fisici che si trovano in rete sono disponibili esclusivamente
in formati non ipertestuali e non orientati al contenuto (esempio: PostScript)
che ne rendono difficoltosa la catalogazione e la ricerca.
In particolare, in ambito matematico, sarebbe auspicabile avere a disposizione
larghe librerie di conoscenza (definizioni, teoremi, assiomi) da utilizzare
durante lo sviluppo di proprie teorie. Le operazioni di ricerca immaginabili
su tali librerie dovrebbero essere estremamente più sofisticate di quelle
su documenti generici. Alcuni esempi potrebbero essere:
-
Ricerca di tutte le teorie riguardanti l'analisi numerica
- Ricerca di tutti i teoremi di analisi numerica
che utilizzano il lemma di Zorn
- Ricerca di tutti i teoremi dei quali una data formula è un'istanza
della tesi
- Ricerca di tutti i teoremi direttamente applicabili a partire da
un dato insieme di ipotesi
I problemi che hanno impedito fino ad ora la creazione di tali librerie sono
di due nature distinte:
-
Problemi ``tecnologici'' legati alla mancanza di formati orientati
al contenuto per la codifica di espressioni matematiche.
- Problemi ``fondazionali'' e di formalizzazione della matematica (e delle
altre scienze esatte)
Nella prossime due sezioni introdurremo ciascuna classe di
problemi e le soluzioni attualmente disponibili; successivamente
verranno presentati gli obiettivi di questo lavoro e i lavori correlati.
1.1 L'eXtensible Markup Language
Possiamo individuare due tipologie di formati di file: quelli orientati
al contenuto e quelli orientati alla presentazione. Nei primi, usualmente
proprietari, l'informazione viene memorizzata in maniera strutturata in
modo da facilitarne l'elaborazione. Per la resa del documento sono richieste
specifiche applicazioni in grado di interpretarne il formato.
Al contrario, i formati
di file orientati alla presentazione, come HTML e PostScript, mantengono
esclusivamente quella parte di informazione utile alla resa dei documenti.
La minore espressività rispetto ai formati orientati al
contenuto viene ripagata con la possibilità di avere programmi standard
(browser) con i quali accedere ad informazioni di natura completamente
eterogenea.
Entrambe le soluzioni sono ovviamente insoddisfacenti: i formati orientati
al contenuto portano alla proliferazione di software proprietario ed
impediscono la creazione di strumenti, come per esempio motori di ricerca,
in grado di lavorare in maniera uniforme sui vari documenti.
I formati orientati alla presentazione rendono difficoltosa o impossibile
la successiva rielaborazione dell'informazione, nonché la sua catalogazione.
Ciò nonostante, presentano alcune caratteristiche interessanti, fra cui
l'essere standard aperti, che ne facilitano la diffusione e portano allo
sviluppo di un gran numero di strumenti software in grado di
interoperare esclusivamente grazie all'adozione di un formato comune.
La necessità di dotare i formati orientati al contenuto delle stesse
qualità di quelli orientati alla presentazione ha portato all'idea
di utilizzare come formati di memorizzazione istanze di uno stesso
metalinguaggio: SGML (Standard Generalized Markup Language, [ISO8879])
è un (meta)linguaggio di markup proposto nel 1986 come standard
internazionale per la definizione di metodi device-independent e
system-independent per la rappresentazione di informazione testuale
in formato elettronico. È possibile scrivere un unico parser
per tutti i linguaggi non ambigui istanze di SGML, dove
ogni istanza è caratterizzata da una propria sintassi (SGML prescrive il
formato di descrizione della sintassi, mentre la semantica viene
determinata dalle applicazioni).
SGML fu probabilmente in anticipo sui tempi: la scarsità di memoria
e di banda forzarono il metalinguaggio a prevedere
istanze il più possibile compatte e non ridondanti e questo complica
sia la descrizione della loro sintassi, sia l'implementazione dei
parser SGML. Una diretta conseguenza fu la scarsa adozione dello standard,
anche se talune sue istanze, in primis HTML e DocBook, hanno riscosso
notevoli successi.
Il 10 Febbraio 1998, il World Wide Web Consortium1 (W3C)
emana la raccomandazione [W3Ca] in cui viene descritto l'eXtensible Markup
Language (XML). XML è un sottoinsieme di SGML, semplificato dalla (presunta)
caduta delle motivazioni per le restrizioni sulle dimensioni dei file.
In pochi mesi XML è
diventato uno standard consolidato e ha dato l'avvio alla definizione, da
parte del W3C, di particolari istanze di XML che sono a loro volta standard
per l'elaborazione di documenti XML (descrizione di metadati, trasformazioni
fra documenti XML, linguaggi di rendering istanze di XML, etc.).
L'idea, destinata in pochi anni a modificare radicalmente il WWW, prevede
la possibilità di accedere via rete ai documenti XML, nei quali viene
mantenuta tutta l'informazione disponibile.
Qualora sia richiesta la resa di tale informazione, l'autore fornirà
un secondo documento XML con la descrizione della trasformazione da applicare
al primo per ottenerne una rappresentazione in un qualche formato di
rendering, istanza di XML, la cui semantica sia nota al browser. Per tutte le
operazioni diverse dalla resa, come indicizzazioni ed elaborazioni, l'agente
potrà operare direttamente sul documento in formato XML, se ne conosce la
semantica, e sui metadati ad esso associati, descritti a loro volta in XML.
XML può quindi essere utilizzato proficuamente per il problema che ci
interessa, ovvero la codifica di documenti scientifici formali. Inoltre,
esiste un linguaggio di rendering, istanza di XML, chiamato Mathematical
Markup Language (MathML) [W3Cb], che è una raccomandazione del W3C
per la rappresentazione di contenuto scientifico sul WWW. In particolare,
MathML ha come oggetto la resa di espressioni matematiche, sia dal punto
di vista prettamente visivo (acustico per non vedenti), sia, con
diverse limitazioni, da quello contenutistico.
MathML e XML in genere non sono, però, sufficienti alla creazione di
librerie matematiche in grado di fornire le funzionalità di accesso
auspicate in precedenza. Per esempio, per risolvere query del tipo
``Ricerca tutti i teoremi direttamente applicabili a partire dalle
seguenti ipotesi'', è necessario che non solo le espressioni, ma anche
le definizioni e le deduzioni matematiche siano codificate in un particolare
sistema logico noto all'agente, affinché questo possa controllarne la
veridicità o usarle per nuove deduzioni. In altre parole, è necessaria
una semantica formale dei ragionamenti matematici. Questa è
la materia di studio della Logica Formale e della
Teoria delle Dimostrazioni, branche
della scienza studiate da matematici e informatici che traggono origine dallo
studio degli aspetti fondazionali della matematica stessa e il cui principale
risultato pratico consiste nell'implementazione di proof-assistant.
1.2 I Proof-Assistant
MacKenzie in [Mac95] ha tracciato la storia del
theorem proving,
della quale vengono riportati i momenti salienti nel prossimo paragrafo;
seguirà una critica ai proof-assistant attualmente in uso.
1.2.1 La storia del theorem proving
A partire dalla metà degli anni '50, nacque l'idea di utilizzare i
computer per l'automazione del ragionamento umano nell'ambito della
dimostrazione di teoremi. In particolare i primi sforzi, dovuti a Newell
e Simon [NS56], sono mirati all'emulazione del modo di procedere
dei matematici: è l'alba dell'intelligenza artificiale.
Una seconda corrente di pensiero, peraltro di maggior
successo, si sviluppa pochi anni dopo a partire dalle idee introdotte
all'inizio del secolo nell'ambito della logica formale ad opera di
Frege, Russel e Whitehead. In questo contesto, non ha nessuna rilevanza
la somiglianza del modo di procedere dell'uomo con quello della macchina,
che può quindi effettuare ricerche più o meno esaustive all'interno
del sistema formale. Nonostante i primi successi dovuti a Gilmore [Gil60]
e Wang [Wan60], presto fu evidente come l'esplosione combinatorica
rendesse la ricerca impraticabile. Il passo successivo, dovuto a Prawitz
[Pra60] e Kanger, fu quello di ritardare il più possibile
l'istanziazione delle variabili, sostituendole con opportune variabili libere.
Questa e altre migliorie si rivelarono comunque insoddisfacenti, spingendo
la ricerca verso nuovi approcci.
Le correnti di lavoro appena discusse sono entrambe basate su un meccanismo
di ricerca della prova di tipo top-down, che parte dal teorema da dimostrare
effettuando una ricostruzione della prova fino a giungere agli assiomi.
Nel 1964, Maslow [Mas64] presenta un nuovo metodo, chiamato
metodo inverso, per la ricerca di dimostrazioni cut-free nel
calcolo dei sequenti. Il vantaggio di questo metodo di tipo bottom-up,
che parte dagli assiomi per giungere alla tesi (goal) da provare attraverso
l'applicazione dei passi di inferenza, era quello di rendere l'istanziazione
meno costosa. Appena un anno dopo, Robinson [Rob65] sviluppa un
diverso metodo di tipo bottom-up, chiamato risoluzione, basato
sull'unificazione. L'efficacia del nuovo metodo rispetto ai precedenti
causò un vero boom nell'ambito dell'authomated theorem proving.
Presto si vide che anche la risoluzione risultava insoddisfacente
nel contenere l'esplosione combinatorica quando il numero di assiomi
e lemmi aumentavano. La delusione, facilmente prevedibile, portò negli
anni '70 al quasi totale abbandono di ulteriori ricerche in questo ambito;
inoltre, si ebbe la ripresa della
mai cessata polemica fra i sostenitori dell'approccio basato sulla logica
formale e quelli dell'approccio basato sull'imitazione
del ragionamento umano, che accusavano la risoluzione di essere cieca e
stupida non sfruttando alcuna conoscenza sul dominio del problema.
Alla fine degli anni '70, l'enfasi si riversò dalla ricerca automatizzata
alla verifica della correttezza delle dimostrazioni: nacque il concetto
di proof-assistant, ovvero di uno strumento che accompagni
l'utente passo passo durante le dimostrazioni, controllandone e garantendone
la correttezza.
I primi esempi notevoli furono i sistemi del progetto Automath sviluppato
da de Brujin [dBr80], nei quali vennero formalizzate parti significative
della matematica. Il risultato più famoso
è quello raggiunto da Bentham Jutting [Jut94] che riuscí a
formalizzare la Grundlagen theory di Landau.
Avendo abbandonato l'obiettivo della ricerca automatica delle prove,
che diventa più difficile con l'aumentare dell'espressività della logica,
si può aumentare quest'ultima. In particolare, assumono grande
risalto sia le logiche costruttive che
il problema della rappresentazione delle dimostrazioni, aspetto spesso
non considerato nei dimostratori automatici. Per esempio, mentre in quelli
basati sull'unificazione ci si limita a verificare la correttezza di un
enunciato cercando una confutazione alla sua negazione in una logica non
costruttiva, nel sistema Automath si ricorre al l-calcolo per la
codifica delle prove, che vengono sviluppate in una logica costruttiva,
eventualmente ampliata con l'assioma, classico,
(" P.( P® ^) ® P) o uno ad esso equivalente.
Il citato l-calcolo, introdotto all'inizio del secolo dal logico Alonzo
Church, è un calcolo i cui unici oggetti (termini) sono funzioni. Nel 1958
venne scoperto da Curry un isomorfismo fra la versione tipata del
calcolo e il frammento implicativo della logica costruttiva di Brouwer,
indipendentemente riscoperto da Howard nel 1968 [GLT89].
L'isomorfismo, noto come corrispondenza di Curry-Howard, mette in
relazione i tipi del calcolo con gli enunciati della logica proposizionale
e i termini con le prove; alla riduzione nel l-calcolo corrisponde
l'eliminazione dei tagli nelle prove. La possibilità di estendere
l'isomorfismo a logiche sempre più espressive (calcolo dei predicati,
logiche di ordine superiore) e corrispondenti calcoli [Bar92],
fanno di questi un prezioso strumento, sul quale si basano nuove applicazioni
della logica in ambito informatico, come l'estrazione di programmi dalle
corrispondenti prove di correttezza e terminazione [Pau89].
Nel 1972, Robin Milner introduce LCF (Logic for Computable Functions),
un proof-assistant interattivo basato sull'isomorfismo di Curry-Howard.
Nella successiva versione del 1977, chiamata Edinburgh LCF,
viene introdotto un sofisticato e innovativo meccanismo per la definizione di
tattiche, basato su un metalinguaggio chiamato ML (Meta Language).
Una tattica è una procedura in grado di costruire in maniera top-down
il l-termine che prova un goal dati i l-termini che provano
nuovi goal proposti dalla tattica.
L'architettura di LCF prevedeva
un nucleo di modeste dimensioni, chiamato proof-checker, per verificare
la correttezza delle prove; in virtù dell'isomorfismo, il proof-checker
è un type-checker per i corrispondenti l-termini. Intorno a questo nucleo
vengono assemblate le altre funzionalità del proof-assistant: la correttezza
dell'implementazione di queste, e in particolare dell'implementazione delle
varie tattiche, non influenza quella delle prove, che vengono sempre validate
dal proof-checker.
L'architettura di LCF è rimasta pressoché invariata
e viene oggi utilizzata dalla maggior parte dei proof-assistant, i quali
adottano logiche differenti (e con diversi gradi di espressività) a seconda
del compito per i quali sono stati sviluppati. Coq, Lego e Hol sono solo
alcuni esempi di proof-assistant attualmente in uso basati sulla medesima
architettura.
1.2.2 I moderni proof-assistant
Recentemente sono stati sviluppati svariati proof-assistant,
basati su differenti paradigmi logici. A differenza dei primi
sistemi che erano tutti general-purpose, oggi esistono
strumenti mirati ad una particolare categoria di dimostrazioni,
quali quelle per la verifica di sistemi hardware o software, oppure
mirati a particolari compiti, quali l'estrazione di codice. Nonostante
la relativa diffusione di questi strumenti, essi hanno mancato
l'obiettivo della creazione di grosse librerie di conoscenza formalizzata
e inoltre l'integrazione con il WWW risulta completamente assente.
Le principali cause sono di diversa natura:
-
Eccessiva difficoltà di scrittura delle dimostrazioni
- Eccessiva difficoltà (se non impossibilità) di comprensione delle
dimostrazioni
- Eccessiva dimensione delle prove
- Problemi fondazionali
- Problemi di natura notazionale
- Problemi tecnologici
Analizziamo separatamente ognuno di questi aspetti:
Difficoltà di scrittura delle dimostrazioni
Il meccanismo della ricerca all'indietro delle prove utilizzando opportune
tattiche è quello che si è rivelato più promettente. Ciò nonostante,
le prove sviluppate nei sistemi formali tendono ad essere enormi e la
procedura di dimostrazione estremamente più puntigliosa di quella normalmente
utilizzata nelle prove cartacee. Se questo è accettabile in contesti, come
quello della verifica di sistemi hardware, dove i benefici risultati dalla
certezza della correttezza di dimostrazioni formali ripagano il tempo e la
fatica spesi durante la ricerca della dimostrazione, può non esserlo in
generale. Per esempio, almeno fino a quando non saranno disponibili grosse
librerie e strumenti di ricerca su di esse, non esistono reali vantaggi per
un matematico nell'utilizzo di questi strumenti. Infatti, oggi la quasi
totalità degli utilizzatori di questi strumenti sono studiosi di informatica.
Attualmente, non sembrano esserci soluzioni per la difficoltà della scrittura
delle dimostrazioni, anche se lo sviluppo di tattiche ancora più sofisticate
e quello di grosse librerie di lemmi facilmente consultabili on-line potrebbero
alleviare il problema.
Difficoltà o impossibilità di comprensione delle dimostrazioni
Una volta conclusa la ricerca di una prova, all'utente restano due ``oggetti'':
il primo è la sequenza di tattiche utilizzate; il secondo è la
rappresentazione interna della prova, che assumiamo nella discussione
essere l-termini come avviene nei sistemi basati sull'isomorfismo di
Curry-Howard. I l-termini sono descrizioni delle prove estremamente
dettagliate e fedeli. Il livello di dettaglio, però, è cosí elevato
da rendere le prove spesso enormi e illeggibili. Inoltre, solo
chi conosce approfonditamente il sistema logico in uso, conoscenza non
necessaria per trovare le prove, è in grado di interpretare il
l-termine.
Per questo motivo, la sequenza delle tattiche usate è usualmente considerata
la prova cercata. Ciò nonostante, il contenuto informativo di una tattica
dipende dal contesto (goal e ipotesi disponibili) in cui viene invocata.
Pertanto, solo ridigitando interattivamente l'intera sequenza è possibile
coglierne il significato. Inoltre, non esiste una vera correlazione fra
il livello di dettaglio delle tattiche e quello necessario e sufficiente
a comprendere una prova: talvolta più tattiche sono necessarie per
dimostrare fatti presumibilmente ovvi; altre volte tattiche molto potenti
trovano automaticamente dimostrazioni per niente immediate.
Esistono attualmente tre approcci al problema.
Il primo prevede lo sviluppo di tattiche sempre più ``naturali'', che
corrispondano ai passi logici delle dimostrazioni. Attualmente, questo
approccio sembra aver ottenuto solamente un successo molto limitato. Il
secondo è l'utilizzo
di strumenti automatici in grado di sintetizzare prove in linguaggio
pseudo-naturale a partire dai l-termini e/o dalla sequenza di tattiche.
Per dimostrazioni non banali, i risultati sono chiaramente insoddisfacenti,
con parti della dimostrazione sovradettagliate e altre sottodettagliate,
per non citare l'artificialità delle descrizioni, specie in presenza
di logiche complesse. Il terzo approccio, adottato dal sistema
Mizar2,
non prevede la ricerca di prove in maniera top-down tramite tattiche;
bensí le prove vengono già scritte in linguaggio pseudo-naturale.
In effetti, Mizar non si basa sull'isomorfismo di Curry-Howard e utilizza una
logica che è molto meno espressiva di quella utilizzata
dagli altri proof-assistant3.
Ciò nonostante, Mizar è un sistema creato con il preciso intento di
raggiungere un certo successo nell'ambiente matematico, che risponde a
problemi effettivamente sentiti dai matematici e che non richiede la
conoscenza di particolari nozioni per essere utilizzato. Inoltre, nel
sistema sono integrate procedure euristiche di ricerca automatica delle prove
semplici che permettono di scrivere dimostrazioni spesso allo stesso livello
di dettaglio delle corrispondenti prove cartacee. Queste caratteristiche,
che ben ripagano la scarsa espressività del sistema logico e la conseguente
impossibilità di usarlo, per esempio, per la verifica e l'estrazione da
prove di programmi, hanno determinato un enorme successo del sistema:
attualmente esistono circa 400 articoli matematici sviluppati in Mizar
con più di 20.000 teoremi dimostrati.
Nel corso di questa tesi verrà proposto un ulteriore approccio che vuole
essere una sintesi della naturalezza delle prove scritte in Mizar con
l'utilizzo di sistemi basati sull'isomorfismo di Curry-Howard.
Dimensione delle prove
I l-termini che rappresentano le prove possono rapidamente diventare
enormi, specie quando nelle dimostrazioni è necessario provare
uguaglianze e disuguaglianze di espressioni complesse. Talvolta, l'eccessiva
dimensione dei termini è dovuta ad ``errori'' non eliminati nel processo di
dimostrazione, come vicoli ciechi o inutili espansioni di definizioni. Questi
errori, facilmente evitabili, passano spesso inosservati in quanto l'utente
non vede, se non su richiesta, il l-termine che viene prodotto
automaticamente dall'applicazione delle tattiche. Altre volte, la grandezza
delle prove è dovuta alla non disponibilità di lemmi necessari durante la
dimostrazione. In questi casi, vi è la tentazione per l'utente a provare
l'istanza del lemma direttamente nel corso della dimostrazione, ottenendo una
prova
che contiene anche quella del lemma. Anche in questo caso è sufficiente
prestare attenzione per evitare il problema. Infine, esistono molti altri
casi in cui le prove risultano enormi a causa di ridondanze richieste dal
sistema logico inevitabili da parte dell'utente [NL98].
Il problema è particolarmente sentito ed è destinato a diventare un
importante tema di ricerca nel prossimo futuro.
Problemi fondazionali
Definizioni di uno stesso concetto date all'interno di sistemi
formali distinti sono diverse e incompatibili. Per esempio, nonostante
Coq e Lego si basino su varianti molto simili dello stesso calcolo,
le definizioni date in un sistema non possono essere utilizzate nell'altro.
In un certo senso, le definizioni o dimostrazioni in un sistema logico
hanno la parvenza di codifiche. Quindi, per poter riutilizzare una definizione
data in un altro sistema, l'unico modo è quello di ricodificarla.
È possibile creare procedure automatiche per la conversione fra sistemi
logici distinti? La risposta sembra essere affermativa, anche se
finora tentativi in questo senso [Har96] hanno raggiunto
risultati insoddisfacenti. Il principale problema potrebbe
essere costituito dalla differenza fra le definizioni compilate e quelle
``naturali'' che si aspetterebbe l'utente. Per esempio, nei sistemi
che prevedono abstract data type (formalismi basati sulla type-theory di
Martin-Löf), il tipo dei numeri naturali è un tipo di dato induttivo
i cui unici costruttori sono lo zero e l'operatore successore. Nei sistemi
basati sulla set-theory, invece, lo zero corrisponde all'insieme vuoto e
l'operatore successore è definito a partire dall'unione insiemistica.
È sicuramente possibile ``compilare'' la seconda definizione nei sistemi
del primo tipo una volta sviluppata una teoria degli insiemi; quella che
si ottiene, però, non è certamente la definizione induttiva.
Anche questo problema è particolarmente sentito ed è già un
importante tema di ricerca, destinato ad acquisire una sempre maggiore
attenzione nel prossimo futuro. Ad accrescerne la difficoltà,
contribuiscono problemi tecnologici che attualmente non permettono
ai proof-assistant di comunicare fra loro, complicando l'implementazione
della traduzione automatica. La risoluzione di questi problemi tecnologici
è quindi un risultato importante pienamente raggiunto in questa tesi.
Problemi notazionali
Il fatto che definizioni di uno stesso concetto date all'interno di
sistemi formali distinti siano diverse è spesso del tutto irrilevante
per l'utente, in particolar modo per quanto riguarda la notazione.
Per esempio, indipendentemente dalla particolare codifica della definizione di
appartenenza di un elemento x ad un insieme I, si vorrebbe utilizzare
la notazione standard x Î I. L'associazione di questa notazione alla
definizione, a differenza di quanto si potrebbe pensare, non è banale.
In Coq, per esempio, un insieme I di elementi di tipo U è definito
come la sua funzione caratteristica di tipo U ® Prop.
Pertanto, la notazione x Î I deve essere utilizzata per l'applicazione
di I ad x ogni volta che I di tipo U ® Prop è
intesa come funzione caratteristica4.
Nasce quindi il problema della rimatematizzazione delle definizioni
formali, ovvero dell'associazione dell'usuale notazione matematica
bidimensionale ai concetti codificati nei sistemi formali. Questo problema è
sicuramente centrale nel contesto delle librerie matematiche elettroniche e
sarà ampiamente affrontato in questa tesi.
Problemi tecnologici
Gli attuali proof-assistant sono tipici prodotti delle architetture software
di tipo application-centric. In queste architetture, ampiamente
diffuse fino alla prima metà degli anni '90, l'enfasi
è posta sull'applicazione come strumento centralizzato di accesso
all'informazione. I dati non sono importanti di per sé, ma esclusivamente
perché esiste l'applicazione in grado di compiere elaborazioni su di essi.
Per questo motivo, vengono tipicamente utilizzati formati di file proprietari,
che vengono cambiati ad ogni versione del programma. Questo comporta che
l'unico modo per aggiungere nuovi tipi di elaborazioni sui dati consiste
nell'aggiunta di nuove funzionalità all'applicazione. Come conseguenza, i
programmi application-centric diventano presto molto complessi da estendere e
da usare e presentano molti feature scorrelati fra loro e raramente
utilizzati. Infine, quando cessa lo sviluppo dell'applicativo, diventa
impossibile accedere a tutta l'informazione contenuta nei file in formato
proprietario. Per esempio, tutta la matematica formalizzata nei sistemi
Automath è andata completamente perduta.
Dalla metà degli anni '90, sotto la spinta dal successo del WWW,
è stato sviluppato un nuovo modello di architettura
software, chiamato document-centric o content-centric,
che risolve i problemi del modello
application-centric. Nel modello content-centric l'enfasi è posta
sull'informazione, che deve essere memorizzata in un formato standard,
indipendente dall'applicazione e possibilmente estensibile, com'è XML.
L'utilizzo di questi formati è sufficiente alle applicazioni per poter
interagire fra loro; come conseguenza scompaiono le grandi applicazioni
monolitiche, sostituite da programmi cooperanti molto più piccoli e semplici
che possono essere scritti da team differenti nel linguaggio di programmazione
più adatto al tipo di elaborazione. Quando necessario, architetture più
raffinate, tipiche dei sistemi distribuiti, possono essere sfruttate per
aumentare il livello di interazione delle diverse applicazioni. L'adozione di
XML come meta-formato standard per le architetture content-centric
permette, inoltre, lo sviluppo di applicazioni
in grado di lavorare in maniera uniforme su tipi di dati eterogenei.
Mentre è in corso di aggiornamento gran parte del software in circolazione per
adottare il modello document-centric, il mondo dei proof-assistant, costituito
da molti sistemi con ristrette nicchie d'utenza, sembra restare indifferente.
Uno degli scopi principali di questa tesi è proprio quello di introdurre in
questo mondo il paradigma document-centric, attraverso la creazione di nuovi
strumenti e il recupero e la valorizzazione dell'informazione codificata
nei sistemi attualmente in uso.
1.3 Il progetto HELM
HELM5
(Hypertextual Electronic Library of Mathematics) è un progetto a lungo
termine sviluppato presso l'Università di Bologna dal Prof. Andrea Asperti
e dal suo gruppo di ricerca6.
Lo scopo è la progettazione e
l'implementazione di strumenti per lo sviluppo e lo sfruttamento di larghe
librerie ipertestuali e distribuite di conoscenza matematica formalizzata che
comprendano tutto il materiale già codificato nei sistemi attuali.
Questa tesi è un resoconto dettagliato delle scelte progettuali ed
implementative effettuate nel corso dell'ultimo anno di sviluppo
del sistema HELM7.
1.3.1 Requisiti di HELM
I principali requisiti del progetto, motivati dalle osservazioni esposte
nelle precedenti sezioni, sono:
-
Utilizzo di formati standard. Tutti i documenti che
formano la libreria e i metadati su di essi devono essere descritti in XML.
Per le elaborazioni sui documenti devono essere utilizzati,
quando possibile, standard già definiti (per esempio, XSLT per le
trasformazioni fra file XML).
- Distribuzione e replicazione. La libreria deve essere
distribuita e, per motivi di efficienza e fault-tolerance, deve prevedere
l'esistenza di più copie di uno stesso documento. Per motivi di
rilocabilità e bilanciamento del carico, devono essere utilizzati nomi
logici per individuare gli elementi della libreria.
Conseguentemente, devono essere definiti e realizzati opportuni meccanismi
per la risoluzione dei nomi.
- Facilità di pubblicazione e accesso. La disponibilità
di uno spazio HTTP o FTP deve essere l'unico requisito per poter contribuire
alla libreria. In particolare, non si può fare nessuna assunzione
sul server utilizzato per la pubblicazione dei documenti,
come la possibilità di mandare in esecuzione particolari programmi.
Analogamente, per poter consultare la
libreria, dovrà essere fornita un'interfaccia Web usufruibile con un
comune browser. Interfacce di altro tipo potranno essere fornite per
elaborazioni che richiedano una maggiore interattività, come la
scrittura di nuovi teoremi.
- Modularità. Gli strumenti utilizzati per accedere e contribuire
alla libreria dovranno essere il più modulari possibile. In particolare,
il livello dell'interazione con l'utente deve essere chiaramente
separato da quello dell'elaborazione per permettere l'implementazione di
diversi tipi di interfacce (interfacce testuali, grafiche e Web).
- Sfruttamento dell'informazione già codificata. Devono essere
implementati strumenti che permettano di esportare verso la libreria
HELM l'informazione già codificata nei proof-assistant esistenti.
Il progetto non ha scopi fondazionali: non si propone
un unico formalismo logico in cui codificare tutta la libreria.
Al contrario, i formalismi esistenti non devono essere eliminati o modificati,
ma standardizzati descrivendoli in formato XML.
1.3.2 Architettura generale di HELM
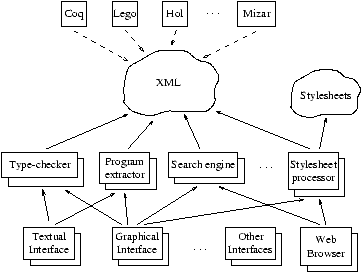
Figura 1.1: Architettura generale del progetto HELM
In figura 1.1 viene brevemente schematizzata
l'architettura generale di HELM, che verrà spiegata in dettaglio nei
successivi capitoli, in cui verranno motivate le scelte effettuate.
La nuvola al centro, etichettata con XML, rappresenta la libreria distribuita
di documenti matematici. In alto sono elencati alcuni degli attuali
proof-assistant: le linee tratteggiate simboleggiano i meccanismi di
esportazione da questi sistemi verso i formati standard usati da HELM.
Il primo livello di moduli in basso comprende tool in grado di lavorare
sul formato XML, come, per esempio, motori di ricerca. Fra questi, alcuni
reimplementano in maniera modulare le funzionalità usualmente presenti
nei proof-assistant, come il type-checking o la type-inference.
Una classe importante di tool è quella responsabile della trasformazione dei
documenti in un formato di resa appropriato: è durante questa trasformazione
che deve avvenire il processo di rimatematizzazione del contenuto, basato
sulla scelta, da parte dell'utente, di un'opportuna notazione. In conformità
al primo requisito della sezione 1.3.1, l'utente
può specificare le notazioni da utilizzare sotto forma di fogli di stile
XSLT8. Processori XSLT standard
possono quindi essere utilizzati per applicare le trasformazioni. I fogli
di stile di notazioni matematiche formano una seconda libreria, anch'essa
distribuita, rappresentata in figura dalla nuvola etichettata con XSLT.
L'ultimo livello in basso è quello delle interfacce, che verranno costruite
assemblando uno o più moduli del livello soprastante, fornendone
un accesso uniforme.
1.3.3 Lo sviluppo di HELM
Per il successo del progetto è necessario che la comunità dei
proof-assistant contribuisca attivamente alla creazione della libreria
e dei tool di gestione. In particolare, è auspicabile che i moduli di
esportazione dai sistemi esistenti siano realizzati dai rispettivi autori.
Per il momento abbiamo scelto di realizzare noi quello per Coq (vedi capitolo
2), uno dei proof-assistant più avanzati, al fine di esportarne la
libreria standard per potere sviluppare e testare le altre componenti del
progetto.
Lo sviluppo di HELM è stato articolato in cinque fasi:
-
Definizione del formato XML per i documenti descritti nel sistema
logico di Coq (CIC, Calculus of (Co)Inductive Constructions);
progettazione e implementazione del modulo di esportazione da Coq;
definizione del modello di distribuzione della libreria e realizzazione
dei tool necessari.
- Progettazione e realizzazione di un CIC proof-checker per i file della
libreria.
- Definizione del meccanismo per l'associazione della notazione ai
documenti, tramite l'uso di stylesheet; scrittura di stylesheet per i
documenti della libreria; implementazione di interfacce, basate sul
proof-checker e su processori XSLT standard, per la consultazione della
libreria.
- Definizione dei metadati associati ai documenti.
Implementazione dei meccanismi di indicizzazione e ricerca.
- Studio sperimentale di metodi per la rappresentazione delle prove.
Le prime tre fasi sono state affrontate con successo, anche se le relative
implementazioni sono da considerarsi esclusivamente prototipi. Le ultime due
fasi sono in lavorazione e verranno presumibilmente completate nel corso
del 2001.
1.4 Lavori correlati
Il progetto HELM si pone nel punto di intersezione fra gli studi su
digital-library,
web-publishing e proof-reasoning, presentando numerosi elementi di novità
rispetto allo stato dell'arte in ognuno di questi campi. Nel campo delle
digital-library, il progetto più affine è
EULER9.
EULER è
un progetto co-finanziato dalla Commissione Europea nel settore
Telematics for Libraries il cui sviluppo è iniziato nel 1998 e dovrebbe
terminare entro il 2001. L'obiettivo di EULER è fornire un
servizio per la ricerca di risorse informative sulla matematica quali libri,
pre-print, pagine Web, abstract e spogli di articoli e riviste, periodici,
rapporti tecnici e tesi. Attraverso l'interfaccia di ricerca di EULER è
possibile interrogare simultaneamente un insieme di basi di dati.
In particolare,
il progetto si propone di integrare i seguenti tipi di risorse documentarie:
-
Basi di dati bibliografiche
- Cataloghi di biblioteche (OPAC)
- Riviste elettroniche prodotte da editori accademici
- Server di pre-pubblicazioni e letteratura grigia
- Indici di risorse matematiche in rete
Queste risorse sono integrate e messe a disposizione per mezzo di
un'interfaccia utente WWW comune, il motore di ricerca EULER, e l'uso
del protocollo Z39.50 per l'interrogazione simultanea delle diverse basi dati
che condividono lo stesso schema basato sullo standard di metadati Dublin Core.
La prima differenza rispetto al nostro progetto è che
EULER si occupa di tutte le risorse matematiche esistenti, mentre
HELM considera esclusivamente i documenti di matematica formale.
Inoltre, poiché i documenti indicizzati da EULER sono tipicamente in formati
orientati alla rappresentazione, come PostScript o PDF, le modalità di
ricerca possibili saranno decisamente inferiori a quelle previste da HELM.
È ovviamente possibile e ausplicabile l'aggiunta della libreria di HELM
alla lista delle risorse catalogate.
Nell'ambito del web-publishing esistono già due standard per la
rappresentazione di documenti matematici. Il primo, MathML, è uno
standard del World Wide Web Consortium definito per codificare in XML
sia il contenuto che la presentazione di espressioni matematiche.
Il suo dominio di applicazione si estende dai sistemi per la computer-algebra
al publishing, sia Web che cartaceo. Mentre la parte di MathML che si occupa
della presentazione può essere efficacemente utilizzata da HELM, quella che
codifica il contenuto non è direttamente fruibile per la memorizzazione di
matematica formale per almeno due motivi. Il primo è la natura infinitaria
della conoscenza matematica, che non può essere colta da alcun linguaggio
mancante della possibilità di definire nuovi concetti.
Infatti, MathML si pone l'obiettivo di definire un elemento di markup per
quasi ogni operazione o entità matematica che venga studiata nelle scuole
americane fino ai primi due anni di college inclusi, il che corrisponde
alla conoscenza di uno studente europeo che abbia conseguito un
livello A o ``baccalaureate''. Per tutte le altre nozioni matematiche, l'unica
possibilità è quella di utilizzare un elemento generico, associandogli
uno specifico markup di presentazione ed il URI di un documento, la cui forma
non viene specificata, che ne descriva la semantica. Ciò è altamente
insufficiente per la codifica di matematica formale, anche se fornisce un
interessante linguaggio semi-formale utilizzato proficuamente in HELM durante
la fase di rimatematizzazione. La precedente osservazione non si applica alla
parte di MathML per la descrizione della presentazione delle espressioni in
quanto questa è facilmente codificabile attraverso un numero finito di
elementi di markup, come dimostra facilmente il linguaggio di LATEX.
Il secondo motivo per cui
la parte di MathML per la descrizione del contenuto non è adatta alla
codifica della matematica formale, è che ad ogni entità matematica viene
associata la sua semantica standard, che non è definita univocamente in un
contesto formale. Per esempio, all'uguaglianza di MathML corrispondono nei
sistemi formali diverse uguaglianze, come quelle di Leibniz a livello
dei termini e dei tipi o quelle estensionale e intensionale per le funzioni.
Durante la fase di rimatematizzazione, comunque, è naturale identificarle
tutte con l'uguaglianza semi-formale di MathML, a patto che sia possibile
risalire alle loro definizioni formali.
Il secondo standard per la codifica del contenuto matematico nell'ambito del
web-publishing è OpenMath, che si preoccupa di complementare lo standard
MathML definendo una semantica semi-formale per gli elementi contenutistici.
L'uso consigliato di OpenMath in ambito MathML è, infatti, quello di fornire
il formato dei documenti referenziati da MathML per specificare la semantica
per gli elementi contenustici introdotti dagli utenti.
Se si è interessati esclusivamente al contenuto, OpenMath può essere
utilizzato anche separatamente da MathML. Infatti, l'obiettivo dichiarato
di OpenMath è ``la rappresentazione di oggetti matematici con la loro
semantica, permettendone
lo scambio fra programmi, la memorizzazione in database e la pubblicazione sul
WWW''. Concretamente, OpenMath si propone di definire un'architettura per lo
scambio di espressioni matematiche basata su tre componenti: i frasari
(phrasebook), i dizionari di contenuto (content dictionary, CD) e un
formato XML di rappresentazione per questi e per le espressioni matematiche.
I frasari sono interfacce software per la codifica di espressioni
matematiche
dal formato MathML/OpenMath a quello interno delle applicazioni orientate al
contenuto, quali tool per la computer algebra come Mathematica, Maple o Derive.
I content dictionary sono grandi tabelle, ipoteticamente una per
ogni teoria
matematica, che associano ad ogni entità (funzione, relazione, insieme)
una sua descrizione informale e una ``formale'', costituita dalla sua
signature. Per esempio, la descrizione informale della funzione quoziente
(quotient), è ``Integer division operator. That is, for integers a
and b, quotient denotes q such that a=bq+r, with |r| less than |b|
and ar positive.''; la sua signature è il tipo
Z × Z ® Z
dove Z è l'insieme dei numeri interi.
Questo tipo di semantica, che possiamo definire al più semi-formale,
è sufficiente per lo scambio di informazione matematica in
ambiti dove non si è interessati alle prove, ma esclusivamente alle
espressioni; gli obiettivi di HELM sono però molto più ambiziosi e
richiedono una semantica formale sia per i tipi che per i corpi delle
definizioni.
Pertanto, HELM non può beneficiare della semantica di OpenMath. Nonostante
questo, è sicuramente utile, ma non ancora implementato, l'utilizzo di
OpenMath nella rappresentazione semi-formale in MathML content utilizzata
nel progetto HELM.
Nell'ambito dei proof-assistant, esistono due linee di ricerca che hanno
affinità con il progetto HELM. La prima è quella delle interfacce
grafiche. In questo ambito, l'obiettivo è lo sviluppo di sistemi in ambiente
grafico che aiutino l'utente nella visualizzazione e nella ricerca delle
dimostrazioni. Si pone una grossa enfasi sul proof-by-clicking,
ovvero sulla possibilità di applicare tattiche semplicemente selezionando
il termine su cui agire e, per esempio, selezionando il lemma
da applicare.
Fra l'altro, il proof-by-clicking solleva l'utente dall'onere di memorizzare
la sintassi, spesso complicata, del linguaggio delle tattiche dei vari
proof-assistant, creando sistemi utilizzabili per interfacciarsi con
proof-assistant differenti.
Fra questi sistemi ricordiamo Proof General10,
che è sviluppato sotto Emacs e lavora già con diversi proof-assistant fra
cui Coq e Lego, e PCoq11
che è un'interfaccia grafica per Coq
scritta in Java per motivi di portabilità e finalizzata al proof-by-clicking.
Poiché, allo stadio attuale, il progetto HELM non si occupa della ricerca
delle dimostrazioni, il confronto può essere effettuato solo nel campo della
visualizzazione dei termini e delle prove, dove HELM si propone di raggiungere
risultati sicuramente più raffinati.
La seconda linea di ricerca è quella della standardizzazione, a livello
tecnologico o fondazionale, dei proof-assistant. In questo ambito sono stati
proposti due grossi progetti, QED e MathWeb.
QED12, iniziato nel 1994
con la pubblicazione del QED Manifesto [Har94], persegue, come HELM, il
fine della creazione di una grande libreria di documenti matematici
formalizzati. Per realizzarla, viene proposto un approccio fondazionale mirato
alla codifica del contenuto matematico in una logica, detta root logic,
sufficientemente espressiva da rappresentare tutta la conoscenza matematica e,
al tempo stesso, prossima alla logica ``informale'' delle dimostrazioni
cartacee. Il progetto, a cui contribuiscono in maniera determinante gli autori
di Mizar, dopo un primo slancio iniziale13
sembra non aver conseguito grossi successi.
Il motivo principale è da cercarsi nella difficoltà dell'approccio
fondazionale che, sebbene interessante, non permette, almeno per ora, il
recupero dell'informazione già codificata in proof-assistant basati su
logiche non banali. In mancanza di questo, la proposta si riduce al
semplice sviluppo di un nuovo proof-assistant, con in più la complicazione
di trovare un largo accordo, sicuramente utopistico, sulla logica da
utilizzare come root logic. HELM evita accuratamente di commettere lo stesso
errore14,
proponendo
prima di tutto una standardizzazione a livello tecnologico, comunque
propedeutica a qualsiasi studio fondazionale.
Omega è un grosso progetto intrapreso nel 1994 all'Università di Saarland
dal gruppo di ricerca del Prof. Jörg Siekmann per affrontare il delicato tema
dell'integrazione fra proof-assistant e theorem-prover. Successivamente, le
finalità del progetto sono state estese, portando alla nascita del progetto
MathWeb15; oggi,
MathWeb16 è sicuramente il
progetto più simile ad HELM, prevedendo la creazione di una grande libreria
distribuita basata su tecnologia XML. Le differenze fra HELM e MathWeb sono
comunque molteplici; la loro analisi viene rimandata al paragrafo
8.1 quando HELM sarà già stato descritto in dettaglio.
Nonostante questa tesi sia la prima presentazione esaustiva del progetto HELM,
diversi altri lavori sono stati realizzati per descriverne aspetti specifici:
- Studio e progettazione di un modello RDF per biblioteche
matematiche elettroniche [Ric99] è uno studio preliminare, risalente
al 1999, sulla
possibilità di codificare i metadati della libreria di HELM nel formato
standard RDF. Nonostante l'architettura di HELM descritta in questo lavoro
sia stata pesantemente modificata, la parte di lavoro inerente ai metadati
rappresenta un ottimo punto di partenza per le future scelte progettuali.
- Content Centric Logical Environments [APSSa]
è una breve introduzione ai benefici che HELM porterà nell'ambito dei
proof-assistant.
- Towards a Library of Formal Mathematics [APSSc]
presenta l'intero progetto nell'ottica del precedente articolo.
- XML, Stylesheets and the Re-mathematization of Formal Content
[APSSd] affronta il problema della rimatematizzazione del
contenuto formale.
- Formal Mathematics in MathML [APSSb] è una descrizione di HELM
dal punto di vista del web-publishing, incentrato sull'utilizzo di MathML.
1.5 Organizzazione della tesi
Nel capitolo 2 viene introdotto in dettaglio il sistema formale utilizzato
dal proof-assistant Coq. Inoltre, viene data una breve descrizione
delle funzionalità di questo e un semplice esempio d'uso.
Nel capitolo 3 viene descritto il modulo che è stato implementato per
esportare in XML le teorie scritte in Coq. Inoltre, si descrive
l'organizzazione che è stata scelta per i file che compongono la libreria
di HELM.
Nel capitolo 4 viene presentato il modello di distribuzione adottato.
Il capitolo 5 descrive brevemente l'implementazione di un proof-checker per
i file XML che compongono la libreria.
Il capitolo 6 è interamente dedicato alle trasformazioni utilizzate per
associare notazioni alle teorie di HELM.
Il capitolo 7 descrive le interfacce messe a disposizione per la consultazione
della libreria.
Infine, il capitolo 8 riassume lo stato attuale del progetto e lo confronta
dettagliatamente con MathWeb; per concludere, vengono presentati i possibili
sviluppi futuri.
Nel resto di questa tesi vengono assunte la conoscenza da parte del lettore
delle tecnologie XML e XSLT e una buona preparazione nel campo della
logica formale.
- 1
- http://www.w3c.org
- 2
- http://www.mizar.org
- 3
- Il progetto Mizar fu iniziato circa venti
anni fa. La scarsità di documentazione, unita all'utilizzo di codice
proprietario, può far nascere sospetti sulla correttezza dell'intero
sistema.
- 4
- In Coq è naturalmente possibile
definire la funzione appartenenza che, presi in input un insieme I e un
elemento x, ritorna il risultato dell'applicazione di I ad x.
Quindi si può arguire che, se si vuole la notazione x Î I, allora si
deve utilizzare la funzione appartenenza. Anche se in linea di principio
questo è giusto, si avrebbe un consistente aumento della dimensione delle
prove. Inoltre, in presenza di isomorfismi, l'utilizzo di simili artifizi è
pratica comunemente accettata in matematica.
- 5
- http://www.cs.unibo.it/helm
- 6
- I membri attuali sono: Prof. Andrea
Asperti, Dott. Luca Padovani, Sig. Claudio Sacerdoti Coen e Dott. Irene
Schena.
- 7
- L'idea del progetto risale alla fine del 1997.
L'autore contribuisce attivamente al suo sviluppo dall'estate del 1999,
quando è stata definita l'architettura generale ed è iniziata la fase
implementativa.
- 8
- XSLT è lo standard per la descrizione di trasformazioni fra
documenti XML. Un foglio di stile è un documento XSLT che definisce un
insieme di regole di trasformazione.
- 9
- http://www.emis.de/projects/EULER/
- 10
- http://zermelo.dcs.ed.ac.uk/proofgen
- 11
-
- 12
- http://www-unix.mcs.anl.gov/qed
- 13
- Una prima conferenza fu
tenuta nel 1994 ad Argonne, seguita da una seconda a Varsavia nel 1995.
- 14
- Vedi il primo requisito del paragrafo 1.3.1.
- 15
- http://www.mathweb.org
- 16
- Con Omega viene ancora indicato il sotto-progetto mirato
al raggiungimento degli obiettivi originari.
Chapter 2 Il proof-assistant Coq
Coq è un proof-assistant progettato per scrivere specifiche formali e
programmi e per verificare che i programmi soddisfino le loro specifiche.
Viene fornito un linguaggio di specifica, chiamato Gallina, i cui termini
possono rappresentare programmi, loro proprietà o prove di queste.
Grazie all'isomorfismo di Curry-Howard, programmi, proprietà e prove
sono formalizzati nello stesso linguaggio, chiamato Calcolo delle
Costruzioni (Co)Induttive (CIC), che è un'estensione del l-calcolo
caratterizzata da un ricco sistema di tipi funzionali e dalla presenza di tipi
induttivi e coinduttivi primitivi, nello stile di Martin-Löf. L'estrema
espressività di CIC permette di utilizzare Coq anche come un logical
environment per la codifica di teorie matematiche. Per esempio, la
libreria standard di Coq copre la logica del primo ordine, l'aritmetica
sui numeri naturali e quelli interi, una primitiva codifica
della teoria degli insiemi e la teoria assiomatica dei numeri reali, fino
alla definizione e alle prime proprietà delle derivate. In Coq, sono state
sviluppate anche teorie di complessità molto maggiore, come
la Teoria Costruttiva delle Categorie [SH95] o la Teoria degli
Insiemi di Zermelo-Fraenkel [Wer97].
Tutti i judgement logici in Coq sono di tipaggio. Pertanto, il
vero cuore del sistema è il type-checker, che verifica la correttezza
delle prove, ovvero che i programmi soddisfino le rispettive specifiche.
L'architettura di Coq è stata attentamente studiata in modo che la sua
``correttezza'' sia garantita esclusivamente da quella del type-checker.
In altre parole, se CIC è consistente e il type-checker non contiene
bug, allora ogni prova costruita in Coq sarà effettivamente un termine che
dimostra la tesi, ovvero che abita in CIC il termine che la rappresenta.
Come conseguenza, ogni possibile estensione del sistema
che non interessi il type-checker è sicura. In particolare, questo permette
di dare la possibilità all'utente di definire nuove tattiche da aggiungere
al proof-engine.
La seconda componente critica di Coq, oltre al type-checker, è il
program extractor, che permette di sintetizzare programmi funzionali
che obbediscano alle loro specifiche formali, scritte come asserzioni logiche
in CIC. La correttezza del program extractor è necessaria sia per garantire
che il termine funzionale estratto (un termine di Fw) realizzi,
nel senso di Kleene, la prova in CIC, sia per garantire la corrispondenza fra
il codice estratto, scritto nella sintassi concreta di un dialetto di ML,
e il termine di Fw.
La possibilità teorica di descrivere parzialmente1 un sottoinsieme di CIC in CIC stesso, e
in particolare
l'esistenza di un suo type-checker e di un program extractor, permetterebbe
il boot-strapping delle componenti critiche di Coq, ottenendo cosí il
primo proof-assistant certificato. Il progetto, decisamente ambizioso,
è stato portato a termine con successo da Barras e Werner (vedi
[BW97]) per una parte significativa di CIC, ovvero quella puramente
funzionale (il Calcolo delle Costruzioni)2.
Coq e il suo sistema logico hanno rappresentato un difficile, ma stimolante
banco di prova per HELM per diversi motivi.
Innanzi tutto Coq e Lego, basati su dialetti differenti di CIC,
rappresentano i sistemi attualmente più complessi fra quelli basati
sull'isomorfismo di Curry-Howard; a causa dell'architettura assolutamente
monolitica di Coq, che è un tipico prodotto del modello application-centric
che HELM vuole superare, il codice è estremamente complesso; numerose
funzionalità sono state integrate nel sistema in momenti successivi,
portando ad un degrado della pulizia dei singoli moduli, che ora presentano
alti livelli di accoppiamento e bassi livelli di coesione. Per questi motivi,
l'aggiunta al sistema di un modulo per l'esportazione verso XML è stato
un compito non facile e dispendioso in termini di tempo. Un ulteriore motivo
per la scelta di Coq è stato l'elevatissima espressività di CIC, che viene
ripagata con un'alta complessità del sistema logico e conseguente
difficoltà nell'interpretazione dei l-termini. Una tecnica
per rendere comprensibili le prove di Coq, quindi, potrebbe
essere probabilmente applicata con successo anche a sistemi meno complessi.
Nella prossima sezione introdurremo in dettaglio la sintassi e le regole di
riduzione, convertibilità e tipaggio di CIC. Nelle successive presenteremo
alcune caratteristiche di Coq e daremo qualche esempio d'utilizzo del sistema.
2.1 Il Calcolo delle Costruzioni (Co)Induttive
Fra diversi calcoli funzionali tipati, come il l-calcolo, e
le logiche basate su natural deduction esiste un isomorfismo, noto con il
nome di corrispondenza di Curry-Howard. I due sistemi più semplici
messi in relazione sono la logica proposizionale e il l-calcolo
tipato semplice [GLT89]: alle proposizioni corrispondono i tipi del
l-calcolo; agli alberi di prova, i l-termini;
la b-riduzione e l'eliminazione dei tagli completano l'isomorfismo.
Si dice che un termine t abita un tipo T se t ha tipo T.
In altre parole, T è abitato da t se e solamente se t è una
dimostrazione di T. Affinché il sistema sia consistente, è necessario
che un particolare tipo ^ non sia abitato o, equivalentemente, che
esista un tipo disabitato.
Le logiche e conseguentemente i calcoli possono essere classificati in
base alla loro espressività. Questa può essere aumentata in due maniere:
introducendo nuovi oggetti (nuovi tipi) oppure potenziando gli algoritmi
(le astrazioni). Per esempio, il passaggio dalla logica proposizionale al
calcolo dei predicati è ottenuto introducendo nuovi oggetti; quello
dalla logica del primo ordine alle logiche di ordine superiore introducendo
nuove astrazioni. Sfruttando la prima tecnica, diventa possibile definire
direttamente tipi di dati astratti, sia induttivi che coinduttivi,
specificandone i costruttori (le osservazioni nel caso coinduttivo) e i
distruttori, ovvero i principi di (co)ricorsione [Gim94].
La seconda tecnica, invece,
permette la definizione di termini e tipi con gradi sempre maggiori di
dipendenza, che si rispecchiano nel livello di polimorfismo del calcolo:
se nel l-calcolo tipato semplice l'unica astrazione permessa è
quella dei termini sui termini (l-astrazione), nei l-calcoli
del cubo di Barendregt ([Bar92]), in corrispondenza con i sistemi di tipi
puri (PTS), si rendono possibili astrazioni di termini sui tipi e/o di tipi sui
tipi e/o di tipi sui termini (tipi dipendenti).
Un ulteriore elemento che discrimina i sistemi logici è la
predicatività.
Nei sistemi predicativi esiste un ordinamento parziale fra i tipi, che impedisce
le astrazioni su quelli maggiori; in quelli impredicativi non esiste questo
vincolo. La predicatività è un concetto strettamente connesso a quello
di costruttività, in quanto, nei sistemi impredicativi, è possibile
applicare funzioni a tipi non ancora definiti al momento della loro
dichiarazione. In altre parole, la predicatività non permette la definizione
di un oggetto d che riferisca una collezione D della quale d sia
un elemento, evitando circoli viziosi. Nonostante sia possibile
costruire sistemi logici impredicativi consistenti, è molto facile
ottenere sistemi inconsistenti, come mostra Coquand in [Coq86]
applicando il paradosso di Girard a numerosi sistemi impredicativi.
Agli inizi degli anni '70, sono emersi due logical framework, basati sulla
teoria dei tipi, che hanno pesantemente influenzato la definizione di CIC.
Il primo,
la Teoria Intuizionistica dei Tipi di Martin-Löf, cerca una nuova
fondazione della matematica basandosi su principi costruttivi. Il sistema,
predicativo, è caratterizzato da una grande espressività nella definizione
di tipi induttivi.
Il secondo, il l-calcolo polimorfico Fw di Girard, è un
calcolo funzionale impredicativo molto espressivo, nel quale possono essere
rappresentate prove di teoremi scritti in logiche di ordine superiore. I tipi
induttivi possono venire codificati ricorrendo al polimorfismo
(es. i numeri naturali vengono codificati ricorrendo ai numerali di Church).
Nel 1985, combinando le idee di entrambi i sistemi in un'estensione di ordine
superiore del linguaggio del sistema Automath, Coquand presenta la prima
versione del Calcolo delle Costruzioni (CoC).
In questo sistema logico si
possono realizzare potenti assiomatizzazioni, ma i tipi induttivi non possono
essere definiti direttamente, ma solo codificati uniformemente in modo
funzionale, a scapito della semplicità e dell'efficienza implementativa.
Nel 199 Luo [Luo90] ottiene un'estensione consistente del sistema, chiamata
Calcolo delle Costruzioni Esteso, che ammette impredicatività sulle
proposizioni, di tipo Prop, e predicatività per i tipi di dati,
di tipo Typei.
Il formalismo viene nuovamente esteso nel 1989 da T. Coquand e C.
Pauline-Mohring con l'aggiunta di tipi induttivi primitivi, ottenendo il
Calcolo delle Costruzioni Induttive [Coq86].
In seguito all'implementazione di Coq, numerose modifiche sono state proposte
al sistema logico, fra cui le definizioni mutuamente induttive, i tipi
coinduttivi e gli operatori primitivi di analisi per casi e definizione di
funzioni per (co)punto fisso. Poiché le diverse estensioni sono state
date separatamente, non esiste oggi nessun articolo noto all'autore in cui
siano date la sintassi e le regole di tipaggio per l'intero calcolo:
i due lavori più importanti sono la tesi di dottorato di Werner
[Wer94], che descrive la versione originaria di CIC, e
l'articolo di Gimenez [Gim94] in cui vengono introdotte l'analisi per
casi e le definizioni per (co)ricorsione.
Nel prossimo paragrafo e nei successivi,
quindi, verranno descritte la sintassi e le regole di riduzione,
convertibilità e tipaggio di CIC come ricavate dall'autore attingendo a
diverse fonti, compreso il codice di Coq.
In particolare, ringrazio sentitamente Hugo Herbelin che, tramite
comunicazioni private, mi ha enormemente aiutato a ricostruire alcune delle
regole più complesse. Gli eventuali errori presenti sono da attribuirsi
esclusivamente a mie incomprensioni.
2.1.1 La sintassi
In tutto il capitolo, con un piccolo abuso di notazione, le successioni
di qualsiasi genere indiciate da 1 a n potranno essere vuote, salvo
indicazioni contrarie.
Siano
-
V una famiglia numerabile di nomi di variabili, x,y,z,... Î V.
- C una famiglia numerabile di nomi di costanti, c,c1,...,cn Î C.
- I una famiglia numerabile di nomi di tipi (co)induttivi,
i,i1,...,in Î I.
- K una famiglia numerabile di nomi di costruttori di tipi
(co)induttivi,
k,k1,...,kn,k11,...,kn11,...,k1m,...,
knmm Î K.
I termini ben formati, che verranno indicati con t,f,u,T,U,N,M, sono definiti
induttivamente in tabella 2.1.1,
|
|
| t |
::= |
x |
identificatori |
| |
| |
c |
costanti |
| |
| |
i |
tipi (co)induttivi |
| |
| |
k |
costruttori di tipi (co)induttivi |
| |
| |
Set | Prop | Type(j) |
sort |
| |
| |
t t |
applicazione |
| |
| |
l x:t.t |
l-astrazione |
| |
| |
P x:t.t |
prodotto dipendente |
| |
| |
<t>CASESi t OF |
analisi per casi |
| |
|
|
|
| |
|
END |
|
| |
| |
FIXl {x/n1 : t := t ; ... ; x/nm : t := t} |
definizione per punto fisso |
| |
| |
COFIXl {x : t := t ; ... ; x : t := t} |
definizione per co-punto fisso |
|
Table 2.1: Sintassi dei termini di CIC
dove m,n1,...,nm,j e l sono interi positivi, l è
al più uguale al numero di funzioni definite nel proprio (CO)FIX e
x è una sequenza, eventualmente vuota, di identificatori,
la cui lunghezza verrà indicata con
|x|. Con s,s1,...,sn verranno indicate le sort.
Si utilizzerà la notazione T1 ® T2 per P x:T1.T2 quando
x non compare libera in T2. Il tipo induttivo i nel CASES è ridondante,
in quanto tipi induttivi distinti hanno costruttori distinti, e viene indicato
per maggiore chiarezza.
Si noti che, in CIC, non esistono distinzioni fra tipi e termini.
Le parentesi tonde verranno utilizzate per rendere concreta la sintassi
astratta, con l'usuale convenzione per la quale l'applicazione è associativa
a sinistra e la l-astrazione a destra.
Nella l-astrazione e nei tipi dipendenti la x è legata nei corpi,
ovvero dopo il punto. Analogamente, le x sono legate nelle definizioni
per (co)punto fisso nei corpi delle funzioni del proprio blocco,
ovvero dopo i simboli di assegnazione, e dopo le doppie frecce nella
definizione per casi. Le definizioni di variabili libere, di
a-conversione e di sostituzione sono quelle usuali.
Alcune forme di termini hanno usi particolari. Gli arity, definiti
induttivamente nel modo seguente e indicati con A,B,A1,...,An, sono
i tipi dei tipi induttivi. I tipi di costruttori per i, indicati
con C(i),C1(i),...,Cn(i) o semplicemente con C,C1,...,Cn
quando non c'è possibilità di confusione, sono i possibili tipi dei
costruttori del tipo induttivo i.
A ::= s | P x : t.A
| C(i) |
::= |
(i t1 ... th) |
| |
| |
P x : t.C(i) |
| |
| |
T ® C(i) |
-
tutti i tipi mutuamente induttivi con i (compreso i stesso) non
occorrano liberi in t,t1,...,th
- i ¹ x
- Se i dipende da k parametri e il suo arity è
P x1:T1... P xl : Tl.s, allora h = k + l
- i occorra solo strettamente positivamente in T
dove i occorre solo strettamente positivamente in T se
-
tutti i tipi mutuamente induttivi con i non occorrono in T
oppure
- T = P x : T1.T2 e tutti i tipi mutuamente induttivi con i
(compreso i stesso) non occorrono liberi in T1 e i occorre
solo strettamente positivamente in T2 oppure
- T = (i' t1... tn) e i' è un tipo mutuamente induttivo con i
e tutti i tipi mutuamente induttivi con i (compreso i stesso) non
occorrono liberi in t1 ... tn oppure
- T = (i' t1 ... tn) e i', diverso da i, è l'unico tipo
mutuamente induttivo del suo blocco, dipendente da m < n parametri, e
tutti i tipi mutuamente induttivi con i (compreso i stesso) non
occorrono liberi in tm+1,...,tn e occorrono solo
positivamente in modo debole in tutti i tipi dei costruttori di i'
dove i occorre solo positivamente in modo debole in C, tipo di costruttore
di i', se
-
C = (i t1 ... tn) oppure
- C = T ® C' e i appare solo positivamente in modo debole in
C' e i appare solo strettamente positivamente in T dove i' venga
sostituito con una variabile x fresca oppure
- C = P x:T.C' e i occorre solo positivamente in modo debole in C' e
tutti i tipi mutuamente induttivi con i (compreso i stesso) non occorrono
in T dove i' venga sostituito con una variabile x fresca
2.1.2 Le riduzioni e la convertibilità
Prima di dare le regole di riduzione di CIC, è necessario definire i
contesti e gli ambienti.
Contesti e ambienti
Un contesto G è una lista ordinata di dichiarazioni di
variabili (e loro tipi) e prende la forma [(x1 : T1),...,(xn : Tn)]
dove le xi sono tutte distinte. Per indicare che (x:T) è un elemento
di G scriveremo (x:T)ÎG. x Î G significa
$ T.(x:T) Î G. [] denota il contesto vuoto.
Un ambiente E è una lista ordinata di dichiarazioni di (tipi
e corpi di) costanti e di tipi mutuamente (co)induttivi e prende la forma
[w1,...,wn] dove wj ha la forma c : T := t
(dichiarazione di costante c) oppure la forma
| P x1:U1... P xh:Uh. |
| {i1 : A1 := {k11 : C11 ; ... ; k |
|
: C |
|
} ; |
|
| ... ; |
| im : Am := {k1m : C1m ; ... ; k |
|
:
C |
|
} |
|
| }(CO)IND |
Tutti i nomi delle costanti definite in un ambiente debbono essere distinti,
cosí come quelli dei tipi mutuamente (co)induttivi e dei loro costruttori.
Le notazioni per l'appartenenza e l'ambiente vuoto sono le stesse usate
per i contesti. Infine, i Î E e k Î E sono definiti in maniera
ovvia.
Le regole per l'introduzione di definizioni nell'ambiente e nei contesti
verranno date nel paragrafo 2.1.3 essendo mutuamente definite con
le regole di tipaggio di CIC.
Per la sintassi utilizzata in Coq il lettore è rimandato al manuale utente
[BBC+97].
b-riduzione, d-riduzione, i-riduzione e
unfolding (o espansione)
In CIC è necessario definire quattro tipi di riduzioni, chiamate
b-riduzione, i-riduzione, d-riduzione e unfolding
(o espansione).
Le prime due corrispondono all'eliminazione dei tagli per l'implicazione ed
i tipi induttivi. La terza è standard nello studio della semantica dei
linguaggi di programmazione. La quarta si incontra, in forme talvolta meno
ristrette, nei linguaggi di programmazione lazy.
[b-riduzione]
È quella standard: (l x:T.M) N bM{N/x} con la side
condition, usualmente lasciata implicita, che le variabili libere di N non
siano catturate in M{N/x}.
[i-riduzione]
Equivale alla b-riduzione per i tipi (co)induttivi.
Nell'ambiente E contenente la dichiarazione
| P x1:U1... P xh:Uh. |
| {i1 : A1 := {k11 : C11 ; ... ; k |
|
: C |
|
} ; |
|
| ... ; |
| im : Am := {k1m : C1m ; ... ; k |
|
: C |
|
} |
|
| }(CO)IND |
| <T>CASES |
|
(kjl t1 ... th t'1 ... t' |
|
) OF |
|
| k1l |
|
Þ f1 | ... | knl |
|
Þ fn |
|
| END |
|
|
|
fj{t'1/x1 ; ... ; t' |
|
/x |
|
}
|
FIXj {x1/n1 : T1 := f1 ; ... ; xm/nm : Tm := fm}
e COFIXj un'abbreviazione sintattica per
COFIXj {x1 : T1 := f1 ; ... ; xm : Tm := fm}
Si ha
| (FIXj t1 ... t |
|
k) FIX (fj{FIX1/x1 ; ... ;
FIXm/xm} t1... t |
|
k) |
| <T>CASESi (COFIXj t1 ... th) OF |
|
| END |
|
COFIX |
|
|
|
| <T>CASESi (fj{COFIX1/x1 ; ... ; COFIXm/xm} t1 ... th) OF |
|
| END |
|
|
La convertibilità
La convertibilità =bdi fra termini di CIC è semplicemente
definita come la chiusura riflessiva, simmetrica, transitiva e per
contesti4 delle regole di riduzione
b,d,i,FIX e COFIX.
La proprietà di normalizzazione forte5 assicura la decidibilità
della convertibilità. Questa, a sua volta, garantisce la decidibilità del
type-checking, definito nella prossima sezione.
2.1.3 Le regole di tipaggio
Diamo ora le regole di tipaggio per i termini di CIC definendo mutuamente
due judgement.
Il primo, E[G] |- t : T,
asserisce che t, in un ambiente E e in un contesto
G dipendente da E, ha tipo T. Il secondo, WF(E)[G],
asserisce che E è un ambiente valido, ovvero contenente solo definizioni
di costanti e di tipi mutuamente (co)induttivi ben tipati, e che G è
un contesto valido in E, ovvero contenente solo dichiarazioni di variabili
il cui tipo è ben tipato.
Regole del Calcolo delle Costruzioni
WF-Empty
WF([])[[]]
WF-Var
|
E[G] |- T:s
s Î {Prop,Set,Type(i)}
x G
|
|
| WF(E)[G,(x:T)] |
| E[[]] |- T:s E[[]] |- t:T c E |
|
| WF(E;c : T := t)[[]] |
| WF(E)[G] |
|
| E[G] |- Prop:Type(n) |
| WF(E)[G] |
|
| E[G] |- Set:Type(n) |
| WF(E)[G] n < m |
|
| E[G] |- Type(n):Type(m) |
| WF(E)[G] (x:T)Î G |
|
| E[G] |- x:T |
| WF(E)[G] (c:T:=t)Î E |
|
| E[G] |- c:T |
|
E[G] |- T : s1
E[G,(x:T)] |- U : s2
s1 Î {Prop,Set}
s2 Î {Prop,Set}
|
|
|
E[G] |- P x:T.U : s2
|
|
E[G] |- T : Type(n1)
E[G,(x:T)] |- U : Type(n2)
n1 £ n n2 £ n
|
|
|
E[G] |- P x:T.U : Type(n)
|
|
E[G] |- P x:T.U : s
E[G,(x:T)] |- t : U
|
|
|
E[G] |- l x:T.t : P x : T.U
|
|
E[G] |- t:P x:U.T
E[G] |- u : U
|
|
|
E[G] |- (t u) : T{u/x}
|
|
E[G] |- T1 : s
E[G] |- t:T2
E[G] |- T1 = |
|
T2
|
|
|
|
E[G] |- t : T1
|
Regole per i tipi (co)induttivi
Per brevità, in tutte le regole che seguono, con * viene indicata
la seguente dichiarazione di tipi mutuamente (co)induttivi:
| P x1:U1... P xh:Uh. |
| {i1 : A1 := {k11 : C11 ; ... ; k |
|
: C |
|
} ; |
|
| ... ; |
| im : Am := {k1m : C1m ; ... ; k |
|
:
C |
|
} |
|
| }(CO)IND |
|
|
| (E[[]] |- (P x1:U1 ... P xh:Uh.Aj : sj) |
|
|
| (E[[y1:A1* ; ... ; ym:Am*]] |- Clj{y1/i1 ; ... ;ym/im} :
slj) |
|
|
|
| i1,...,im,k11,...,k |
|
distinti |
|
|
|
|
| WF(E,*)[[]] |
|
| dove Aj* = P x1:U1...P xh : Uh.Aj per
j Î {1,...,m} |
| e con il vincolo sintattico che in C11,...,Cnmm i primi h argomenti |
| delle applicazioni la cui testa è uno
dei tipi induttivi i1,...,im siano x1,...,xh |
| WF(E)[G] * Î E |
|
| E[G] |- ij:P x1:U1... P xh:Uh.Aj |
|
se j £ m |
| WF(E)[G] * Î E |
|
| E[G] |- klj:P x1:U1... P xh:Uh.Clj |
|
|
|
|
|
| * Î E
E[G] |- t:(il t1... th t'1... t's) |
| E[G] |- T : A
[(il t1... th):Al{t1/x1 ; ... ; th/xh}|A] |
| (E[G] |- fj : D{Cjl{t1/x1 ; ... ; th/xh},T,(kjl t1 ... th)}) |
|
|
|
|
|
|
E[G] |-
|
æ
ç
ç
ç
ç
ç
ç
è |
|
ö
÷
÷
÷
÷
÷
÷
ø |
: (T t'1... t's t)
|
|
|
|
|
| (E[G,(x1:T1),...,(xm:Tm)] |- fl : Tl) |
|
|
| (GD |
{x1,...,xm,n1,...,nm,x,[],T}) |
|
|
|
|
|
|
E[G] |-
FIXj {x1/n1 : T1 := f1 ; ... ; xm/nm : Tm := fm} : Tj
|
|
| dove fj = l y1:T'1 ... l ynj-1:T'nj-1.
l x:(i t1 ... tn)T |
|
|
|
| (E[G,(x1:T1),...,(xm:Tm)] |- fl : Tl) |
|
|
|
|
|
|
|
E[G] |-
COFIXj {x1 : T1 := f1 ; ... ; xm : Tm := fm} : Tj
|
Restano da definire le condizioni GD,GC e [T:A|B] e
l'operatore D{.,.,.}:
[D{.,.,.}]
Sia T l'insieme dei termini di CIC. Si definisce
D : {C/C è un tipo di
costruttore per i} × T × T ® T
per induzione strutturale sul primo argomento:
| D{(i t1 ... tn),T,t} |
= |
(T t1 ... tn t) |
| D{(x:T)C,T,t} |
= |
P x:t.D{C,T,(c x)} |
In CIC non viene permesso di eliminare un tipo
(co)induttivo di un arity qualsiasi per ottenere un altro tipo. La prima
motivazione è la distinzione fra ciò che è computazionalmente
rilevante in fase di estrazione (ovvero ciò che ha arity Set)
e ciò che non lo è (che ha arity Prop): poiché l'informazione
computazionalmente non rilevante viene eliminata in fase di esportazione,
diventa impossibile eliminare un tipo non informativo per ottenerne uno
informativo, a meno che questo non sia un tipo singoletto (singleton),
ovvero un tipo (co)induttivo con un solo costruttore i cui parametri siano tutti
non informativi. La seconda motivazione è legata all'impredicatività:
come viene mostrato da Coquand in [Coq86], permettendo
l'eliminazione di un tipo impredicativo a favore di uno predicativo, diventa
possibile codificare il paradosso di Burali-Forti nella teoria dei tipi.
In [Wer94] viene spiegato come evitare il paradosso di Coquand
in presenza di tipi induttivi primitivi, limitando l'eliminazione di tipi
all'eliminazione forte, che è l'eliminazione verso Type di
tipi induttivi ``piccoli'' in Set. Diamo, quindi, la definizione di
tipo (co)induttivo piccolo seguita dalla condizione di ammissibilità
dell'eliminazione di un tipo (co)induttivo in favore di un altro:
[Tipo (co)induttivo piccolo]
Un costruttore di un tipo (co)induttivo si dice piccolo se ha un tipo della
forma
P x1:T1 ... P xh:Th.(i t1 ... tn) dove T1,...,Th
hanno tutti tipo Set o Prop.
Un tipo (co)induttivo si dice piccolo quando tutti i suoi costruttori sono
piccoli.
[Condizione di eliminazione di un tipo (co)induttivo]La condizione
[T:A|B] è definita come la più piccola relazione che soddisfa le
seguenti regole:
Prod
| [(i x):A'|B' |
|
| [i:P x : A.A' | P x : A.B'] |
[i:Prop|i ® Prop]
Prop-Singleton
| i è un tipo singoletto |
|
| [i:Prop | i ® Set] |
| s Î {Prop,Set} |
|
| [i: Set | i ® s] |
| i è un tipo (co)induttivo piccolo
s = Type(i) |
|
| [i: Set | i ® s] |
| s Î {Prop,Set,Type(j)} |
|
| [i: Type(l) | i ® s] |
-
se T = P z : M.N e GD{l,M} e GD{l,N} valgono
- se T = l z : M.N e GD{l,M} e GD{l,N}
valgono
- se T = (xj t1... tnj - 1 tnj tnj + 1... tn) se
(GD{l,th})h=1,...,n vale eRS{x1,...,xm,n1,...,nm,x,l,tj} vale dove
j Î {1,...,m}
- se T = (t t1 ... tn) dove t {x1,...,xm} e
(GD{l,th})h=1,...,n vale
- se T è una variabile o una costante o un tipo induttivo o un
costruttore di un tipo induttivo o una sort
- se T = FIXj {y1/n'1 : T1 := f1 ; ... ; yd/n'd : Td := fd}
e (GD{l,Th})h=1,...,d e
(GD{l,fh})h=1,...,d valgono
- se T = COFIXj {y1 : T1 := f1 ; ... ; yd : Td := fd}
e (GD{l,Th})h=1,...,d e
(GD{l,fh})h=1,...,d valgono
- se T=
() e vale una delle seguenti tre condizioni mutuamente
esclusive:
-
i è un tipo induttivo e
t = (z t1 ... tr) dove z Î l È {x} e valgono
GD{l,U}, GD{l,t} e
(GD{l È PR{kh,xh},G'h})h=1,...,d
dove PR{kh,(x1,...,xr)} = {xj / il j-esimo
parametro del costruttore kh è ricorsivo in uno dei tipi induttivi
mutuamente ricorsivi con il suo tipo} e
Gh = l y1:t1 ... l ynh:tnh.G'h dove nh
è il numero dei parametri del costruttore kh.
- i è un tipo coinduttivo
e valgono
GD{l,U}, GD{l,t} e
(GD{l,fh})h=1,...,d
- i è un tipo induttivo, non vale t = (z t1 ... tr)
dove z Î l È {x} e valgono
GD{l,U}, GD{l,t} e
(GD{l,fh})h=1,...,d
dove RS è la condizione definita come segue:
[Condizione RS(Really Smaller)]La condizione RS controlla che
il termine passato come parametro attuale nella posizione occupata dal
parametro formale decrescente riduca, per ogni possibile istanziazione delle
sue variabili libere, esclusivamente a termini più piccoli. La condizione
RS{x1,...,xm,n1,...,nm,x,l,T}
è definita per induzione
sulla struttura di T secondo le regole seguenti, in cui, nelle chiamate
ricorsive, vengono omessi tutti i parametri, tranne gli ultimi due, che sono
gli unici non costanti. La condizione vale6
-
se T = (z t1 ... tn) dove z Î l
- se T = l z : M.N e RS{l,M} e RS{l,N}
valgono
- se T = FIXj {y1/n'1 : T1 := f1 ; ... ; yd/n'd : Td := fd}
e (RS{l,fh})h=1,...,d vale
- se T = COFIXj {y1 : T1 := f1 ; ... ; yd : Td := fd}
e (RS{l,fh})h=1,...,d vale
- se T=
() e vale una delle seguenti tre condizioni mutuamente
esclusive:
-
i è un tipo induttivo e
t = (z t1 ... tr) dove z Î l È {x} e valga
(RS{l È PR{kh,xh},G'h})h=1,...,d
dove PR{kh,(x1,...,xr)} = {xj / il j-esimo
parametro del costruttore kh è ricorsivo in uno dei tipi induttivi
mutuamente ricorsivi con il suo tipo} e
Gh = l y1:t1 ... l ynh:tnh.G'h dove nh
è il numero dei parametri del costruttore kh.
- i è un tipo coinduttivo
e vale (RS{l,fh})h=1,...,d
- i è un tipo induttivo, non vale t = (z t1 ... tr)
dove z Î l È {x} e vale (RS{l,fh})h=1,...,d
[Condizione GC(Guarded by Constructors)]
Scopo di questa condizione è assicurare la normalizzazione forte in
presenza di definizioni di funzione per co-punto fisso (o massimo punto
fisso). In pratica, la condizione richiede che il risultato di ogni
chiamata ricorsiva venga utilizzato come argomento di un costruttore. In
questo modo, il termine di tipo coinduttivo generato dalla chiamata di funzione
``si allunga'' ad ogni iterazione e si possono generare, con politica lazy,
termini aventi un numero infinito di costruttori (osservazioni). Questo non
è in contrasto con la normalizzazione forte, che viene ottenuta combinando
la GC e i vincoli dati sull'unfolding (che è lazy) con l'invariante
che il numero di distruttori (CASES) su tipi coinduttivi in un termine
di CIC è sempre finito. Si noti la dualità con la GD. La condizione
GCh{x1,...,xm,T}, dove h Î {0,1}, x1,...,xm
sono le funzioni definite per co-punto fisso e T è il termine nel quale
le chiamate devono essere guardate, è definita per induzione sulla struttura
di T secondo le regole seguenti, in cui i parametri x1,...,xm vengono
omessi nelle chiamate ricorsive in quanto costanti. La condizione vale
-
se T = (z t1 ... tn) dove z Î {x1,...,xm} e h = 1 e
x1,...,xm non occorrono libere in t1,...,tn
- se T = (k t1 ... tn) dove k è il costruttore di un tipo
coinduttivo che aspetta n parametri e per ogni j Î {1,...,n}
se k è ricorsivo nel j-esimo parametro allora vale
GC1{tj}, altrimenti x1,...,xm non occorrono libere in
tj
- se T = (t t1 ... tn) dove t {x1,...,xm} e t non
è un costruttore di un tipo coinduttivo e x1,...,xm non appaiono
libere in t,t1,...,tn
- se T è una sort o un tipo (co)induttivo o un costruttore di un tipo
(co)induttivo
- se T = l z:M.N e x1,...,xm non occorrono libere in M
e vale GCh{N}
- se T = FIXj {y1/n'1 : T1 := f1 ; ... ; yd/n'd : Td := fd}
e x1,...,xm non occorrono libere in f1,...,fd,T1,...,Td
- se T = COFIXj {y1 : T1 := f1 ; ... ; yd : Td := fd}
e x1,...,xm non occorrono libere in f1,...,fd,T1,...,Td
- se T=
() e x1,...,xm non occorrono libere in U e t
e vale una delle due seguenti condizioni mutuamente esclusive:
-
U = l z:M.(i t1 ... tr) dove i è un tipo coinduttivo
e vale (GCh{fl})l Î {1,...,d}
- U ¹ l z:M.(i t1 ... tr) dove i è un tipo
coinduttivo e x1,...,xm non occorrono libere in f1,...,fd
2.2 Il Calcolo delle Costruzioni (Co)Induttive in Coq
Nella sezione precedente è stato introdotto formalmente CIC in modo che fosse
al tempo stesso facilmente comprensibile e il più vicino possibile
al sistema logico implementato in Coq. In questa sezione verranno descritte
informalmente alcune importanti caratteristiche dell'implementazione di Coq
a cui verrà fatto riferimento nei prossimi capitoli.
2.2.1 Alcune estensioni a CIC
Coq estende la versione di CIC descritta nella sezione precedente in diverse
maniere e con diversi scopi. Vediamo solo le estensioni rilevanti nell'ambito di
questa tesi:
Livelli degli universi impliciti
Chiamiamo livello dell'universo l'indice i in Type(i).
Nonostante nella presentazione data di CIC gli universi
(ovvero le sort Type) siano totalmente
ordinati (dall'indice i), è in verità sufficiente un ordinamento
parziale, generato essenzialmente dalle due side-condition della regola di
tipaggio Prod-T. Per l'utente è estremamente oneroso indicare
esplicitamente i livelli degli universi. Inoltre, dando nuove definizioni
e teoremi, diventa necessario avere un meccanismo di interpolazione dei
livelli. In altre parole, dati due tipi di sort Type(i) e
Type(i+1), è possibile dare una definizione contenente un tipo di
sort Type(j) che, durante il type-checking, deve soddisfare i due
vincoli i < j e j < (i + 1). Se si vuole permetterne la definizione, è
necessario ammettere livelli razionali oppure incrementare tutti i livelli
degli universi maggiori di i + 1. Per questi motivi, in Coq si è scelto
di inferire automaticamente il grafo dell'ordinamento parziale fra i livelli
degli universi. L'utente, quindi, scriverà solamente Type e il
sistema manterrà internamente il grafo dell'ordinamento parziale, verificando
che non si formino cicli, che vengono generati da oggetti non ben tipati.
La soluzione, benché sembri la migliore adottabile, non è esente da
problemi. Il principale è che, fissato un particolare ambiente E, può
succedere che due termini t1 e t2 siano ben tipati se presi separatamente,
ma non lo sia la loro congiunzione a causa di formazione di cicli nel grafo
degli universi. Questo è un esempio minimale dovuto al Prof. Andrea Asperti
e all'autore di questa tesi:
| E |
= |
[ |
(P: Type:= Type ® Type), |
| |
|
|
(Q: Type:= Type ® Type), |
| |
|
|
(p:P := l x:Type.x), |
| |
|
|
(q:Q := l x:Type.x) |
| |
|
] |
|
|
| |
| t1 : Type := (p Q) |
| t2 : Type := (q P) |
In casi non minimali, il vero problema per l'utente diventa capire quali
siano le dichiarazioni che creano ciclicità. Per alleviarlo, una soluzione
possibile è la creazione di un'opportuna interfaccia che permetta di
visualizzare la parte problematica del grafo degli universi, esplicitando
le dipendenze inferite dal sistema. In pratica, comunque, lo strano fenomeno si
presenta raramente7.
Cast
I cast vengono introdotti in CIC per associare esplicitamente un tipo al
termine corrispondente. Per la proprietà dell'esistenza di un tipo
principale per ogni termine di CIC, l'operatore non aggiunge alcuna
informazione ai termini8.
Ciò nonostante, i cast possono essere utili durante la
dimostrazione di un teorema: per esempio, è possibile scrivere tattiche per
inferire alcuni termini; poterne specificare il tipo tramite un cast
aumenta il numero dei casi in cui il termine può essere effettivamente
inferito.
In Coq, il cast viene malamente utilizzato anche per aumentare le prestazioni
del type-checker, inserendo cast nel l-termine per alcuni
termini. In questo modo, quando il tipo del termine verrà successivamente
richiesto, potrà essere recuperato dal cast. L'errore, riconosciuto dal
team di sviluppo di Coq, è l'inserimento di questa informazione all'interno
dei termini utilizzando un operatore che ha già un altro significato: il
risultato è l'indistinguibilità dei due utilizzi del cast. Come conseguenza,
è impossibile risalire al termine originale da quello ``decorato'', il
quale è notevolmente più grande a causa dell'informazione ridondante.
Quest'uso del cast verrà abbandonato nella versione 7 del sistema.
La sintassi concreta utilizzata in Coq per il cast di un termine t al tipo
T è t::T. La regola di tipaggio è quella ovvia:
Cast
Metavariabili
L'isomorfismo di Curry-Howard, che fa corrispondere alle prove completate
i l-termini, può essere esteso per trattare prove non ancora
terminate. L'estensione prevede l'aggiunta ai l-termini delle
metavariabili, che corrispondono alle congetture non ancora provate.
Le metavariabili, che appartengono ad una classe sintattica distinta da
quella delle variabili, sono particolari termini che hanno un tipo, ma
non hanno ancora un corpo. Completare la prova significa abitare il tipo
di ogni metavariabile con un termine ben tipato nell'ambiente e nel contesto
della metavariabile. La sintassi concreta per le metavariabili usata in Coq
è ?i, dove i è un intero e viene data una mappa che ad ogni metavariabile
associa il suo tipo. Utilizzando come sintassi astratta (? : T) per
indicare una metavariabile il cui tipo è T, la regola di tipaggio diventa:
Meta
| E[G] |- T : s |
|
| E[G] |- (?:T):T |
Per esempio, se ?1 è una metavariabile che ha come tipo
P A:Prop.P B:Prop.A ® (A ® B)
® B
allora
l A:Prop. l B:Prop. l H:A. l H0:(A ® B).
(?1 A B H H0)
abita
P A:Prop.P B:Prop.A ® (A ® B)
® B
In Coq, in ogni momento può esistere una sola prova non terminata. È,
però, possibile e auspicabile ammettere l'esistenza contemporanea di più
prove non terminate. Questo corrisponde alla possibilità, negata in Coq,
di introdurre nell'ambiente termini contenenti metavariabili.
Con questa estensione, una prova si dice non terminata se contiene almeno una
metavariabile, oppure se dipende transitivamente da una costante che ne
contiene.
Termini impliciti
I l-termini contengono molta informazione ridondante. Come conseguenza,
diventa possibile scrivere una procedura di type-inference che permette di
omettere alcuni dei tipi contenuti in un termine. Questa è implementata
in Coq, dove i termini lasciati impliciti vengono indicati con un punto
interrogativo o, talvolta, addirittura omessi. Esistono, quindi, due differenti
scelte: aggiungere i termini
impliciti a CIC, come è necessario fare con le metavariabili, oppure evitare
di farlo. In quest'ultimo caso, adottato da Coq, i termini impliciti vengono,
almeno concettualmente, inferiti prima di effettuare il type-checking e il
type-checker non viene modificato. La separazione del motore di type-inference
da quello di type-checking permette di non basare la correttezza dell'intero
sistema sul primo, che diventa un'estensione non critica. Al tempo stesso,
però, non viene aumentata l'efficienza del type-checker, nè diminuita
l'occupazione in spazio dei l-termini inferiti. L'altro approccio
è stato adottato per un diverso sistema logico in [NL98], dove i termini
impliciti vengono aggiunti al sistema logico e il type-checker viene
integrato con la type-inference, ottenendo notevolissimi risultati:
sia la dimensione delle prove che il tempo richiesto per il type-checking
sono in O(n0.62) dove n è il valore ottenuto senza l'introduzione
dei tipi impliciti e le costanti nascoste sono basse.
2.2.2 Particolarità implementative
Come consuetudine in tutti i sistemi basati sull'isomorfismo di Curry-Howard
a partire da Automath, le variabili vengono internamente rappresentate
ricorrendo agli indici di de Brujin. In Coq, inoltre, questi vengono utilizzati
anche per denotare le entità definite in maniera mutuamente induttiva
all'interno del loro blocco. Per esempio, la rappresentazione interna della
definizione
| P A : Prop. { |
| tree : Set := { |
| emptyT : (tree A) ; |
| node:A ® (forest A) |
| } ; |
| forest : Set := { |
| emptyF : (forest A) ; |
| cons:(tree A)® (forest A) ® (forest A) |
| } |
| } |
| P Prop. { |
| tree : Set := { |
| emptyT : (1 3) ; |
| node:3 ® (2 3) |
| } ; |
| forest : Set := { |
| emptyF : (2 3) ; |
| cons:(1 3)® (2 3) ® (2 3) |
| } |
| } |
Un'altra particolarità dell'implementazione di Coq è la rappresentazione
interna dell'operatore CASES, che si presenta, senza alcun ragionevole
motivo, in due forme distinte, una generale e una esclusivamente per
l'eliminazione non dipendente. Nel secondo caso, il tipo dei rami del
CASES, indicato fra parentesi angolose, è privo della
l-astrazione sul termine su cui si effettua l'analisi per casi;
per distinguere le due rappresentazioni, l'unico modo è analizzare la
struttura del tipo del tipo dei rami.
In entrambi i casi, la ridondanza fra il tipo induttivo e i suoi costruttori
viene eliminata a favore del primo, l-astraendo i rami del
CASES sui parametri dei costruttori. Pertanto, il seguente termine
| l n : nat. |
| <l z:nat.nat>CASESnat n OF |
| O Þ O | (S m) Þ m |
| END |
| l nat. |
| <l nat.nat>CASESnat 1 OF |
| O | l nat.1 |
| END |
| l nat. |
| <nat>CASESnat 1 OF |
| O | l nat.1 |
| END |
2.2.3 Il livello degli oggetti, ovvero la manipolazione degli ambienti
Definiamo oggetti tutte le entità che possono essere presenti in
un ambiente. In CIC, esse sono le definizioni di costanti, introdotte
con la regola WF-Const, e le definizioni di tipi mutuamente
(co)induttivi, introdotte con la regola WF-Ind. Coq non solo introduce una
sintassi concreta per queste regole, ma raffina la classe delle costanti in
definizioni e teoremi e introduce due nuovi tipi di oggetti, gli assiomi
e le variabili. Questi ultimi hanno un tipo, ma sono privi di corpo.
Pertanto, non sono soggetti a d-riduzione e hanno, come regola
di introduzione, la seguente:
WF-AxVar
| E[[]] |- T:s c E |
|
| WF(E;c : T)[[]] |
La differenza fra assiomi e variabili verrà spiegata nel paragrafo
2.2.4.
La differenza fra teoremi e definizioni è invece nel loro grado di
opacità:
i teoremi sono, di norma, opachi, ovvero su di essi non viene effettuata
d-espansione, secondo il principio della proof-irrilevance. Le
definizioni, invece, sono, di norma, trasparenti, ovvero soggette a
d-espansione. È possibile, e talvolta utile, modificare l'opacità
di un termine, per esempio per formulare un teorema su una prova o per
costruire tipi di dati astratti, le cui definizioni non sono accessibili se
non nel corpo di determinate funzioni.
2.2.4 Le sezioni e il meccanismo di cottura
Dowek ha introdotto in Coq le sezioni e le variabili, ovvero un
meccanismo per strutturare le teorie matematiche in blocchi al cui
interno vengono utilizzati assiomi che vengono ``scaricati'' all'uscita
dal blocco. Il meccanismo è ben noto ai matematici: per esempio, quando
si formulano teoremi nella teoria dei gruppi, le proprietà che li
caratterizzano vengono date come assiomi; i teoremi vengono poi applicati
a qualsiasi struttura matematica che è provata essere un gruppo, come
l'insieme dei numeri naturali. L'operazione di scaricamento consiste
nell'astrarre, tramite P, tutti i tipi dipendenti da una variabile c
rispetto a c stessa; conseguentemente, tutti i termini dipendenti dalla
variabile scaricata vengono l-astratti sulla prova della variabile
e tutti i termini che da lei dipendevano devono essere applicati alla prova.
Le variabili vengono invece eliminate, in quanto il loro scope è la
sezione che le contiene. Al livello degli oggetti, l'operazione viene
chiamata cottura.
Un semplice esempio, utilizzando la sintassi di Coq, sarà chiarificatore.
Si consideri la seguente teoria:
Section S.
Variable A : Prop.
Variable B : Prop.
Theorem AB_A_B : (A -> B) -> A -> B.
Proof.
Exact [ab:(A ->B)][a:A](ab a).
Qed.
Theorem A_AB_B : A -> (A -> B) -> B.
Proof.
Exact [a:A][ab:(A->B)](AB_A_B ab a).
Qed.
End S.
La sintassi utilizzata da Coq dovrebbe essere autoesplicativa, premesso che
``[x:T]t'' viene usato per ``l x:T.t'', ``(x:T)t'' per
``P x:T.t'' e ``->'' per ``®''.
Dopo la chiusura della sezione (con ``End S''), il suo
contenuto viene cucinato. Il risultato è lo stesso che si sarebbe ottenuto
dando le seguenti definizioni:
Theorem AB_A_B : (A:Prop)(B:Prop)(A -> B) -> A -> B.
Proof.
Exact [A:Prop][B:Prop][ab:(A ->B)][a:A](ab a).
Qed.
Theorem A_AB_B : (A:Prop)(B:Prop)A -> (A -> B) -> B.
Proof.
Exact [A:Prop][B:Prop][a:A][ab:(A->B)](AB_A_B A B ab a).
Qed.
2.2.5 Nomi e section path
Le sezioni contengono una lista ordinata formata da definizioni di oggetti o
da altre sezioni. In questo modo, ad una sezione corrisponde in maniera
naturale un albero, i cui nodi interni sono sezioni e le cui foglie sono
(definizioni di) oggetti. Una teoria di Coq (un file ``.v'') altro non è che
una sezione avente
come nome quello del file. Caricare diverse teorie nell'ambiente significa,
quindi, costruire una foresta. Come conseguenza, risulta immediato associare
ad ogni oggetto un section path, ovvero un identificatore univoco
ottenuto concatenando, con opportuni delimitatori, tutti i nomi delle sezioni
nel cammino radice-foglia e giustapponendoci il nome dell'oggetto.
In verità, però, la chiusura di una sezione e la conseguente cottura di
tutti i suoi oggetti la distruggono, spostando tutte le sue foglie al livello
superiore ed
accorciandone il section path. In questo modo, i section-path
non vengono più utilizzati per identificare gli oggetti, che
restano completamente individuati dal loro nome, e il modello ad albero,
che è estremamente naturale, diventa non più valido. Per esempio,
in quello che segue, la definizione di A data nella sezione
S2 non è valida perché entra in conflitto con quella data
nella sezione S1:
Section S1.
Axiom A : Prop.
End S1.
Section S2.
Axiom A : Prop.
End S2.
Ovviamente, il problema si presenta anche fra definizioni date in teorie
differenti. Poiché è impensabile non creare conflitti fra i nomi
definiti in teorie scritte da autori diversi, gli sviluppatori di Coq hanno
scelto di applicare un meccanismo di shading fra le teorie: la definizione
data nell'ultima teoria caricata è l'unica accessibile.
Anticipiamo subito che, durante la procedura di esportazione da Coq, abbiamo
scelto di identificare tutti gli oggetti per mezzo del loro section path
invece che del loro nome, aderendo al naturale modello ad albero.
2.3 Il sistema Coq
Non intendiamo qui dare la sintassi di Coq o spiegare le tattiche che mette
a disposizione, in quanto non saranno rilevanti nell'ambito di questa tesi.
Rimandiamo, quindi, il lettore al manuale utente [BBC+97] e ai due
tutorial [HKP98] e [Gim98]. Nel prossimo paragrafo,
invece, vedremo
brevemente due caratteristiche interessanti del sistema. In quello successivo
daremo un breve esempio d'utilizzo, il cui scopo è esclusivamente
quello di fornire al lettore una prima impressione sulle potenzialità ed
i limiti di Coq.
2.3.1 Parsing e pretty-printing
In Coq vien fornita all'utente la possibilità di estendere sia le regole
di parsing che quelle di pretty-printing9. Infatti, Coq utilizza una
struttura dati uniforme, chiamata albero di sintassi astratta (AST),
per la rappresentazione interna sia dei termini di CIC, sia dei comandi dati
al sistema. Un tool, chiamato Camlp4 (per Caml Pre-Processor-Pretty-Printer),
permette di definire e modificare a run time i due
insiemi di regole utilizzate per trasformare le sequenze di token della
sintassi concreta da e verso gli AST.
Ogni regola è, a grandi linee, costituita da
due parti: un pattern, che viene confrontato con l'input, e una azione, che
genera l'output corrispondente. La definizione di queste regole permette
di associare notazioni testuali agli oggetti definiti in Coq, eventualmente
rendendo impliciti i parametri che possono essere inferiti dal sistema;
in questo modo, per esempio, è possibile in Coq utilizzare la notazione
A /\ B per (and A B) o quella x = y per
(eq ? x y).
Nonostante questo sistema permetta spesso di rendere i termini più leggibili,
è soggetto a diverse limitazioni:
-
Le regole grammaticali sono fattorizzate sintatticamente: Camlp4 non
tenta di espandere i non terminali per individuare ulteriori fattorizzazioni.
Pertanto, l'utente deve fattorizzare a mano tutte le regole.
- Quando si aggiunge una nuova regola di parsing, non viene controllato
che la grammatica resti LL(1), con conseguenti problemi durante il parsing.
- Le regole vengono rimosse all'uscita delle sezioni, permettendo
esclusivamente la definizione di notazioni locali e costringendo, quindi,
a definire le varie regole al top-level.
- A parte pochi esempi, la notazione testuale è del tutto insufficiente
per la rappresentazione delle espressioni matematiche, normalmente scritte
usando consolidate notazioni bidimensionali a cui è bene non rinunciare,
pena un considerevole aumento della difficoltà di interpretazione dei
termini.
2.3.2 Un esempio d'utilizzo di Coq
In questa sezione, mostriamo un piccolo esempio d'uso di Coq, ovvero
la prova di un semplice teorema, chiamato easy, che afferma che ogni
numero naturale o è 0, oppure è uguale alla somma di 1 e di un altro
naturale. Ad ogni passo descriveremo brevemente lo scopo della tattica
utilizzata e le regole di tipaggio utilizzate da questa per costruire il
l-termine. Enunciamo il teorema:
Coq < Theorem easy: (n:nat)(n = O \/ (EX m : nat | (plus (S O) m) = n)).
1 subgoal
============================
(n:nat)n=O\/(EX m:nat | (plus (S O) m)=n)
Assumiamo n (ovvero utilizzamo Lam):
easy < Intro.
1 subgoal
n : nat
============================
n=O\/(EX m:nat | (plus (S O) m)=n)
Lavoriamo per induzione su n (ovvero utilizziamo Case). La tattica
genera due nuovi goal, uno per il caso base e uno per il passo induttivo,
che andremo a provare separatamente:
easy < Elim n.
2 subgoals
n : nat
============================
O=O\/(EX m:nat | (plus (S O) m)=O)
subgoal 2 is:
(n0:nat)
n0=O\/(EX m:nat | (plus (S O) m)=n0)
->(S n0)=O\/(EX m:nat | (plus (S O) m)=(S n0))
Dimostriamo la disgiunzione provando la parte sinistra (utilizziamo Constr):
easy < Left.
2 subgoals
n : nat
============================
O=O
subgoal 2 is:
(n0:nat)
n0=O\/(EX m:nat | (plus (S O) m)=n0)
->(S n0)=O\/(EX m:nat | (plus (S O) m)=(S n0))
Applichiamo la proprietà riflessiva (utilizziamo Constr in quanto
l'uguaglianza di Leibniz è il tipo induttivo con un unico costruttore
che afferma la riflessività della relazione). Questo termina la prova
del caso base.
easy < Reflexivity.
1 subgoal
n : nat
============================
(n0:nat)
n0=O\/(EX m:nat | (plus (S O) m)=n0)
->(S n0)=O\/(EX m:nat | (plus (S O) m)=(S n0))
Passiamo al passo induttivo. Introduciamo n0 e l'ipotesi induttiva
H (utilizzando Lam due volte):
easy < Intros.
1 subgoal
n : nat
n0 : nat
H : n0=O\/(EX m:nat | (plus (S O) m)=n0)
============================
(S n0)=O\/(EX m:nat | (plus (S O) m)=(S n0))
Dimostriamo la disgunzione provando la parte destra (utilizziamo Constr):
easy < Right.
1 subgoal
n : nat
n0 : nat
H : n0=O\/(EX m:nat | (plus (S O) m)=n0)
============================
(EX m:nat | (plus (S O) m)=(S n0))
Chiediamo, per nostra comodità, di effettuare bdi-riduzione
sul goal (utilizziamo Conv):
easy < Simpl.
1 subgoal
n : nat
n0 : nat
H : n0=O\/(EX m:nat | (plus (S O) m)=n0)
============================
(EX m:nat | (S m)=(S n0))
Il quantificatore esistenziale è definito in Coq nel modo usuale come un
S-tipo, ovvero
come un tipo induttivo con un unico costruttore che prende un valore
e la prova che la proprietà vale per quel valore.
Per completare la prova, pertanto, applichiamo il costruttore al valore
n0 (utilizziamo App e Constr)...
easy < Exists n0.
1 subgoal
n : nat
n0 : nat
H : n0=O\/(EX m:nat | (plus (S O) m)=n0)
============================
(S n0)=(S n0)
...e alla prova che (S n0)=(S n0) (utilizziamo nuovamente App e
Constr):
easy < Reflexivity.
Subtree proved!
La prova è terminata, pertanto possiamo salvarla ...
easy < Qed.
...e chiedere di vedere il l-termine che abbiamo costruito:
Coq < Print easy.
easy =
[n:nat]
(nat_ind [n0:nat]n0=O\/(EX m:nat | (plus (S O) m)=n0)
(or_introl O=O (EX m:nat | (plus (S O) m)=O) (refl_equal nat O))
[n0:nat; _:(n0=O\/(EX m:nat | (plus (S O) m)=n0))]
(or_intror (S n0)=O (EX m:nat | (plus (S O) m)=(S n0))
(ex_intro nat [m:nat](S m)=(S n0) n0 (refl_equal nat (S n0)))) n)
: (n:nat)n=O\/(EX m:nat | (plus (S O) m)=n)
Essendo la dimostrazione molto semplice, è stato necessario utilizzare
solamente tattiche alquanto primitive, di cui è facile comprendere l'operato.
Per casi più complessi, però, le operazioni compiute dalle tattiche sul
l-termine risultano decisamente oscure. Inoltre, si noti che,
nonostante le regole di pretty-printing, il l-termine appare, almeno
a prima vista, poco leggibile e di grandi dimensioni rispetto alla
semplicità della dimostrazione. Fermandosi un attimo ad analizzarlo, però,
magari aiutandosi con le indicazioni date,
sarà semplice individuare tutti i passi logici compiuti: la parte rilevante
della storia dell'intera dimostrazione è memorizzata al suo interno.
I termini associati alle prove non banali, comunque, possono rapidamente
crescere di dimensioni, con conseguente impossibilità di essere interpretati
in questa forma. Per ovviare al problema, almeno parzialmente, Coq mette
a disposizione un tool, chiamato Natural, per generare automaticamente a
partire dal l-termine una sua descrizione in linguaggio naturale.
Nel nostro caso, il risultato è buono, anche se si nota una notevole
artificiosità, specie nel passo induttivo, e resta il problema
dell'insufficienza della notazione testuale:
Coq < Natural easy.
Theorem : easy.
Statement : (n:nat)n=O\/(EX m:nat | (plus (S O) m)=n).
Proof :
Consider an element n of nat.
We will prove n=O\/(EX m:nat | (plus (S O) m)=n) by induction on n.
Case 1. (base):
We have directly O=O.
With this result we have O=O\/(EX m:nat | (plus (S O) m)=O).
Case 2. (inductive):
We know an element n0 of nat such that
n0=O\/(EX m:nat | (plus (S O) m)=n0) (H).
We will prove (S n0)=O\/(EX m:nat | (plus (S O) m)=(S n0)).
We have directly (S n0)=(S n0).
With this result we have
(EX m:nat | (S m)=(S n0)) which is equivalent to
(EX m:nat | (plus (S O) m)=(S n0)).
Q.E.D.
Il risultato ideale, a nostro parere irraggiungibile senza l'intervento umano,
sarebbe:
Theorem : easy.
Statement : (n:nat)n=O\/(EX m:nat | (plus (S O) m)=n).
Proof :
Consider an element n of nat.
We will prove n=O\/(EX m:nat | (plus (S O) m)=n) by induction on n.
Case 1. (base):
We have directly O=O.
Case 2. (inductive, n=(S n0)):
We will prove (EX m:nat | (plus (S O) m)=(S n0)).
Since (plus (S O) m)=(S m) we can choose n0 for m,
yelding the thesis.
Q.E.D.
Per termini più complessi, Natural genera descrizioni eccessivamente
artificiose e talvolta troppo dettagliate, che possono però essere utilizzate
proficuamente come scheletro per una riscrittura in linguaggio naturale della
prova da parte dell'utente, come per l'esempio precedente.
I comandi dati interattivamente al sistema vengono normalmente inseriti
all'interno dei file ``.v'' (per Vernacular, il linguaggio utilizzato per
interagire con Coq). Per motivi di efficienza, è possibile compilare i
file ``.v'' in file ``.vo'', che contengono esclusivamente le definizioni
degli oggetti sotto forma di l-termini e le regole di parsing
e pretty-printing. I file ``.vo'', che sono il vero prodotto del processo
di scrittura delle teorie in Coq, sono in un formato proprietario binario,
soggetto a modifiche ad ogni nuova versione del sistema. Pertanto, per
conseguire gli obiettivi del progetto HELM, è stato necessario sviluppare un
modulo per Coq, descritto nel prossimo capitolo, che permetta di esportare
la rappresentazione interna dei termini e degli oggetti in un formato standard
qual'è XML.
- 1
- Il teorema
di incompletezza di Gödel impedisce la dimostrazione in CIC della sua
stessa strong normalization, in quanto dimostrarlo implicherebbe, come semplice
corollario, la consistenza di CIC. Infatti, in un sistema strong normalizable,
la forma canonica di ogni termine che abita un tipo induttivo ha come testa un
costruttore, di cui il tipo induttivo False che rappresenta ^
è privo; ne consegue che False non è abitato, ovvero che il
sistema è logicamente consistente.
- 2
- In questo caso non
valgono le ipotesi del teorema di incompletezza di Gödel; di conseguenza,
è stato possibile dimostrare anche la strong normalization
- 3
- Per il ragionamento è
sufficiente la forma normale di testa debole.
- 4
- La chiusura per contesti è quella standard, che asserisce le
proprietà di congruenza di =bdi, e non ha relazioni con i
contesti definiti in precedenza.
- 5
- B.Werner in [Wer94]
dimostra la normalizzazione forte di una versione più primitiva di CIC anche
nel caso in cui si consideri la h-conversione. Il risultato è fortemente
basato sugli studi di Geuvers [Geu93]
- 6
- La condizione viene
introdotta in [Gim94] dove è semplicemente il controllo che
T sia un identificatore appartenente a l. La forma presentata qui, che
è inedita a conoscenza dell'autore, è stata ricavata ex-novo (e
successivamente implementata) assieme al Dott. Luca Padovani partendo
dall'osservazione del comportamento di Coq. Non è stata, però, data alcuna
prova di correttezza (ovvero non è stata provata la normalizzazione forte
del sistema quando si utilizzi questa definizione). Pertanto, la definizione
può essere considerata ``sospetta''.
- 7
- Questa affermazione è falsa nello studio delle
teorie che dipendono pesantemente dalla stratificazione degli universi, come
la Teoria delle Categorie, in cui si devono distinguere le categorie grandi
da quelle piccole, e quella degli insiemi, in cui non vanno confusi gli
insiemi grandi e piccoli. In queste teorie, è usuale procedere duplicando
sintatticamente le stesse definizioni contenenti Type al solo fine
di fare inferire al sistema diversi livelli per gli universi: le definizioni
con il livello minore diverranno quelle piccole, le altre le grandi.
- 8
- L'affermazione è falsa se
il livello degli universi viene inferito, come avviene in Coq.
- 9
- Le regole di parsing sono
quelle che permettono di associare alla notazione testuale utilizzata
dall'utente la rappresentazione interna dei l-termini. Le regole di
pretty-printing compiono l'operazione inversa.
Chapter 3 Esportazione in XML da Coq di oggetti CIC
La prima fase dello sviluppo di HELM è stata la progettazione e
l'implementazione di un meccanismo di esportazione delle teorie
scritte in CIC da Coq in XML.
La prima decisione importante è stata
la scelta di quale informazione dovesse essere esportata. In particolare,
è risultato subito evidente che non tutta l'informazione è significativa.
Il principale criterio utilizzato per determinare la rilevanza
dell'informazione è stato porre l'enfasi sul framework logico e non sul
proof-assistant. In particolare, dovrebbe essere esportata tutta e sola
l'informazione necessaria ad un qualsiasi sistema che lavori sulla stessa
versione di CIC. Pertanto, si è scelto di non esportare:
-
Regole di parsing Queste sono chiaramente dipendenti dal
sistema utilizzato. In particolare, dipendono dalla scelta di Coq di
utilizzare una notazione testuale e uno degli obiettivi di HELM è
proprio il superamento delle notazioni testuali per i proof-assistant
in favore del recupero dell'usuale notazione matematica bidimensionale.
- Regole di pretty-printing Queste regole vengono utilizzate
in Coq per determinare la presentazione delle prove. In un sistema aperto
come HELM, la loro resa deve poter essere influenzata da diversi parametri,
fra i quali le scelte notazionali effettuate dall'autore del documento,
le preferenze degli utenti e le capacità del browser che l'utente ha
a disposizione. Per esempio, l'autore del documento potrebbe aver indicato la
rappresentazione dei vettori per colonna, mentre l'utente deve essere libero,
se preferisce, di cambiare la notazione in quella per righe. Inoltre, la
notazione utilizzata in una resa HTML o testuale di un documento deve
necessariamente essere più grezza di quella MathML e sicuramente è
diversa da quella che deve richiedere un utente non vedente.
- Tattiche utilizzate nelle prove e termini impliciti
Innanzi tutto, anche le tattiche
sono tipicamente dipendenti dal proof-assistant utilizzato; inoltre, come
già spiegato a pagina 8, HELM si basa sulla
convinzione che non rappresentino il reale contenuto informativo delle prove
e non siano in corrispondenza con il livello al quale si vorrebbe
leggerle. Pertanto, si è scelto di esportare esclusivamente i
l-termini. Inoltre, adeguandosi alla politica di Coq che inferisce
i termini impliciti senza introdurli a livello CIC (vedi paragrafo
2.2.1), i l-termini esportati apparterranno, almeno in
questa prima implementazione, al sistema logico non esteso con tipi impliciti.
- Informazione ridondante aggiunta per velocizzare l'elaborazione
Coq aggiunge diverse informazioni ai termini di CIC per velocizzare
le elaborazioni. Per esempio, durante il type-checking di una definizione
induttiva, Coq individua quali sono i parametri ricorsivi dei costruttori
e aggiunge l'informazione nelle loro definizioni per utilizzarla poi
durante la verifica della condizione GD per le definizioni per
punto fisso. Se questa informazione fosse esportata, diverrebbe un esempio di
informazione ridondante, sicuramente inutile per il browsing ed eventualmente
inutile per gli altri proof-checker, che dovrebbero comunque verificarne
la veridicità. Abbiamo, quindi, deciso di non esportarla in accordo ad un
principio di minimalismo: nessuna informazione ridondante
deve essere esportata. Quando il principio non viene seguito, ogni volta che
un file XML viene utilizzato si deve controllare la consistenza
dell'informazione ridondante, talvolta allo stesso costo computazionale
del calcolarla1. Purtroppo,
l'indistinguibilità
dei cast ridondanti da quelli necessari (vedi paragrafo 2.2.1) ci ha
obbligato ad esportarli ugualmente.
L'informazione da esportare si riduce quindi ai l-termini, agli
oggetti e alla loro strutturazione. La prossima decisione, quindi,
diventa la scelta di come mappare queste entità su file XML e directory
che li contengano.
Mentre gli oggetti esistono in tutti
i proof-assistant, i termini sono tipici di quelli basati sull'isomorfismo
di Curry-Howard. Inoltre, i termini non compaiono mai isolati, ma solo
all'interno degli oggetti. Per questi motivi, l'unità atomica di informazione
è rappresentata da questi ultimi e abbiamo scelto di associare un file XML
ad ogni oggetto, ad eccezione dei blocchi di tipi (co)induttivi definiti
in maniera mutuamente ricorsiva, ai quali viene assegnato un unico file XML il
cui nome è quello del primo tipo induttivo ivi definito.
Questa scelta è stata motivata anche dalla volontà di
identificare gli oggetti tramite section path (vedi paragrafo
2.2.5) e
non tramite il loro nome. Conseguentemente, si è scelto di esportare tutti i
termini nella loro forma non cucinata, che è quella in cui vengono
definiti dagli autori.
Una volta deciso che ogni oggetto diventa un file XML,
ad ogni sezione, e conseguentemente ad ogni file ``.v'', si può far
corrispondere un directory.
Come è naturale in Coq strutturare ulteriormente i file ``.v'' in directory
(che non hanno un corrispondente nella rappresentazione interna di Coq),
cosí abbiamo deciso di utilizzare altri directory per rappresentare le
sezioni e di far tenere conto ai section path anche delle prime.
Come conseguenza, possiamo organizzare l'intera libreria di HELM in un unico
albero invece di avere una foresta. Si noti che non esiste nessun modo per
discriminare i directory corrispondenti alle sezioni dagli altri: in effetti,
possiamo tranquillamente pensare ai nuovi directory come a sezioni
prive di variabili contenenti esclusivamente altre sezioni. Per esempio,
la definizione della somma fra numeri naturali (plus), che è
una costante definita in Coq nella sezione Peano del file
INIT.v, è stata esportata con il path relativo
alla radice della libreria di HELM ``coq/INIT/Peano/plus.con.xml''.
Si noti che, per mantenere separati gli spazi dei nomi, è stato scelto di
utilizzare suffissi diversi per specificare le classi degli oggetti: ``.con''
per le costanti (definizioni e assiomi), ``.ind'' per i tipi induttivi e
``.var'' per le variabili.
In accordo con il modello di distribuzione, che verrà descritto nel
prossimo capitolo, è stato poi associato ad ogni file XML un nome
logico, sotto forma di URI ottenuto anteponendo al pathname relativo del file
il prefisso ``cic:/'' ed eliminando il suffisso costante
``.xml''. Per esempio, l'URI della somma fra numeri naturali
diventa ``cic:/coq/INIT/Peano/plus.con''
Fino ad ora abbiamo affrontato il problema di preservare l'organizzazione
in sezioni degli oggetti, che è solo una parte dell'informazione di
strutturazione di Coq. Infatti, nella libreria del sistema esiste un
ordinamento totale fra le definizioni degli oggetti all'interno di uno stesso
file ``.v'' e un ordinamento parziale fra questi, dovuto alle dipendenze di
almeno un oggetto di un file da un altro file ``.v''.
Esiste, poi, un secondo ordinamento parziale,
coerente con il primo2, dovuto
alle dipendenze fra gli oggetti CIC3. Confrontando i due ordinamenti, si nota
che il primo può essere considerato semplicemente una linearizzazione
accidentale del secondo, dovuta all'ordine con il quale sono state date
definizioni indipendenti. Un secondo punto di vista, invece, è interpretare
l'ordinamento come quello voluto dall'autore per presentare la teoria
matematica. In effetti, quando in Coq si scrive una teoria (un file ``.v''),
si compiono contemporaneamente due operazioni: la prima è la
scrittura di definizioni e teoremi su queste; la seconda è la scelta
dell'ordine in cui presentarle. Nell'usuale pratica matematica, invece,
le due operazioni sono usualmente distinte e sequenziali: spesso, per
esempio, vengono scritti articoli componendo in maniera differente
definizioni e teoremi sviluppati in precedenza, magari presi da fonti
diverse. In Coq, come spiegheremo fra poco (paragrafo 3.3),
abbiamo voluto distinguere chiaramente l'output delle due fasi, individuando,
oltre ai due livelli dei termini e degli oggetti, un terzo livello, formato
da teorie. Come conseguenza, l'ordine totale di introduzione degli oggetti
viene dimenticato durante l'esportazione da Coq, a favore di quello parziale,
lasciato implicito, delle dipendenze logiche. Purtroppo, però, l'ordine
implicito non è sufficiente per la cottura:
la scelta di esportare gli oggetti nella loro forma non cucinata comporta
la necessità di esportare tutte le informazioni necessarie alla loro
successiva cottura, ovvero la lista, che deve essere ordinata, delle variabili
dalle quali il termine dipende, chiamate ingredienti; l'ordinamento
della lista, che deve essere coerente con quello parziale, è reso necessario
per determinare la sequenza con la quale gli ingredienti devono essere astratti
durante la cottura. Il dover fissare, in maniera largamente arbitraria,
un ordinamento totale per la cottura, suggerisce fortemente che questa
operazione possa essere rimpiazzata con un meccanismo più generale.
In effetti, nella prossima versione di Coq, l'intera gestione delle variabili
e delle sezioni dovrebbe cambiare, eliminando completamente la necessità di
cucinare gli oggetti. Nel frattempo, si è resa necessaria, durante la fase di
esportazione, l'aggiunta ad ogni oggetto cucinabile, ovvero tipi mutuamente
(co)induttivi e costanti, della lista ordinata degli ingredienti da cui dipende.
L'ultima decisione da prendere prima di passare alla definizione del
DTD per i file XML è la scelta di come discriminare oggetti fra loro
sintatticamente indistinguibili, quali teoremi, lemmi, corollari e definizioni.
Queste, infatti, sono tutte costanti cucinabili con un corpo e un tipo e la
classificazione precedente non ha nessun valore a livello logico, ma solo a
quello presentazionale4:
per esempio, la scelta se considerare
una data costante un teorema o un lemma è largamente arbitraria e può
dipendere dal contesto in cui viene inserita; inoltre, è probabilmente del
tutto indipendente dal sistema logico adottato. Pertanto, questa informazione
non verrà inserita nei file XML corrispondenti agli oggetti, ma in quelli,
descritti più avanti nel paragrafo 3.3, che li utilizzano per
descrivere teorie matematiche.
3.1 Una critica all'approccio ``un oggetto, un file''
Proseguendo nell'implementazione di HELM, ci siamo resi conto che
l'uso di un file XML per ogni teorema potrebbe essere proficuamente
abbandonato in favore dell'uso di due file XML, uno per l'enunciato e uno per
la dimostrazione. Esistono almeno due ragioni significative:
-
Spesso, sia durante il proof-checking che durante la sola visualizzazione,
è necessario richiedere solamente il tipo, ovvero l'enunciato, di un teorema,
che è diversi ordini di grandezza più piccolo della prova. Per ottenere
questa informazione, però, è comunque necessario processare l'intero
documento XML, con conseguente grossa inefficienza nel caso della soluzione
ora adottata.
- È possibile e talvolta usuale dare più di una dimostrazione per lo
stesso teorema. Con la soluzione ora adottata, questo significa replicarne
anche l'enunciato, con conseguente spreco di spazio disco.
Pertanto, nella prossima versione si adotterà la soluzione alternativa.
3.2 Il DTD per il livello dei termini e degli oggetti
Il DTD per i file XML degli oggetti CIC, al quale si farà riferimento
in questo paragrafo, si trova in appendice A.
I criteri che hanno guidato la sua definizione sono stati:
-
Separazione del livello dei termini da quello degli oggetti
Gli elementi di markup del livello dei termini devono essere chiaramente
distinti da quelli del livello degli oggetti. Il DTD deve essere il più
possibile modulare per permettere la modifica di un livello con impatti
minimi sull'altro.
- Unicità del namespace I file devono utilizzare un solo
namespace, per due motivi. Il primo è che le dimensioni dei file
XML risultanti sono notevoli, con conseguenti alti tempi di parsing e
trasmissione dei file via rete: l'utilizzo di un solo namespace riduce
notevolmente le dimensioni dei file, permettendo di evitare tutti i
prefissi. Il secondo motivo è che, in futuro, si preferisce avere
un solo namespace per ogni sistema logico, al fine di evitarne la
proliferazione.
- Aderenza alla sintassi astratta di CIC Il DTD deve
seguire il più possibile la sintassi astratta di CIC, evitando
ogni forma di ridondanza, in accordo con il già citato principio di
minimalismo.
- Utilizzo degli URI per riferirsi ad altri oggetti
- Leggibilità Per semplificare lo sviluppo e il
debugging, si deve utilizzare un formato XML che agevoli la comprensione
diretta del contenuto, anche a scapito della concisione. In particolare,
chiunque conosca a fondo CIC dovrebbe essere in grado, con moderato sforzo,
di interpretare un file XML.
Il quinto criterio ha suggerito l'adozione di opportuni tag di
``zucchero sintattico''. Seguendo i primi due criteri, si è scelto
di utilizzare la capitalizzazione dei nomi dei tag XML per distinguere
il livello dei termini da quello degli oggetti e dallo zucchero sintattico.
In particolare, i tag tutti maiuscoli vengono utilizzati per i
termini CIC e quelli tutti minuscoli per lo zucchero sintattico;
i restanti tag, indicati con solo le iniziali maiuscole, sono utilizzati
sia per i tag che specificano il tipo di oggetto, sia per delimitare gli
elementi delle liste (per esempio, i singoli tipi induttivi in un blocco
di tipi definiti mutuamente). Ad eccezione di target, tutti
gli altri elementi di zucchero sintattico sono privi di attributi e
non portano alcuna informazione. Su target vengono posti i binder,
ovvero i nomi delle variabili legate nelle
l-astrazioni e nei prodotti dipendenti. Se si volesse eliminare
lo zucchero, il binder dovrebbe essere rispostato sull'elemento genitore:
la scelta di metterlo su target è stata conforme al quinto
criterio; la variabile, infatti, è legata esclusivamente nell'albero
radicato in target e posizionarla su questo elemento aiuta notevolmente
il colpo d'occhio.
Passiamo alle descrizioni degli ulteriori vincoli sintattici non esprimibili
con il DTD e degli attributi che possono risultare non chiari:
-
ID Gli elementi XML corrispondenti ai termini e agli
oggetti CIC hanno tutti l'identificatore univoco chiamato id.
La motivazione della sua introduzione, legata esclusivamente alla
presentazione, viene rimandata al paragrafo 6.1.
- name Gli elementi XML corrispondenti agli oggetti hanno tutti
l'attributo name che contiene il nome dell'oggetto che deve essere
uguale a quello ottenuto dall'URI del file privato del suffisso. L'attributo,
chiaramente ridondante, potrebbe essere eliminato nella prossima versione.
- params È l'attributo degli elementi XML corrispondenti agli
oggetti CIC cucinabili che specifica la lista ordinata degli ingredienti.
Poiché questi sono variabili contenute nel percorso foglia-radice
nell'albero delle sezioni/directory, i loro URI relativi a quella
dell'oggetto hanno sempre una forma esclusivamente ascendente. Questo rende
possibile utilizzare una codifica molto compatta, la cui sintassi è
| n1: v11 ... v |
|
n2: v21 ... v |
|
... nh: vh1 ... v |
|
- paramMode È un attributo delle definizioni e dovrebbe sempre
essere omesso. Viene spiegato nel paragrafo 3.4.
- binder L'attributo binder associato ad un indice di
de Brujin il cui valore è value deve sempre essere uguale
al valore dell'omonimo attributo dell'elemento target del binder
a cui si riferisce l'indice.
- relUri È l'attributo di un riferimento a variabile VAR
che ne indica l'URI relativo codificato come ``n,v'' dove v è il nome
della variabile e n un intero non negativo con la stessa semantica di quelli
dell'attributo params.
- noType e noConstr Poiché ad un blocco di tipi (co)induttivi
definiti in maniera mutuamente ricorsiva viene assegnato un solo file, per
identificarne un tipo è necessario l'URI del file e l'indice, che viene
fatto partire da zero, del tipo all'interno del blocco, memorizzato
nell'attributo noType; per identificare un costruttore, alla
precedente informazione è necessario aggiungere l'indice del costruttore,
che viene fatto partire da uno5.
In appendice C è riportato, a titolo di esempio
chiarificatore, il file XML corrispondente al teorema dimostrato nel paragrafo
2.3.2 e il cui l-termine è stato dato a pagina
54.
3.3 Il livello delle teorie
Come preannunciato, in HELM, oltre ai livelli dei termini e degli oggetti,
che dipendono dal sistema logico, ne esiste un altro, quello
delle teorie matematiche, che è indipendente dal logical framework.
Nella nostra visione, una teoria è un documento matematico strutturato
contenente oggetti scelti in modo quasi completamente libero da sezioni
differenti.
Scrivere una nuova teoria, dopo una fase preliminare nella quale vengono
sviluppati nuovi oggetti, dovrebbe consistere nell'``assemblaggio'' nel
documento matematico di questi oggetti e di altri definiti in precedenza.
È durante la creazione della teoria che la semantica degli oggetti viene
ulteriormente arricchita e, per esempio, i teoremi vengono classificati come
lemmi, fatti, corollari, etc. Ovviamente, ogni teoria, che viene codificata
in un unico file XML, non include direttamente le definizioni degli oggetti,
ma solamente riferimenti a questi. Come conseguenza, le teorie di HELM sono
essenzialmente differenti dai file ``.v'' che nella terminologia di Coq vengono
chiamati teorie. Per esempio,
è possibile scrivere più teorie HELM che presentano in maniera differente
gli stessi risultati, per esempio omettendo certe dimostrazioni o riportando
anche i lemmi tratti da altre teorie.
In Coq, questo non è possibile in quanto i teoremi comuni
andrebbero replicati in entrambi i file ``.v'' e, a parte lo spreco di spazio
disco, per il sistema risulterebbero completamente scorrelati.
Nelle teorie è utile prevedere un elemento di strutturazione, che chiameremo
sezione, che delimiti lo scope delle dichiarazioni di variabili. Nel caso di
CIC, alle sezioni della teoria corrisponderanno esplicitamente le sezioni
(directory) in cui sono strutturati gli oggetti:
per includere nella teoria un riferimento a una definizione D che dipende da
una variabile V entrambe appartenenti ad una sezione R, è necessario
aprire nel file della teoria la sezione che si riferisce a R tramite URI
e mettere i due riferimenti dentro la sezione. Se non si prevedesse un
meccanismo del genere, la teoria potrebbe diventare ingannevole,
inducendo il lettore a credere, per esempio, che un teorema utilizzi un certo
assioma, che è una variabile della sezione, quando in effetti ne utilizza
un altro. Per questo motivo, nei documenti matematici si presta sempre
attenzione allo scope delle ipotesi formulate.
Questa parte del progetto HELM è attualmente allo stadio embrionale, anche se
esistono già come prototipi per le teorie un DTD, un proof-checker, un
browser, dei meccanismi di applicazione delle notazioni e uno script in grado
di generare una teoria a partire da un file ``.v''.
Poiché si prevedono numerosi raffinamenti nel breve periodo, in questa tesi
non verrà descritto in dettaglio lo stato attuale delle teorie;
ciò nonostante, si farà talvolta loro riferimento nel seguito.
Pertanto, un piccolo esempio può servire ora a chiarirne il concetto:
<?xml version="1.0" encoding="ISO-8859-1"?>
<!DOCTYPE Theory SYSTEM "http://localhost:8081/getdtd?url=maththeory.dtd">
<Theory uri="cic:/coq/INIT/Logic">
<!-- Require Export Datatypes -->
<DEFINITION uri="True.ind"/>
<DEFINITION uri="False.ind"/>
<DEFINITION uri="not.con"/>
<SECTION uri="Conjunction">
<DEFINITION uri="and.ind"/>
<VARIABLE uri="A.var"/>
<VARIABLE uri="B.var"/>
<THEOREM id="id1" uri="proj1.con"/>
<THEOREM id="id2" uri="proj2.con"/>
</SECTION>
<SECTION uri="Disjunction">
<DEFINITION uri="or.ind"/>
</SECTION>
</Theory>
L'esempio è un frammento di una teoria ottenuta a partire dal file ``.v''
della libreria standard di Coq in cui vengono definiti gli usuali operatori
della logica proposizionale.
Tutti gli URI, a parte quello di Theory, sono relativi. Quindi,
per esempio, l'URI assoluto di id1 è
``cic:/coq/INIT/Logic/Conjunction/id1''.
Nell'esempio viene anche mostrato l'uso delle sezioni per limitare lo scope
delle variabili: quello di A e B è la sezione
Conjunction.
È importante notare che, al livello delle teorie, le sezioni non vengono
utilizzate per strutturare il documento in, per esempio, capitoli, paragrafi,
etc.: già numerosi linguaggi di markup, istanze di XML, sono stati
sviluppati per questo. In accordo allo spirito di XML, il nostro markup potrà
essere liberamente e modularmente intervallato ad altri tipi di markup XML,
fra cui XHTML6. Dunque, il nostro
linguaggio può aspirare ad avere per le teorie matematiche lo stesso ruolo
di MathML per le espressioni matematiche e
SVG7 per la grafica vettoriale. Infine,
è bene rilevare che il valore
aggiunto dall'utilizzo del livello delle teorie rispetto alla semplice
replicazione della definizione degli oggetti è non solo quello di arricchirne
la semantica, ma anche quello di aggiungere vincoli di natura presentazionale,
quali quello sullo scope delle variabili.
3.4 L'implementazione del modulo di esportazione
Una volta individuata tutta l'informazione da esportare, prima di passare
all'implementazione bisogna deciderne la fonte. Le due uniche possibilità
erano caricare i file ``.vo'' e interpretarne il contenuto, oppure estendere il
sistema con un modulo in grado di accedere direttamente alle strutture dati
interne. La prima soluzione è sembrata impraticabile, sia perché il
formato del file, che cambia ad ogni versione di Coq, non è documentato,
sia perché, cosí facendo, non avremmo potuto utilizzare nessuna delle
funzioni messe a disposizione dal sistema per astrarne la rappresentazione
interna: infatti il Calcolo delle Costruzioni (Co)Induttive
è codificato in Coq come un'istanza di un ulteriore metalinguaggio, pensato
originariamente per permettere l'estensione del sistema ad altri logical
framework. Pertanto, abbiamo optato per la seconda soluzione, utilizzando
i meccanismi standard messi a
disposizione in Coq per estendere il sistema con opportuni moduli, scritti
in OCaml8,
che hanno accesso alle strutture dati
interne. In particolare, si è scelto di scrivere un modulo per aggiungere al
vernacolo9 i
seguenti comandi:
-
Print XML id.
-
Visualizza in XML la forma disponibile più cucinata dell'oggetto il cui
nome è id.
- Print XML File "pathname" id.
-
Crea il file XML il cui pathname è pathname per la forma
disponibile più cucinata dell'oggetto il cui nome è id.
- Show XML Proof.
-
Visualizza in XML la prova parziale del teorema in corso di dimostrazione.
- Show XML File "pathname" Proof.
-
Crea il file XML il cui pathname è pathname per la prova parziale
del teorema in corso di dimostrazione.
- Print XML Dir id.
-
Visualizza ricorsivamente in XML la sezione già chiusa il cui nome
è id. Gli oggetti vengono stampati nella loro forma non cucinata,
correlata con le informazioni per la cottura.
- Print XML Dir Disk ``dirname'' id.
-
Crea ricorsivamente i directory e i file XML per le sezioni e gli oggetti
contenuti nella sezione già chiusa il cui nome è id.
Gli oggetti vengono stampati nella loro forma non cucinata, correlata con le
informazioni per la cottura; il nome del directory che viene creato come
radice è dirname.
Nonostante il compito sembrasse semplice, si sono presentati numerosissimi
problemi, almeno uno dei quali non risolvibile senza modificare il sistema.
Descriviamo brevemente solamente i due problemi che non sono stati risolti
all'interno del sistema.
Il primo è dovuto al fatto che Coq, dopo il caricamento, non mantiene
internamente alcuna informazione sul pathname dei file ``.v''. Pertanto, tutti
gli URI generabili sono solamente suffissi degli URI completi: per esempio, in
mancanza dell'informazione sul fatto che il file ``Peano.v'' risieda
nel directory ``INIT'' della libreria standard di Coq, l'unico URI
associabile alla somma fra numeri naturali diventa
``cic:/Peano/plus.con'', mentre l'URI esatto è
``cic:/coq/INIT/Peano/plus.con''. Il secondo problema è dovuto
al fatto che Coq mantenga per i diversi tipi di oggetti differenti
informazioni per la cottura.
Senza scendere nei dettagli, per le costanti l'informazione
accessibile è insufficiente, costringendo a rifare il calcolo per
determinarla. Questo può essere ovviamente effettuato all'interno di Coq,
senza però trarne alcun beneficio; al contrario, in questo modo si
è costretti a
lavorare con il metalinguaggio. Il primo problema, invece, non può proprio
essere risolto senza modificare Coq.
A causa dei precedenti problemi, le procedure di esportazione implementate
non generano file XML
corretti, in quanto tutti gli URI sono errati e la lista degli ingredienti
di alcune costanti, per le quali l'attributo XML paramMode viene
settato al valore POSSIBLE, possono contenere variabili spurie,
ovvero variabili dalle quali l'oggetto non dipende veramente. Per riparare
i file esportati, sono stati sviluppati due strumenti. Il primo è uno
script Perl10 che analizza l'intero albero
dei file esportati da Coq e aggiunge a tutti gli URI il prefisso mancante.
La possibilità di associare in maniera univoca tale prefisso all'URI è
garantita dalla politica di naming di Coq.
Il secondo strumento, scritto in OCaml, implementa una visita di tutti gli
oggetti per i quali paramMode = POSSIBLE e di tutti quelli da loro
riferiti per determinare quali variabili debbano essere eliminate
dall'attributo param in quanto non occorrono nei l-termini
da cui l'oggetto dipende.
Sia il modulo di esportazione che i due strumenti aggiuntivi non vengono
qui descritti in dettaglio in quanto, entro la fine del 2000, è previsto
un periodo in cui l'autore di questa tesi si recherà presso l'INRIA per
riscrivere il modulo di esportazione per la nuova versione di Coq, attualmente
sotto sviluppo e in fase di implementazione. La stretta collaborazione
è mirata principalmente alla risoluzione dei problemi che hanno portato allo
sviluppo dei moduli aggiuntivi; inoltre, verranno propagati ad HELM i
cambiamenti apportati a Coq, quali la riorganizzazione del meccanismo di
gestione delle sezioni e delle variabili.
3.4.1 Risultati ottenuti
Sono state esportate con successo l'intera libreria standard di Coq e una
teoria di dimensioni medio-grandi. Per quanto riguarda la libreria standard,
l'esportazione ha richiesto circa 4 minuti, mentre le due fasi di riparazione
hanno richiesto rispettivamente 3 e 25 minuti. I file creati sono stati
2664, i directory 249; l'occupazione complessiva su disco è di 79 Mbyte,
che scendono a soli 4 Mbyte se compressi con il programma gzip, basato
sull'algoritmo Lempel-Ziv. Sulle dimensioni
incidono notevolmente gli spazi utilizzati per indentare i tag XML: nei
teoremi più grandi si trovano fino a 130 livelli di indentazione.
- 1
- Effettivamente, in alcuni casi abbiamo esportato
informazione ridondante quando questa era necessaria per la presentazione
e computazionalmente molto costosa da ricavare.
- 2
- Con coerenza si intende che
l'ordinamento parziale è un sottoinsieme di quello totale.
- 3
- Il grafo
delle dipendenze è aciclico: questa proprietà è garantita dalla coerenza
del sistema logico, ovvero, in ultima analisi, dalle regole di tipaggio e
validità degli ambienti.
- 4
- L'indistinguibilità delle definizioni dai
teoremi può, a prima vista, stupire. Non si dimentichi, però, che la
principale caratteristica del Calcolo delle Costruzioni, di cui CIC è
un'estensione, è proprio l'indistinguibilità dei tipi dai termini, con la
conseguente possibilità di ragionare sulle prove, ovvero di scrivere teoremi
che abbiano come oggetto dimostrazioni.
- 5
- La differenza fra la base dei due
indici ha ragioni storiche: nella letteratura su Coq, infatti, sono usuali
formalizzazioni di CIC in cui le definizioni dei tipi (co)induttivi non sono
presenti nell'ambiente, ma vengono replicate nel l-termine ad ogni
loro occorrenza, similmente a quanto avviene per i blocchi di funzioni
definite mutuamente per (co)punto-fisso. In queste presentazioni, la diversa
base dei due indici aiuta a contenere le dimensioni delle espressioni poste
come pedici nelle formule.
- 6
- http://www.w3.org/TR/xhtml1
- 7
- http://www.w3.org/TR/SVG
- 8
- OCaml è un linguaggio di programmazione fortemente tipato,
funzionale, ad oggetti e con la possibilità di utilizzare anche costrutti
imperativi; come Coq, è sviluppato all'INRIA. Coq e tutti i moduli che lo
estendono sono scritti interamente in OCaml.
- 9
- Il vernacolo è il linguaggio dei comandi di Coq.
- 10
- Perl è sicuramente il linguaggio più adatto
per effettuare elaborazioni di file fortemente basate sulla ricerca o sulla
sostituzione di parti di testo con altre. In particolare, si noti che
l'intero script tratta i file XML come semplici file di testo, sostituendo
gli URI incompleti con quelli completi ricavati dall'analisi dell'albero
del directory e producendo file XML validi (supposta la validità di quelli
dati in input).
Chapter 4 Il modello di distribuzione
Uno dei requisiti di HELM (vedi 1.3.1) è quello di
permettere a chiunque abbia uno spazio HTTP o FTP di pubblicare un
proprio documento matematico, senza aver bisogno di far girare alcun
programma sul lato server. Come conseguenza, per scaricare un documento
è necessario conoscerne l'URL. L'utilizzo di URL per identificare i
documenti che compongono la libreria di HELM non è, però, una buona
scelta per diverse ragioni:
-
Scarsa efficienza e fault-tolerance Un URL identifica
il server su cui risiede l'unica copia del documento. Pertanto,
tralasciando la possibile esistenza di proxy o cache, il server
rappresenta un collo di bottiglia per le prestazioni e un
single point of failure1.
- Mancata rilocabilità dei documenti Modificare la
posizione fisica di un documento, per esempio spostandolo su un
altro server, cambia il suo URL, con conseguenti problemi di
collegamenti interrotti (broken link). Questi sono inaccettabili,
in particolar modo in una libreria di documenti matematici formali,
in quanto di un oggetto si può fare il type-checking esclusivamente
se sono accessibili tutti i documenti dai quali esso dipende.
- Impossibilità per l'editore di un documento di cancellarlo
È un problema strettamente legato al precedente, ma distinto.
Può accadere che qualcuno pubblichi un documento che, a distanza di
tempo, non ritenga più utile. Pertanto, deve essere libero di cancellarlo
(qualsiasi affermazione contraria sarebbe, a dir poco, utopistica).
Questa operazione, però, invalida tutti i documenti che da quello
dipendono.
Un primo passo verso la soluzione dei precedenti problemi è
l'identificazione dei documenti tramite nomi logici, che possono
assumere la forma di URI, la cui sintassi viene descritta nell'RFC 2396.
In particolare, il formato degli URI per gli oggetti CIC della libreria
di HELM può essere molto semplice. Attualmente, come già spiegato
nel paragrafo 3, associamo ad ogni
documento un URI ottenuto anteponendo ``cic:/''
al suo path relativo al directory di base della libreria, eliminando
poi il suffisso costante ``.xml''.
L'utilizzo di nomi logici fa nascere
l'esigenza di una politica di naming per impedire che a documenti diversi
venga assegnato lo stesso nome. Il problema, che non si pone nel caso
degli URL, non è ancora stato affrontato e lo sarà solamente quando
il progetto uscirà dalla fase sperimentale. Comunque, la soluzione più
semplice è la creazione di una naming authority, che potrà essere
centralizzata o distribuita. Altre soluzioni verranno comunque prese in
considerazione.
Una volta introdotto l'uso di nomi logici, diventa possibile permettere
l'esistenza di più istanze identiche di uno stesso documento,
identificate dallo stesso URI. Opportuni strumenti, descritti nel
prossimo paragrafo, si occuperanno della risoluzione dei nomi logici negli
opportuni nomi fisici.
Se le occorrenze multiple dei documenti aprono la strada alla risoluzione
dei problemi di bilanciamento del carico, fault-tolerance e rilocabilità
dei documenti, generalmente introducono problemi di consistenza fra le
differenti copie. Questi problemi sono assenti nell'ambito di HELM per
via di una caratteristica peculiare dei documenti che descrivono oggetti
matematici, che è la loro immutabilità: la correttezza di un oggetto A
che dipende da un documento B può essere garantita solamente se B non
cambia. L'immutabilità dei documenti garantisce automaticamente la
consistenza fra le diverse copie. Inoltre, essa non impedisce l'esistenza
di diverse versioni del documento, ma semplicemente la mutabilità di
ognuna di queste. Per esempio, è ragionevole
pensare di poter rilasciare una nuova versione del documento quando
viene trovata la dimostrazione di una congettura.
Il terzo problema citato all'inizio del capitolo, legato all'impossibilità
di cancellare i documenti, scompare in presenza di occorrenze multiple
identificate dallo stesso nome logico. Infatti, anche per motivi
prestazionali, diventa usuale effettuare copie locali dei documenti
acceduti frequentemente o di quelli da cui dipendono le proprie teorie;
inoltre, una volta effettuata la copia, questa può essere messa
a disposizione di tutti.
In questo modo, entra in azione un meccanismo di selezione naturale, per il
quale i documenti più interessanti si diffondono rapidamente, mentre gli
altri scompaiono quando ne viene cancellata anche l'ultima copia.
Forti sono le analogie fra i documenti della libreria di HELM ed
i package utilizzati per l'installazione di programmi, per esempio
nelle diverse distribuzioni del sistema operativo Linux.
Infatti, affinché un programma possa venire mandato in esecuzione,
le librerie installate nel sistema devono fornire le funzionalità attese,
ovvero o devono non essere cambiate rispetto alla versione sulla quale
è stato compilato il programma, oppure devono essere di una versione più
recente e compatibile all'indietro. In sostanza, anche i package
devono essere immutabili, ma deve essere possibile rilasciare una nuova
versione del package quando il programma viene aggiornato. Inoltre,
anche i package sono usualmente replicati su diverse macchine e vengono
talvolta identificati da nomi logici. Pertanto, è naturale scegliere
un modello di distribuzione simile.
In particolare, abbiamo adottato il modello utilizzato dalla distribuzione
Debian2, che si basa sul sistema Advanced
Package Tool (APT),
uno strumento che, in HELM, viene chiamato getter. Al
getter APT viene fornita dall'utente una lista di server
(HTTP, FTP, NFS, etc.) ordinata secondo un qualche criterio che, usualmente,
è il tempo di accesso dovuto al carico del server e alla sua lontananza
fisica. Su richiesta, APT contatta tutti i server della lista, che forniscono
l'elenco dei package a loro disposizione (con le relative versioni). Con queste
informazioni, APT costruisce un cache in cui associa ad ogni nome logico
l'URL dell'istanza del pacchetto sul primo server della lista che lo fornisce.
Successivamente, quando l'utente richiede il pacchetto, APT accede al proprio
cache, individua l'URL, contatta il server corrispondente e scarica sul
file-system la copia fornita.
Basandosi sul modello di APT, nel prossimo paragrafo descriveremo i requisiti
e due diverse implementazioni di un getter per HELM.
4.1 Il getter
Queste sono le funzionalità di base che devono fornire i getter per HELM:
-
Un modo per l'utente di specificare un insieme di server da contattare
e un insieme di regole da utilizzare per generare un ordinamento parziale,
dipendente dal singolo documento, fra i server che lo forniscono.
- Una funzione di update, da eseguirsi in modo batch, per
costruire un cache che associ ad ogni URI un URL, basandosi sui due insiemi
dati in precedenza.
- Una funzione, chiamata get, che, dato un URI, restituisca il
documento associato.
Altre funzionalità che i getter possono fornire sono:
-
Metodi intelligenti di scaricamento basati sulla località dei
riferimenti. Per esempio, il getter potrebbe autonomamente effettuare il
download di tutti i documenti riferiti dal documento scaricato e
successivamente richiesti con alta probabilità.
- Scaricamento di file compressi.
Se il server che fornisce il documento
lo fornisce, staticamente o su richiesta, anche o solamente in modalità
compressa, il getter diventa responsabile non solo dello scaricamento, ma
anche della successiva decompressione.
- Scaricamento di più file contemporaneamente.
Al getter potrebbe
venire richiesto di effettuare il download di un insieme di file.
La funzionalità diventa particolarmente interessante se combinata con le
precedenti.
- Ricostruzione ``al volo'' di documenti.
Il getter potrebbe saper gestire
URI che identificano documenti che debbono essere creati assemblando
opportunamente informazioni ricavate da fonti distinte, per esempio
effettuando la fusione di documenti residenti su diversi server o ottenuti
contattando database remoti.
L'interazione fra il getter e i suoi client, infine, deve poter avvenire
secondo le modalità a loro disposizione. Questo determina l'esigenza di
avere più di una implementazione. Attualmente, infatti, sono stati
sviluppati due diversi prototipi: il primo è un modulo OCaml che, una
volta effettuato il download dei documenti, li salva su disco; il secondo
si comporta come un server HTTP che restituisce i documenti scaricati
come risultato delle richieste HTTP.
4.1.1 Il getter con interfaccia OCaml
Il primo prototipo sviluppato è un modulo OCaml, che è stato
successivamente utilizzato nello sviluppo del proof-checker (vedi capitolo
5).
Le sole funzionalità implementate sono state quelle di base.
In particolare, serve un getter in grado di utilizzare un cache permanente
su disco. In altre parole, ogni volta che il getter scarica un file, lo
memorizza su disco e utilizza questa copia per le successive richieste.
Progettazione
La progettazione è stata estremamente semplice in quanto le richieste erano
ben dettagliate. In particolare si è deciso che:
-
Ogni server, di tipo HTTP o FTP, mantiene i file della libreria di HELM
strutturati secondo la gerarchia descritta nel precedente capitolo.
Come conseguenza, alla radice della gerarchia resta associato un URL.
Inoltre, un server può mantenere più gerarchie distinte identificandole
con URL distinti.
- Ogni server fornisce, nel directory base della gerarchia, un file
contenente la lista degli URI di tutti gli oggetti esportati. Il formato
del file può essere ragionevolmente sia testuale (un URI per linea),
sia XML. Poiché la lista non deve subire elaborazioni particolari, a causa
della banalità del parsing del formato testuale e per
motivi di efficienza (le liste conterranno mediamente diverse migliaia di
elementi), si è scelto di utilizzare il formato testuale, che richiede
meno spazio su disco e tempi di parsing molto minori.
- Ogni client mantiene un file di configurazione per ogni utente, con
possibilità di condivisione del file, in cui viene elencata una lista
ordinata di URL di gerarchie. Gli URL sono ordinati secondo l'ordine di
preferenza crescente dell'utente per i vari server. Questa scelta corrisponde
alla politica più semplice che soddisfa il primo requisito obbligatorio:
l'ordinamento fra i server è totale e indipendente dall'URI particolare.
Anche in questo caso il formato del file può essere ragionevolmente sia
testuale che XML. Il numero degli elementi della lista, però, sarà
sempre ragionevolmente basso e saranno sicuramente implementati in futuro
vari tipi di elaborazioni sul file, quali modifiche, confronti, fusioni
e riordinamenti. Pertanto, la scelta cade ragionevolmente sul formato XML,
anche se, per il momento, l'implementazione utilizza un semplice file
testuale3.
- Ogni client mantiene, per ogni file di configurazione, un semplice
database con una sola tabella in cui ad ogni URI viene associato l'URL
ottimale, scelto in accordo con l'ordinamento del file. L'unica query
possibile sul database è la richiesta di quale URL è associato ad
un determinato URI. La struttura del database e la forma della query
suggeriscono fortemente l'adozione come database di un file Berkeley DB,
che a sua volta è usualmente implementato come un BTree e che è uno
standard consolidato in ambiente Unix, ma di cui esistono implementazioni
anche sotto altri sistemi operativi (es. Microsoft).
- Vengono forniti tre moduli OCaml, il cui grafo delle dipendenze
è mostrato in figura 4.1
Figura 4.1: Grafo delle dipendenze per i moduli dell'implementazione del getter come modulo OCaml
Il primo modulo, chiamato UriManager,
fornisce il tipo di dato astratto uri, la funzione eq
per determinare l'uguaglianza fra uri e due funzioni di conversione fra il
tipo di dato astratto e la sintassi concreta, chiamate string_of_uri
e uri_of_string. La signature del modulo è la seguente:
type uri
val eq : uri -> uri -> bool
val uri_of_string : string -> uri
val string_of_uri : uri -> string
Il secondo modulo, chiamato Configuration, ha la seguente signature:
val tmpdir : string
val indexname : string
val servers_file : string
val uris_dbm : string
val dest : string
dove servers_file è il path assoluto del file descritto al punto
3, uris_dbm quello del file Berkeley DB descritto al punto 4,
indexname il nome del file descritto al punto 2, dest
il path del cache e tmpdir il path del directory da utilizzare
per la creazione di file temporanei. Il modulo deve essere implementato in
modo da leggere i parametri da un file XML specificato in qualche modo
dall'utente.
Il terzo modulo, chiamato Getter e dipendente dai precedenti, fornisce
esclusivamente l'implementazione dei due metodi update e
get, basata sulle decisioni prese nei precedenti punti. La signature
del modulo è la seguente:
(* get : uri -> filename *)
val get : UriManager.uri -> string
(* synchronize with the servers *)
val update : unit -> unit
Il metodo update si occupa di rigenerare il database contattando tutti i
server elencati nel file di configurazione. Il metodo get cerca in cache
il file il cui URI viene dato come parametro. Se non lo trova, lo scarica
utilizzando l'URL a cui l'URI è associato nel database e ne mette una
copia in cache. In entrambi i casi ritorna il path assoluto del file in
cache.
Si noti che, se il client è anche un server e il cache del client coincide
con la gerarchia esportata, diventa possibile mettere a disposizione tutti i
documenti acceduti semplicemente aggiungendo all'indice dei file
esportati ogni file scaricato dal getter.
Implementazione
Accenniamo ai punti salienti dell'implementazione di due dei tre moduli OCaml,
in quanto il restante, l'UriManager, non è interessante ai fini del modello
di distribuzione e può essere implementato in modo banale istanziando il
tipo di dato astratto con il tipo string, la funzione di confronto con
l'uguaglianza polimorfa del linguaggio e le due funzioni di conversione con
l'identità sulle stringhe4.
Per quanto riguarda il file di configurazione, si è scelto di utilizzare
un file XML, di cui è stato fornito il DTD, avente per ogni parametro un
elemento il cui nome sia lo stesso del parametro.
Inoltre, per evitare di replicare più volte le stesse sotto-stringhe,
è possibile utilizzare un elemento XML, il cui tag è ``value-of'',
per effettuare interpolazione della variabile già definita il cui nome è
indicato nell'attributo ``var''.
Il modulo Configuration è stato
quindi implementato ricorrendo a Markup5, un parser XML validante
con ottime prestazioni6 implementato interamente in OCaml.
Il modulo Getter è stato implementato nella maniera più scontata, ricorrendo
alla libreria standard di OCaml per la gestione dei file Berkeley DB e
richiamando il programma wget7 per effettuare il download di un
file dato l'URL. Vediamo più dettagliatamente le operazioni compiute dalle
due funzioni:
-
update
- Vengono scaricati, utilizzando wget, gli indici dei file esportati
di tutti i server specificati dall'utente e letti dall'apposito file.
A questo punto si svuota il database e, partendo dall'ultimo indice scaricato
e procedendo a ritroso, si inseriscono nel database tutte le coppie URI---URL
per le quali non è già stata inserita una coppia con lo stesso URI.
- get
- A partire dall'URI dato in input, si ricava il pathname del file
in cache che sarà il valore ritornato. Se il file è già lí presente,
la funzione termina; altrimenti, si ricava dal database l'URL da contattare
e si usa wget per scaricare il file.
Il codice, anche grazie all'utilizzo di wget e Markup, risulta molto compatto:
il modulo Getter richiede solo 111 righe di codice OCaml, commenti inclusi
(99 senza commenti); Configuration 90 righe (76 senza commenti);
l'implementazione banale di UriManager solo 3 righe prive di commenti.
L'intera implementazione ha richiesto meno di un pomeriggio (5 ore uomo).
4.1.2 Il getter con interfaccia HTTP
Il secondo prototipo sviluppato viene richiamato dagli stylesheet descritti
nel capitolo 6 quando è necessario accedere ad altri
documenti,
per esempio per conoscere i nomi dei costruttori dato l'URI, l'indice
della definizione (co)induttiva del loro tipo e l'indice del costruttore.
Poiché non esiste una maniera standard per estendere i processori XSLT
con moduli per la risoluzione degli URI, si è scelto di fornire una
seconda implementazione del getter sotto forma di (mini) server HTTP.
Una soluzione alternativa era l'utilizzo di un CGI; questa, però,
obbligava l'utente all'installazione di un server Web, di norma di
cospicue dimensioni, che fornisse il supporto per i CGI. La nostra
implementazione, al contrario, è caratterizzata dalla modestissima
occupazione in memoria e su disco (uno script Perl di sole 183 righe,
commenti inclusi).
Il mancato riutilizzo del modulo OCaml è ben motivato: poiché in OCaml non
esiste alcuna libreria che implementi le funzionalità di un server
HTTP, la complessità della realizzazione della libreria sarebbe stata
ampiamente maggiore di quella della reimplementazione in un altro linguaggio.
Inoltre, per motivi di efficienza, non è stato nemmeno possibile invocare
il primo prototipo come programma esterno: questo, dopo aver scaricato un file,
lo memorizza su disco con conseguente necessità di ricaricarlo in memoria
per restituirlo al client HTTP8.
Progettazione
Anche in questo caso la progettazione, che si è pesantemente basata su
quella del primo prototipo, è stata estremamente semplice.
Si è deciso che:
-
Il file di configurazione, quello in cui vengono elencati i siti
da contattare, il database e il cache su disco sono condivisi con il primo
prototipo.
- Il prototipo si comporta come un server HTTP, mettendosi in
ascolto su una porta specificata dall'utente e rispondendo alle
richieste i cui percorsi (ovvero la parte dell'URL che segue quella
che identifica l'host) sono istanze dei seguenti schemi:
-
/get?url=uri Utilizzato per chiedere
una copia del documento il cui URI è uri.
- /annotation?url=uri Descritto nel capitolo 6
- /getdtd?url=nome Utilizzato per ottenere una
copia del DTD il cui nome è nome9.
- /conf Utilizzato per sintetizzare un documento XML contenente
alcuni dei parametri di configurazione del getter.
Per esempio, per richiedere la definizione del tipo induttivo dei numeri
naturali al getter che gira sulla porta 8081 dell'host phd.cs.unibo.it,
si utilizza il seguente URL:
``http://phd.cs.unibo.it:8081/get?uri=cic:/coq/INIT/Datatypes/nat.ind''
- Il getter è implementato ricorrendo a due moduli Perl, dei quali
uno è responsabile esclusivamente della gestione dei parametri di
configurazione.
Implementazione
L'implementazione è stata estremamente banale grazie all'utilizzo delle
seguenti librerie Perl:
-
HTTP::Daemon che implementa un semplice server HTTP che è
facilmente personalizzabile scrivendo il codice che viene richiamato ogni
volta che viene effettuata una chiamata al server. La libreria, inoltre,
facilita la manipolazione di tutti i parametri, sia in entrata che in uscita,
della richiesta HTTP.
- LWP:UserAgent che implementa un client HTTP, gestendo tutti
i dettagli della connessione.
- DB_File che è una libreria per la gestione di vari tipi di
database implementati come file, fra cui quelli Berkeley DB.
- XML::Parser che implementa un semplice parser XML fornendo
un'interfaccia ad eventi simile a SAX10.
Scendendo maggiormente in dettaglio, sono stati implementati due script Perl,
configuration.pl e http_getter.pl. Il primo copre lo
stesso ruolo del modulo OCaml Configuration, esportando omonime
variabili. Il secondo, che utilizza il primo, implementa il server HTTP:
ogni volta che viene ricevuta una richiesta, controlla se questa rientra in
uno degli schemi di URL riconosciuti e11
-
se la richiesta è di tipo conf, restituisce un documento
XML creato al volo in cui vengono indicati alcuni dei propri parametri
di configurazione.
- se la richiesta è di tipo getdtd, carica il DTD richiesto
da disco e lo restituisce.
- se la richiesta è di tipo get, effettua le stesse operazioni
eseguite dal metodo get del modulo Getter del primo prototipo; invece di
restituire il nome del file, però, restituisce il contenuto del file
scaricato o, se questo era già presente in cache, il contenuto della copia
in cache.
Il codice, grazie all'utilizzo delle potenti librerie elencate precedentemente,
è molto compatto: il modulo configuration.pl è di sole 35 linee, commenti
inclusi; http_getter.pl è di 183 linee commenti inclusi (175 senza commenti).
L'intera implementazione ha richiesto due giorni (20 ore uomo), incluso il
tempo dedicato allo studio di alcune delle librerie.
- 1
- L'affermazione deve
essere mitigata. Nel caso in cui il server sia a sua volta un sistema
distribuito con bilanciamento del carico e replicazione in spazio, i
problemi citati non si presentano. Attualmente, però, la maggior
parte degli utenti ha accesso esclusivamente a sistemi non fault-tolerant
costituiti da un singolo host, per cui vale l'affermazione.
- 2
- http://www.debian.org
- 3
- Il passaggio al formato XML dovrebbe avvenire a breve.
- 4
- Per una implementazione nient'affatto
banale data durante lo sviluppo del proof-checker, si veda il paragrafo
5.1.1.
- 5
- http://www.ocaml-programming.de/packages/documentation/pxp
- 6
- Nel solo parsing di tutti i
file XML che compongono la libreria standard di Coq, Markup è risultato
circa 5 volte più veloce del parser validante per SGML scritto in C da
J. Clark e chiamato SP (SGML Parser) e ha avuto approssimativamente le stesse
prestazioni di expat che è un parser XML non validante scritto in C sempre
da J. Clark.
- 7
- wget è un utility free, sviluppato
dal consorzio GNU, per il download non interattivo di singole pagine o di interi
siti. Può utilizzare indistintamente i protocolli HTTP o FTP.
- 8
- Il server potrebbe efficientemente
restituire al client la locazione su disco del documento, in conformità al
protocollo HTTP. Questa opzione non è , però, possibile, in quanto
il prototipo, come descritto nel capitolo 6, effettua
anche sintesi al volo di file ottenuti a partire da più di un documento alla
volta.
- 9
- I DTD in HELM non
vengono identificati da un URI, ma semplicemente dal loro nome.
- 10
- SAX è un'interfaccia ad
eventi per i parser XML che è diventata uno standard di fatto in
ambiente Java.
- 11
- Le operazioni compiute se la
richiesta è di tipo annotation verranno descritte nel
capitolo 6.
Chapter 5 Un proof-checker per i file CIC della libreria
In questo capitolo descriveremo brevemente la progettazione e l'implementazione
di un proof-checker per i file CIC della libreria di HELM. Entrambe non sono
ancora state completate, in quanto non è stata ancora considerata la
stratificazione degli universi, ovvero tutti i Type(i) sono
rappresentati da Type1. Il
proof-checker verrà completato quanto prima, probabilmente entro la fine
del 2000.
Le motivazioni dello sviluppo del proof-checker sono molteplici:
-
La scrittura del proof-checker ha permesso di determinare se tutta
l'informazione degli oggetti CIC è stata esportata.
- Il proof-checker rappresenta la dimostrazione concreta della possibilità
di reimplementare tutte le funzionalità dei moderni proof-assistant
monolitici in maniera modulare, basandosi sul formato XML.
In particolare, l'architettura
e l'implementazione risultanti sono estremamente più semplici ed eleganti
di quelle del proof-checker integrato in Coq. Inoltre, nonostante il codice
non sia stato particolarmente ottimizzato e gli algoritmi adottati siano fra
i più semplici noti, le prestazioni del proof-checker sono comparabili a
quelle di Coq, se si escludono le rispettive fasi di parsing.
- A partire da una implementazione completa e funzionante del proof-checker,
diventa possibile sperimentare modifiche al sistema logico, per esempio per
affrontare il problema delle dimensioni delle prove.
- Alcune sottigliezze del sistema logico possono essere comprese solamente
durante la progettazione e l'implementazione di un proof-checker, che
assumono, quindi, importanti valenze didattiche.
Inoltre, il nostro proof-checker è il primo, a conoscenza degli autori, a
gestire dinamicamente gli ambienti, utilizzando esclusivamente l'ordinamento
parziale generato dalle dipendenze fra gli oggetti (vedi pagina
59).
Sono state prese due importanti decisioni preliminari alla progettazione.
La prima è sull'obiettivo dello sviluppo, che è mirato all'ottenimento
di un prototipo. Pertanto,
la performance viene tenuta in secondo piano rispetto alla pulizia
dell'architettura e alla semplicità dell'implementazione. Ciò nonostante,
i risultati ottenuti sono stati decisamente buoni, anche sul piano delle
prestazioni.
La seconda decisione riguarda la scelta del linguaggio di programmazione:
l'intero proof-checker è sviluppato in OCaml. Il linguaggio si è già
dimostrato ottimale nell'ambito dello sviluppo di
type-checker. Infatti, i tipi di dati concreti di OCaml permettono una
definizione compatta ed elegante della sintassi di CIC, mentre il
paradigma funzionale e il garbage collector rendono concisa l'implementazione
e permettono di definire funzioni aderendo strettamente alle regole
di tipaggio date nel capitolo 2.1. Il fatto che anche Coq sia
implementato in OCaml semplifica il riutilizzo del codice2.
Inoltre, l'estrema concisione della sintassi di OCaml, dovuta
principalmente alla type-inference, e la caratteristica del linguaggio di
essere fortemente tipato rendono la produttività in fase di implementazione
mediamente molto alta, con un numero quasi nullo di errori di tipo non
logico. Il complesso sistema di moduli del linguaggio permette
di sfruttare moderne tecniche di ingegneria del software usualmente
applicabili quasi esclusivamente nell'ambito dei linguaggi ad oggetti.
Infine, per quei compiti per i quali il paradigma funzionale non è
maggiormente adatto o è poco conciso, è possibile utilizzare feature
imperative e, quando il sistema dei moduli si rivela insufficiente,
ricorrere agli oggetti, che possono essere utilizzati sia in maniera
funzionale che imperativa.
Nelle successive due sezioni descriveremo brevemente rispettivamente
la progettazione e l'implementazione del prototipo. Si assume non solo
un'ottima comprensione dell'intera sezione 2.1 che descrive CIC
e dei paragrafi 2.2.1, 2.2.2 e 2.2.4
che descrivono le estensioni di Coq, ma anche una buona conoscenza
sull'implementazione di type-checker per l-calcoli basati sulla
rappresentazione delle variabili con indici di DeBrujin.
5.1 Progettazione
Figura 5.1: Grafo delle dipendenze per i moduli dell'implementazione
del typechecker
In figura 5.1 viene mostrato il grafo delle dipendenze dei
moduli del typechecker, cosí come deciso in fase di progettazione.
La buona norma di evitare dipendenze cicliche fra moduli non può essere
violata in OCaml. Pertanto, già in fase di progettazione, è bene
discriminare le dipendenze in statiche e dinamiche per eliminare i cicli.
Una freccia solida da un modulo A verso un modulo B significa che A
dipende staticamente, ovvero in fase di compilazione, da B. Una freccia
tratteggiata da A verso B, invece, indica una dipendenza dinamica: a
run-time il modulo B registrerà una o più sue funzioni presso il modulo
A affinché questo le richiami3. Tutti i
moduli racchiusi in un rettangolo tratteggiato dipendono direttamente da tutti
i moduli che sono bersaglio di una freccia con sorgente il riquadro. Il
simbolo formato con rettangoli sovrapposti indica un metamodulo, ovvero un
modulo logico che è a sua volta decomposto in altri moduli logici. In
particolare, il metamodulo getter è già stato descritto nel
capitolo 4.1.1, dove in figura 4.1 sono state indicate le
dipendenze fra i moduli logici che lo compongono.
Passiamo ora a descrivere individualmente i singoli (meta)moduli.
5.1.1 UriManager
È un sotto-modulo, nel senso dell'ereditarietà nei linguaggi ad oggetti,
di quello descritto nel paragrafo 4.1.1;
pertanto, una sua implementazione
può sostituire quella dell'omonimo modulo nel metamodulo Getter. Lo scopo
del modulo è fornire un tipo di dato astratto uri con le relative
operazioni richieste durante l'implementazione del type-checker. La sua
interfaccia, o signature, è:
type uri
val eq : uri -> uri -> bool
val uri_of_string : string -> uri
val string_of_uri : uri -> string (* complete uri *)
val name_of_uri : uri -> string (* name only (without extension)*)
val buri_of_uri : uri -> string (* base uri only *)
val depth_of_uri : uri -> int (* length of the path *)
(* relative_depth curi uri cookingsno *)
(* is the number of times to cook uri to use it when the current *)
(* uri is curi cooked cookingsno times *)
val relative_depth : uri -> uri -> int -> int
I primi quattro elementi sono gli stessi già descritti nel paragrafo
4.1.1.
Le successive tre funzioni sono di uso frequente. L'ultima è
tecnica e verrà richiamata dal meccanismo di cottura: restituisce il numero
di volte che un oggetto di cui viene specificato l'URI deve essere cucinato
per essere utilizzato durante il type-checking di un altro oggetto di cui
viene indicato l'URI e il numero di cotture subite. Con ``numero di cotture'',
a differenza di quanto accade in Coq, non indichiamo il numero di ingredienti
astratti, bensí la differenza fra la lunghezza dell'URI dell'oggetto
prima e dopo la cottura. Quest'uso è coerente con l'osservazione che un
oggetto viene sempre cucinato rispetto a tutti o nessuno degli ingredienti
definiti in una stessa sezione.
Raffinamento della specifica
Poiché gli URI vengono utilizzati pesantemente sia nella rappresentazione
interna dei l-termini, sia durante il type-checking, si impongono, per
motivi prestazionali, dei vincoli sia sulla complessità computazione delle
funzioni, sia sull'occupazione in spazio della rappresentazione degli URI:
-
Due URI identici devono condividere la stessa rappresentazione. In
altre parole, la uri_of_string, se richiamata due volte su
stringhe uguali, deve restituire in entrambi i casi la stessa (in senso fisico)
struttura dati.
- Le funzioni eq, string_of_uri, name_of_uri,
buri_of_uri e depth_of_uri devono appartenere a O(1).
- La funzione relative_depth deve appartenere a
O(depth_of_uri(u)) dove u è l'URI dato in input.
Per ottenere complessità computazionali cosí basse diventa necessario
ricorrere a una rappresentazione degli URI decisamente elaborata. Come
conseguenza, è lecito aspettarsi un'alta complessità computazionale
per la uri_of_string. Ciò nonostante, poiché capita
frequentemente che, durante il proof-checking di un oggetto, si incontri lo
stesso URI più volte, viene richiesto un ulteriore vincolo sulla complessità
di tale funzione:
-
La complessità computazionale media della depth_of_uri su
un URI già incontrato deve essere al più O(log(n)) dove n è il
numero di URI già incontrati.
5.1.2 Cic
Questo modulo, privo di funzioni, fornisce esclusivamente la rappresentazione
concreta dei termini e degli oggetti di CIC. La sua signature viene interamente
riportata, per comodità di consultazione, in appendice B.
Confrontando attentamente la rappresentazione XML in appendice
A con quella OCaml e con la sintassi di CIC descritta nel
paragrafo 2.1.1, si individuano facilmente le seguenti
discrepanze4:
-
Lo zucchero sintattico è scomparso, riavvicinandosi alla
rappresentazione data nella descrizione della teoria.
In particolare, i binder, che nella
rappresentazione XML erano stati spostati sull'elemento target, sono
tornati ad essere attributi di Lambda o Prod.
- Tutti gli URI, che in XML erano in parte assoluti e in parte relativi,
hanno la stessa rappresentazione interna, determinata dal modulo UriManager.
- Tutti gli URI che si riferiscono ad oggetti cucinabili hanno sempre
associato un indice, indicato in commento con cookingsno, che
indica il livello di cottura voluto per l'oggetto. Questo deve essere
calcolato durante il parsing e modificato ad ogni cottura dell'oggetto.
Il motivo che ci ha spinto ad esplicitare l'indice, che poteva comunque essere
calcolato al volo all'occorrenza, è dovuto alla complessità computazione
dell'operazione, che, pur non essendo troppo elevata (vedi paragrafo
5.1.1), diventava influente per l'alto numero di applicazioni
della funzione relative_depth che sarebbero state richieste.
- La rappresentazione interna degli ingredienti di un oggetto è una
buona sintesi, in termini di efficienza, fra quella dei file XML e quella
come lista di coppie. In pratica, è una lista di liste di URI avente un
elemento per
ogni token numerico presente nel file XML, ovvero per ogni livello di cottura;
la lista elemento contiene tutti gli URI degli ingredienti per quel livello.
- La rappresentazione OCaml dei costruttori prevede un ulteriore parametro,
assente sia nella teoria che nel DTD XML, che è un reference ad una
lista di booleani, possibilmente non specificata: durante il parsing, la
lista non viene specificata; durante il proof-checker del tipo induttivo del
costruttore, vengono individuati i parametri in cui il costruttore è
ricorsivo, nel senso del paragrafo 2.10, e l'informazione viene
memorizzata nella lista di booleani per essere poi utilizzata più volte
durante le verifiche delle condizioni GC e GD, con
conseguente incremento delle prestazioni.
5.1.3 CicParser
Il compito di questo metamodulo è semplicemente quello, dato un file
XML che descrive un oggetto CIC, di restituirne la rappresentazione interna.
Pertanto, la sua signature è formata da una sola funzione:
val term_of_xml : string -> UriManager.uri -> Cic.obj
dove il primo parametro è il pathname del file XML e il secondo il suo URI,
necessario per risolvere gli URI relativi durante il parsing.
Raffinando la progettazione, si è deciso di implementare il metamodulo
utilizzando tre distinti moduli, chiamati CicParser, CicParser2, CicParser3.
Il primo ha il compito di costruire l'albero di sintassi astratta associato
al file XML5; il secondo si occupa della creazione, a partire
da questo, della rappresentazione interna a livello degli oggetti; il terzo
fa lo stesso, ma a livello dei termini. Nella sezione dedicata
all'implementazione si mostrerà il grafo delle dipendenze fra i moduli e
si accennerà brevemente alle signature degli ultimi due.
5.1.4 CicCache
Questo è sicuramente il modulo dall'interfaccia più complessa.
I suoi compiti principali sono quello di fungere da cache per incrementare
le prestazioni nell'accesso agli oggetti e quello di nascondere l'utilizzo
del Getter e del CicParser ai moduli dei livelli soprastanti.
Poiché il parsing dei file XML
è un'operazione molto costosa in termini di tempo, il cache deve evitare
il più possibile un cache miss, eliminando gli elementi esclusivamente
quando strettamente necessario. Il parsing non è, però, la sola operazione
critica compiuta sugli oggetti: la loro cottura, infatti, richiede la visita
esaustiva dei loro termini e l'accesso a tutti gli oggetti in essi riferiti.
Pertanto, dopo aver sviluppato un primo prototipo del proof-checker in cui
la cottura veniva effettuata al volo, abbiamo deciso di mantenere in cache
non solo la versione meno cucinata di un oggetto, ma anche tutte quelle
parzialmente o totalmente cotte, ottenendo un sensibile incremento delle
prestazioni. La decisione, però, introduce una inevitabile circolarità
fra le operazioni di accesso al cache, cottura e type-checking: un oggetto
può essere cucinato esclusivamente se ha già superato il proof-checking;
per il suo type-checking e la cottura, però, è necessario utilizzare
il cache per ottenere la definizione dell'oggetto e di quelli da questo
riferiti. Il punto chiave che ha permesso di risolvere, in parte, la
circolarità sono le seguenti osservazioni, derivate da una semplice analisi
delle regole di tipaggio di CIC e da quelle di introduzione di oggetti
nell'ambiente:
-
Il grafo diretto delle dipendenze fra gli oggetti di CIC è
aciclico6.
- Anche se la riduzione è definita per termini qualsiasi, ai fini
del proof-checking può essere sempre richiamata esclusivamente su termini
che abbiano già superato il type-checking.
Come conseguenza, è possibile definire il cache in modo che mantenga
gli oggetti in una delle seguenti tre forme: non cucinata e non
type-checked, congelata, cucinata a tutti i livelli possibili. Quando il
termine viene richiesto per la prima volta, lo si scarica ricorrendo al
getter e se ne ottiene la forma non cucinata e non type-checked utilizzando
il parser. Per effettuarne il type-checking, si deve comunicarne l'intenzione
al cache, che passerà l'oggetto alla forma congelata, ma, quando richiesto,
continuerà a restituirlo nella forma precedente. Infine, la terminazione del
type-checking deve essere comunicata al cache, che invoca il meccanismo di
cottura per ottenere lo stesso oggetto cucinato ad ogni possibile livello,
passandolo alla terza forma. Solo da questo momento in avanti sarà possibile
accedere alle forme cucinate.
Il meccanismo appena descritto permette di risolvere elegantemente la
dipendenza circolare fra il type-checker e il modulo responsabile della
cottura e quella fra il type-checker e il cache, ma non elimina quello
fra il modulo di cottura e il cache. Poiché il cache non dovrebbe avere,
almeno intuitivamente, alcuna dipendenza dal meccanismo di cottura, che è
strettamente dipendente dal sistema logico, diventa naturale mantenere la
dipendenza statica fra il modulo di cottura e il cache, rendendo dinamica
quella in senso opposto.
Considerate tutte le precedenti osservazioni, si è scelta la seguente
signature per il modulo, dove il costruttore delle forme congelate viene
tenuto nascosto grazie ai meccanismi di information hiding di OCaml:
exception CircularDependency of string;;
(* get_obj uri *)
(* returns the uncooked form of the cic object whose URI is uri. *)
(* If the term is not just in cache, then it is parsed via *)
(* CicParser.term_of_xml from the file whose name is the result *)
(* of Getter.get uri *)
val get_obj : UriManager.uri -> Cic.obj
type type_checked_obj =
CheckedObj of Cic.obj (* cooked obj *)
| UncheckedObj of Cic.obj (* uncooked obj *)
(* is_type_checked uri cookingsno *)
(* returns (CheckedObj object) if the object has been *)
(* type-checked otherwise it returns (UncheckedObj oject) and *)
(* freeze the object for the type-checking *)
(* set_type_checking_info must be called to unfreeze the object *)
val is_type_checked : UriManager.uri -> int -> type_checked_obj
(* set_type_checking_info uri *)
(* must be called once the type-checking of uri is finished *)
(* The object whose URI is uri is unfreezed and cooked at every *)
(* possible level using the !cook_obj function *)
(* Therefore, is_type_checked will return a CheckedObj *)
val set_type_checking_info : UriManager.uri -> unit
(* get_cooked_obj uri cookingsno *)
(* returns the object whose URI is uri cooked cookingsno levels *)
val get_cooked_obj : UriManager.uri -> int -> Cic.obj
val cook_obj :
(Cic.obj -> UriManager.uri -> (int * Cic.obj) list) ref
Il significato di tutte le funzioni dovrebbe essere chiaro grazie ai commenti
e alle spiegazioni precedenti. La cook_obj è la reference
con la quale deve essere registrata la funzione di cottura che, dato un oggetto
nella forma non cucinata e il suo URI, ritorna una lista di coppie livello di
cottura---oggetto cucinato a quel livello.
5.1.5 CicCooking
La signature del modulo CicCooking è composta da una sola funzione che
viene registrata presso il cache durante l'inizializzazione del modulo stesso:
val cook_obj : Cic.obj -> UriManager.uri -> (int * Cic.obj) list
La funzione deve semplicemente implementare fedelmente le regole di cottura
date informalmente nel paragrafo 2.2.4.
5.1.6 CicSubstitution, CicReduction e CicTypeChecker
Questi moduli non hanno richiesto alcuno sforzo progettuale, in quanto
sono assolutamente standard nella scrittura di type-checker per
l-calcoli, a partire da quello tipato semplice. Chi conosce questi
strumenti dovrebbe riconoscere immediatamente le funzioni descritte nelle
signature dei tre moduli:
CicSubstitution:
val lift : int -> Cic.term -> Cic.term
(* subst t1 t2 substitutes t1 for the first free variable in t2 *)
val subst : Cic.term -> Cic.term -> Cic.term
CicReduction:
val whd : Cic.term -> Cic.term
val are_convertible : Cic.term -> Cic.term -> bool
CicTypeChecker:
exception NotWellTyped of string
val typecheck : UriManager.uri -> unit
5.2 Implementazione
In questa sezione si accennerà brevemente all'implementazione del
proof-checker, descrivendo esclusivamente le scelte implementative
non standard o quelle che hanno avuto grossi impatti dal punto di
vista delle prestazioni. I moduli verranno descritti singolarmente,
nello stesso ordine della precedente sezione. Infine, verranno
riportate alcune statistiche.
5.2.1 UriManager
Sono state fornite tre differenti implementazioni, che
utilizzano strutture dati di complessità crescente.
All'aumento di complessità corrisponde, in teoria, un aumento del
tempo richiesto per il primo accesso e una sua diminuzione per gli
accessi successivi. Concretamente, però, nessuna delle tre soluzioni ha
dato risultati superiori alle altre in tutti i casi: per teorie semplici,
con pochi riferimenti fra oggetti, le soluzioni più semplici danno
risultati lievemente migliori; per quelle complesse, si ha il fenomeno opposto.
Effettuando statistiche sul proof-checking di tutta la libreria standard di
Coq, che contiene due teorie complesse di notevoli dimensioni, quella dei
numeri reali e quella della normalizzazione di espressioni su anelli, si è
riscontrato un iniziale aumento delle prestazioni passando dall'implementazione
più semplice a quella più complessa di circa il 15%, che si
è poi ridotto notevolmente in seguito alle ottimizzazioni successivamente
introdotte nella cicReduction. Pertanto, si è preferito mantenere
esclusivamente l'implementazione più complessa, che ora descriveremo, che
è anche l'unica che rispetta pienamente i vincoli sulla complessità
computazionale introdotti in fase di progettazione nel paragrafo
5.1.1.
Ogni URI viene rappresentato internamente come un vettore contenente, in ordine
lessicografico, tutti i suoi URI prefisso, seguiti dal nome dell'oggetto.
Per esempio, l'URI ``cic:/a/b/c.con'' viene codificato con il
vettore [| "cic:/a" ; "cic:/a/b" ; "cic:/a/b/c.con" ; "c" |].
Questa rappresentazione permette di ottenere sia la lunghezza di un URI
che il nome dell'oggetto da esso riferito in O(1). Per implementare la
uri_of_string, viene utilizzato un albero bilanciato di ricerca
che implementa una funzione che mappa ogni URI in formato stringa nella
rappresentazione interna: ad ogni invocazione della funzione, l'URI viene
cercato nell'albero e restituito; solo se non presente, viene creata la sua
rappresentazione interna, memorizzata nell'albero e restituita come valore di
ritorno. In questo modo, come funzione eq per l'uguaglianza fra URI
può essere utilizzata direttamente l'uguaglianza fisica di OCaml, che
appartiene a O(1) in quanto si limita a confrontare l'indirizzo in memoria dei
due valori. Lo stesso stratagemma viene utilizzato per normalizzare i prefissi
utilizzati nella rappresentazione interna, ricorrendo ad un secondo albero
bilanciato di ricerca. A parte l'ovvio risparmio in spazio, è in questo modo
possibile implementare la relative_depth iterando in parallelo
sulle rappresentazioni interne dei due URI e utilizzando l'uguaglianza
fisica per confrontare fra loro i prefissi, riducendo la complessità
computazionale di tutta l'operazione, che diventa lineare nella profondità
dell'URI più breve. Come conseguenza negativa, il caso pessimo della creazione
di un nuovo URI diventa O(n2 + log m), dove n è la lunghezza in
caratteri dell'URI e m il numero di URI già incontrati. Un'analisi più
approfondita basata su un modello plausibile per la località dei riferimenti
nella libreria, però, rivela che è possibile stimare il costo ammortizzato
in solo O(k/k - 1 + log m) dove k è il numero medio di oggetti
contenuti non ricorsivamente in ogni sezione.
5.2.2 CicParser
Il metamodulo, come preannunciato, è stato implementato ricorrendo a tre
moduli il grafo delle cui mutue dipendenze è riportato in figura
5.2.
Figura 5.2: Grafo delle dipendenze per i moduli dell'implementazione
del CicParser
Il primo modulo contiene il codice necessario per interfacciarsi con Markup,
un parser XML scritto in OCaml; una volta ottenuto l'albero di sintassi
astratta da Markup, vengono richiamate le funzioni del secondo modulo.
Il terzo modulo
prende in input un albero di sintassi astratta di Markup relativo ad un termine
e ne ritorna la rappresentazione interna, di tipo Cic.term.
Il secondo, che richiama il terzo, fa lo stesso per gli oggetti.
La dipendenza statica e quella dinamica fra il primo modulo e il terzo
sono dovute a dettagli implementativi sull'utilizzo di Markup, che espone
due interfacce, una ad oggetti e una funzionale pura; il secondo modulo
ricorre a quella funzionale pura, il terzo a quella ad oggetti. I motivi
della scelta dell'utilizzo di entrambi i tipi di interfacce sono dovuti
al trade-off fra complessità computazionale e spaziale: l'interfaccia ad
oggetti diminuisce la prima grazie all'uso del late binding, ma richiede
la creazione di un nuovo oggetto per ogni nodo dell'albero di sintassi
astratta; quella funzionale non deve istanziare oggetti, ma è costretta
ad effettuare ripetuti e costosi confronti fra stringhe per discriminare i
tag dei nodi dell'albero. L'alto numero di elementi XML per il markup a livello
dei termini suggerisce l'adozione dell'interfaccia ad oggetti per minimizzare
il tempo di parsing. Il basso numero di elementi per il livello degli oggetti
determina un basso costo computazionale anche per l'interfaccia funzionale, che
non è, però, soggetta ad ulteriore costo spaziale, rendendola preferibile.
5.2.3 CicCache
L'unica osservazione di rilievo è il fatto che, almeno in questa prima
implementazione, si
è deciso di non eliminare mai un oggetto dal cache. Infatti, l'occupazione
complessiva di memoria del proof-checker dopo la verifica di tutti gli oggetti
della libreria standard di Coq è ancora sufficientemente bassa da non
giustificare lo sforzo implementativo.
5.2.4 CicCooking
Sull'implementazione del meccanismo di cottura, sono necessarie
due osservazioni. La prima è legata alla differente rappresentazione interna
dei tipi mutuamente (co)induttivi rispetto alla descrizione teorica. Come
descritto nel paragrafo 2.2.2, le occorrenze dei tipi (co)induttivi
all'interno dei tipi dei loro costruttori vengono rappresentate da indici di
de Brujin. Tali indici, quindi, si riferiscono ad oggetti cucinabili presenti
nell'ambiente, che possono avere ingredienti. Conseguentemente,
l'implementazione naïf della cottura diventa complessa, con la necessità
di mantenere un contesto di cottura in cui agli indici di de Brujin vengono
associati gli ingredienti richiesti dalle ``entità'' a cui essi puntano.
Per ovviare al problema, è possibile utilizzare un diverso formato interno
in cui anche le occorrenze dei tipi (co)induttivi all'interno dei tipi dei
rispettivi costruttori sono codificate come MutInd. Come conseguenza,
però, si avrebbe un aumento della complessità del type-checking. La
soluzione che abbiamo adottato consiste nell'utilizzare quest'ultima forma
esclusivamente per i termini cotti.
La prima operazione compiuta dalla funzione di cottura, quindi, diventa il
cambio di rappresentazione per il termine ancora non cucinato.
Il fatto che sia possibile far coesistere due diverse rappresentazioni senza
modificare le regole di tipaggio può, a prima vista, sembrare sorprendente.
Valutando attentamente la forma della regola Ind data a pagina
35 nella codifica con indici di de Brujin, però, si
nota che quello che viene fatto è semplicemente anticipare la sostituzione
che andrebbe effettuata ogni volta che la regola viene applicata.
La seconda osservazione sul meccanismo di cottura è legata alla scelta,
nella nostra rappresentazione interna, di associare ad ogni URI il numero di
volte che l'oggetto puntato deve essere cucinato. Cosí facendo, un oggetto
A che non dipenda da nessun ingrediente e l'oggetto A', ottenuto cucinando
A di un livello, differiscono nella rappresentazione interna esclusivamente
per tali indici. La conseguenza è la necessità di mantenere in cache
copie praticamente identiche degli oggetti, con enorme spreco di memoria dovuto
al fatto che, normalmente, un oggetto ha ingredienti solamente ad una piccola
percentuale dei livelli possibili. Riguardando attentamente la definizione
di cottura data nel paragrafo 2.2.4, è facile convincersi del seguente
fatto: gli ingredienti di un oggetto sono contenuti nell'insieme degli
ingredienti di ogni oggetto che da lui dipende. Come semplice corollario si ha
che, inserendo in cache l'oggetto A dell'esempio precedente al posto di A',
tutti gli oggetti che dipendono da A' supereranno il type-checking a patto
che la regola di conversione ignori gli indici; questo è esattamente ciò
che è stato implementato.
5.2.5 CicSubstitution, CicReduction
I moduli CicSubstitution e CicReduction sono stati implementati in maniera
naïf, con sostituzioni esplicite. Questo ha permesso al codice di essere
estremamente aderente alle definizioni formali, ma rende la whd,
ovvero la funzione che restituisce la forma normale di testa debole di un
termine, molto inefficiente: per esempio, per calcolare il fattoriale di 6,
la nostra implementazione impiega circa 2 minuti contro il secondo richiesto
da Coq. Lo scarso utilizzo della riduzione nelle dimostrazioni formali della
libreria di Coq7, però, annulla l'inefficienza, permettendoci di ottenere buone prestazioni.
La prima implementazione fornita, a dire il vero, era estremamente poco
soddisfacente dal punto di vista delle prestazioni. Un attento profiling ha
permesso di individuare la sorgente delle inefficienze nell'implementazione
della are_convertible, che decide la convertibilità di due termini.
In particolare, la funzione veniva richiamata la maggior parte delle volte
su termini identici, che venivano visitati interamente in maniera ricorsiva. Una
piccola euristica che abbiamo introdotto è il confronto preliminare dei due
termini, effettuato utilizzando l'uguaglianza polimorfa di OCaml, la cui
implementazione è molto efficiente. I risultati dell'applicazione di questa
semplice euristica sono stati stupefacenti: le prestazioni del proof-checking
dell'intera libreria standard di Coq sono state incrementate di circa dieci
volte.
5.2.6 CicTypeChecker
L'implementazione del type-checker è resa possibile dalla decidibilità
delle regole di tipaggio ovvero, in ultima analisi, dalle proprietà di
confluenza e normalizzazione forte di CIC. A causa della regola Conv, non
è possibile implementare direttamente le regole di tipaggio di CIC come
sono state date nel capitolo 2.1. In maniera del tutto standard,
viene definita una funzione privata, chiamata type_of, che
effettua contemporaneamente sia type-inference che type-checking, verificando
tutte le regole diverse dalla Conv e da quelle di introduzione degli oggetti
nell'ambiente. Una volta definita la type_of, la verifica
di t:T si riduce a quella type_of(t) =bdi T, ovvero
alla are_convertible(type_of(t),T)8. Le regole di introduzione degli oggetti
nell'ambiente sono implementate seguendo fedelmente le regole date nel
paragrafo 2.1.3, fermo restando il meccanismo appena descritto.
Quando, durante il type-checking di un oggetto, si incontra un
riferimento ad un oggetto non ancora presente in forma cucinata in cache,
si interrompe momentaneamente l'operazione sull'oggetto corrente e si
entra in ricorsione su quello riferito, sfruttando i meccanismi
messi a disposizione dal modulo CicCache e già descritti nel paragrafo
5.1.4.
5.2.7 Risultati ottenuti
L'implementazione complessiva del proof-checker ha richiesto circa
340 ore uomo; i tre moduli principali (CicSubstitution, CicReduction e
CicTypeChecker) sono stati sviluppati lavorando sempre in coppia; i restanti,
invece, singolarmente. Complessivamente sono state prodotte circa 3000 righe
di codice OCaml, escludendo quelle del metamodulo Getter, ma includendo la
nuova implementazione del modulo UriManager. Per effettuare il proof-checking
dell'intera libreria standard di Coq vengono richiesti mediamente 5 minuti e
47 secondi, incluso il tempo di parsing che è nell'ordine dei 5 minuti;
la prima implementazione richiedeva
circa 50 minuti. Non è possibile avere una stima precisa del tempo impiegato
da Coq, che è comunque sicuramente inferiore al minuto, parsing
incluso9.
I tempi, comunque, sono inevitabilmente destinati a salire con l'introduzione
della gestione del livello degli universi; una prima stima, però, indica
che l'incremento dovrebbe essere estremamente contenuto, non superando il
minuto.
- 1
- Come conseguenza immediata della
regola Ax-Acc si ha Type:Type; in presenza di questa
regola è ben nota (vedi [Coq86]) l'inconsistenza del sistema logico, nel
quale è possibile codificare un paradosso analogo a quello di Russel.
- 2
- Durante lo
sviluppo non è stato in effetti possibile riusare nessuna parte del codice
di Coq, principalmente a causa della rappresentazione interna di questo
basata sulla codifica di CIC come istanza di un metalinguaggio.
- 3
- Affinché B registri funzioni
presso A è necessario che B dipenda staticamente da A.
- 4
- Oltre a quella, già citata, sull'assenza della gestione
dei livelli degli universi, che sono espliciti nella sintassi di CIC, impliciti
nella rappresentazione XML, ma ancora assenti nella rappresentazione OCaml.
- 5
- Una possibile rappresentazione dell'albero è il DOM,
ovvero un API standard definito dal W3C. La natura tipicamente imperativa
di questo, però, si armonizza male in un linguaggio con feature imperative,
ma spirito funzionale quale OCaml. Pertanto, nessun parser XML per questo
linguaggio lo implementa, preferendogli un'API proprietario dalle
caratteristiche similari.
- 6
- Almeno nel caso delle costanti, è facile convincersi
dell'aciclicità: se questa venisse violata, esisterebbe una catena infinita
di d-espansioni; conseguentemente, il sistema non sarebbe fortemente
normalizzabile e, pertanto, nemmeno consistente. Nel caso dei tipi mutuamente
(co)induttivi, invece, l'argomento è più complesso, ma semplicemente a
causa della particolare formulazione di CIC proposta.
- 7
- Esistono due posizioni filosofiche sul ruolo della
riduzione nelle dimostrazioni formali. La prima cerca di evitarla il più
possibile, in quanto essa nasconde le motivazioni della correttezza delle
prove, che vengono basate esclusivamente sulla correttezza delle regole di
riduzione, ovvero sulla metateoria. La seconda la accetta sostenendo che,
una volta che ci si fidi della metateoria, le prove per riduzione non debbono
essere più comprese. Un esempio può chiarire il punto: si voglia provare
il teorema 2 + 3 = 3 + 2; una prima prova risulta immediata utilizzando
la proprietà commutativa dell'addizione; un metodo alternativo è
giustificare l'uguaglianza poiché entrambi i termini riducono a 5 e la
riduzione preserva l'uguaglianza di Leibniz: in questo caso, quindi, la prova
è immediata per la proprietà riflessiva dell'uguaglianza di Leibniz.
- 8
- È in questo momento che viene
utilizzata la regola Conv.
- 9
- Non bisogna dimenticare che il tempo richiesto dal parsing di
Coq è estremamente basso in quanto il formato dei file ``.vo'' è binario.
Chapter 6 La presentazione delle prove
Al fine di rendere comprensibili le dimostrazioni scritte sotto forma
di l-termini, è necessario affrontare due classi di problemi:
-
Problemi notazionali per le espressioni (tipi):
è necessario effettuare una
``rimatematizzazione'' delle espressioni formali, associando agli
operatori matematici la loro usuale notazione bidimensionale ed
astraendo dalla particolare definizione degli operatori nel sistema
logico, mantenendo però riferimenti precisi ai termini formali.
- Problemi di comprensibilità per le prove (termini):
è necessario associare ai termini che rappresentano prove nel
sistema logico una loro descrizione in linguaggio naturale, con
l'auspicabile possibilità di poter aumentare o diminuire il livello
di dettaglio della prova, fino a giungere al l-termine
sottostante (livello di dettaglio massimo).
Si noti che l'identificazione delle espressioni con i tipi e delle prove
con i termini, pur rappresentando l'essenza della moderna Teoria della
Dimostrazione, è solo approssimativa nei sistemi logici che prevedono
tipi dipendenti, come CIC: in questi sistemi, infatti, i termini e i
tipi sono generati dalla medesima produzione sintattica; ciò nonostante,
è comunque possibile in questi sistemi classificare tutti i
l-termini in livelli, fra i quali quello dei predicati e quello
delle prove, procedendo per ricorsione sulla struttura del termine (si
veda [Wer94]).
Nel prossimo paragrafo viene descritta l'architettura generale
utilizzata in HELM per affrontare entrambe le classi di problemi,
basata sulla tecnologia XSLT; si assume la conoscenza di XSLT da parte del
lettore.
Nel paragrafo 6.2 viene descritto in quale modo sono già stati
affrontati con un buon successo i problemi notazionali in HELM.
Per quanto riguarda la rappresentazione delle prove, come
già spiegato a pagina 8, non esistono attualmente
soluzioni
soddisfacenti; nel paragrafo 6.3 vengono rapidamente illustrate le
idee alla base dei tentativi che verranno effettuati nel successivo sviluppo
del progetto.
6.1 L'architettura generale delle trasformazioni presentazionali
Poiché tutti gli oggetti matematici sono salvati in formato XML
indipendentemente dal formalismo logico in cui sono definiti e in
conformità al prima requisito di HELM, tutte le trasformazioni fra
documenti XML, e in particolare quelle che associano ad un oggetto
la sua presentazione, vengono descritte in XSLT. Poiché ad ogni
formalismo viene associato un differente DTD XML, è richiesto uno
stylesheet presentazionale per ogni formalismo. Inoltre,
al fine di prevedere più di un formato di output e lasciare all'utente
la scelta di quello effettivamente utilizzato, è
richiesto uno stylesheet presentazionale per ogni formato di output.
Al fine di mantenere il numero degli stylesheet lineare nel numero dei
formati di input e output, è necessario adottare un formato intermedio
per disaccoppiare gli stylesheet di backend da quelli di frontend; come
già anticipato nel paragrafo 1.4, MathML content è il candidato
ottimale per questo compito in quanto mette a disposizione un linguaggio
standard per una descrizione semi-formale, ovvero già rimatematizzata,
delle espressioni matematiche.
In figura 6.1
viene mostrato lo schema globale delle trasformazioni XSLT.
Figura 6.1: Architettura generale delle trasformazioni presentazionali
I riquadri sulla sinistra indicano i tipi di documenti XML in input,
uno per ogni formalismo logico. Ogni documento prevede due tipi di markup,
quello del livello degli oggetti e quello del livello dei termini; le linee
tratteggiate che li separano nella figura ricordano il fatto che i due markup
sono presenti nello stesso documento e non sono distinti tramite namespace
differenti.
Il riquadro centrale rappresenta il formato intermedio e semi-formale
di rappresentazione dei documenti, già completamente indipendente dal
sistema logico adottato. Per la rappresentazione delle espressioni matematiche
viene utilizzato MathML content, ricorrendo pesantemente all'utilizzo di
csymbol, per esempio per rappresentare i costruttori dei termini di CIC come
Prod o Lambda. Per codificare tutte le informazioni che non sono espressioni
matematiche, è necessario ricorrere ad un secondo tipo di markup XML, che
è in corso di definizione.
Idealmente, grazie alla scelta dello standard
MathML, il formato intermedio può essere utilizzato per esportare
informazioni verso tool per la matematica non formalizzata, come, per esempio,
sistemi per il calcolo simbolico; concretamente, questo diventa impossibile
in assenza dell'associazione di una semantica ai csymbol, la quale potrebbe
essere fornita definendo opportuni content-dictionary OpenMath.
Le frecce solide che hanno come sorgente i sistemi formali e bersaglio il
formato intermedio rappresentano opportuni stylesheet XSLT, che verranno
descritti nel paragrafo 6.2. Poiché ad ogni notazione matematica
corrispondono una o più regole di trasformazione, deve necessariamente
essere previsto un meccanismo che permetta all'utente di combinare assieme
più stylesheet, uno per ogni notazione scelta, prima di applicarli al
documento in input; la soluzione adottata viene descritta nel capitolo
7.
Per associare alle espressioni semi-formali del formato intermedio quelle
formali da cui derivano si ricorre allo standard XLink:
ad ogni elemento XML che è radice di una (sotto)espressione viene aggiunto
un link alla radice della corrispondente (sotto)espressione nel file in input.
Tutti gli XLink specificano lo stesso documento, ma differiscono per
l'XPointer, ovvero la stringa che identifica l'elemento XML all'interno del
file.
Inizialmente, il formato scelto per gli XPointer è stato quello della
descrizione del cammino radice-foglia all'interno dell'albero XML; le altezze
molto elevate degli alberi DOM dei l-termini richiedevano XPointer
di lunghezze risibili, dell'ordine delle centinaia di caratteri per gli
oggetti più complessi. Pertanto, ad ogni elemento XML che possa essere
bersaglio di un XLink è stato aggiunto nel DTD riportato in appendice
A un attributo univoco id di tipo ID.
I riquadri a destra rappresentano i formati di resa per gli oggetti della
libreria, quali HTML, XML, MathML presentation o LATEX. La separazione fra
il livello degli oggetti e quello dei termini può essere completamente
ignorata oppure preservata utilizzando markup di diverso tipo.
Le frecce solide dal formato intermedio a quelli di resa rappresentano
altri stylesheet XSLT. Come per le precedenti trasformazioni, la scelta
dello stylesheet da applicare, cosí come quella del formato di output
desiderato, deve essere lasciata all'utente, grazie ai meccanismi che
descriveremo nel capitolo 7.
Infine, XLink viene utilizzato per associare alla presentazione di una
espressione la sua definizione formale, esattamente nello stesso modo e
con la stessa sintassi già utilizzati per il formato intermedio.
6.2 Gli stylesheet notazionali
Per risolvere i problemi notazionali sono stati scritti alcuni stylesheet
la cui unica finalità è la rimatematizzazione e la successiva resa
dei l-termini:
quando il termine è la codifica di un'espressione matematica per la
quale è stata specificata sotto forma di stylesheet una notazione, questa
deve essere utilizzata; negli altri casi il termine deve essere reso
senza ulteriori trasformazioni, ma adottando un'opportuna politica di
indentazione che ne massimizzi la leggibilità. Concretamente è necessario
fornire:
-
Uno o più stylesheet dal formato CIC a quello MathML content che
descrivano le
trasformazioni di default; ad ogni elemento specificato dal DTD deve
essere associata una trasformazione.
- Un meccanismo che permetta agli utenti di scrivere nuovi stylesheet
dal formato CIC a quello MathML content che descrivano le trasformazioni
particolari associate alle varie notazioni. Durante l'applicazione degli
stylesheet, se nessuna notazione particolare è applicabile ad un elemento,
allora deve essere utilizzata la trasformazione di default. È necessario
fornire un'opportuna politica per la risoluzione di eventuali
conflitti, ovvero i casi in cui ad un elemento venga associata più di una
notazione.
- Uno stylesheet per ogni formato di output che descriva la
trasformazione
dal formato intermedio a quello voluto. Tale trasformazione non è affatto
banale, in quanto è responsabile del layout del documento generato. In
altre parole, è in questa fase che è necessario decidere l'indentazione
del documento, basandosi sulle dimensioni della pagina e sulla semantica
delle formule.
Analizziamo esclusivamente le peculiarità delle soluzioni adottate. Per quanto
riguarda il punto A, sono stati scritti due stylesheet, uno per il
livello degli oggetti e uno per quello dei termini. Il primo, la cui
implementazione non ha presentato difficoltà, essenzialmente
ricopia i tag del livello content aggiungendo gli opportuni XLink al file
sorgente e richiama il secondo quando incontra i corpi e i tipi degli oggetti.
Per quanto riguarda il secondo, l'unica difficoltà è stata l'assenza in
MathML content di tutti gli elementi corrispondenti ai possibili nodi di CIC,
ad eccezione della l-astrazione e dell'applicazione. Per quanto riguarda
quest'ultima, abbiamo preferito non identificarla con quella di CIC; infatti,
l'applicazione di MathML non corrisponde all'usuale applicazione di funzione,
bensí al nodo applicazione negli alberi di sintassi astratta delle
espressioni matematiche. Per esempio, l'espressione n > 0 in MathML
content diventa
<apply>
<gt/>
<ci>n</ci>
<ci>0</ci>
</apply>
dove l'elemento apply non può essere visto come un'applicazione in quanto
l'operatore > non è una funzione, bensí una relazione.
Conseguentemente
abbiamo utilizzato un csymbol per ogni nodo CIC diverso dalla
l-astrazione, compresa l'applicazione; inoltre, sono stati utilizzati
due csymbol differenti per il prodotto dipendente e quello indipendente, che
in CIC è un caso particolare del precedente. Nell'esempio seguente viene
mostrata la regola utilizzata per l'applicazione:
<xsl:template match="APPLY" mode="noannot">
<m:apply helm:xref="{@id}">
<m:csymbol>app</m:csymbol>
<xsl:apply-templates mode="noannot" select="*"/>
</m:apply>
</xsl:template>
Si noti l'introduzione come attributo ``helm:xref'' dell'XLink che
alla radice dell'albero generato dall'elemento APPLY associa il riferimento
a quest'ultimo. Tutte le altre regole dello stylesheet sono essenzialmente
simili.
Per quanto riguarda il punto B, i meccanismi di inclusione, importazione
e controllo della priorità forniti da XSLT sono sufficienti a risolvere
il problema dei conflitti fra notazioni e quindi anche il caso particolare
del ricorso alle regole di default. Il vero problema, quindi, rimane quello
di permettere all'utente di combinare dinamicamente diversi stylesheet
ordinati per priorità crescente in quanto XSLT è, riguardo a questa
esigenza, estremamente carente: l'importazione e l'inclusione di uno stylesheet
all'interno di un altro, infatti, può essere eseguita esclusivamente
in modo statico. La soluzione consiste nella realizzazione di un programma,
integrato nell'interfaccia di accesso alla libreria, che, dato l'elenco degli
stylesheet da combinare, sintetizzi un nuovo stylesheet che includa tutti
quelli dell'elenco; resta, però, il problema di fornire all'utente l'elenco
delle notazioni applicabili, che verrà affrontato nelle fasi successive
con l'introduzione di appositi metadati.
La scrittura degli stylesheet notazionali dal livello CIC a quello content
è un'operazione resa non affatto
banale dalla possibilità di avere applicazioni parziali di funzioni, per
le quali la notazione è spesso non applicabile, e dal meccanismo di cottura
di Coq che rende difficoltosa la distinzione dell'istanzazione dei parametri
delle costanti (ingredienti) dall'applicazione di queste ad argomenti.
Per esempio, quella che segue è la regola per la notazione
``Ï'' per la non-appartenenza insiemistica:
<xsl:template match="
APPLY[
CONST[attribute::uri='cic:/coq/INIT/Logic/not.con']
and (count(child::*) = 2)
and APPLY[CONST[
attribute::uri='cic:/coq/SETS/Ensembles/Ensembles/In.con'
]]
]" mode="noannot">
<xsl:variable name="no_params">
<xsl:call-template name="get_no_params">
<xsl:with-param name="first_uri" select="/cicxml/@uri"/>
<xsl:with-param name="second_uri" select="APPLY/CONST/@uri"/>
</xsl:call-template>
</xsl:variable>
<xsl:choose>
<xsl:when test=
"(count(APPLY/child::*) - number($no_params)) = 3">
<m:apply helm:xref="{@id}">
<m:notin/>
<xsl:apply-templates select="*[2]/*[3+$no_params]"
mode="noannot"/>
<xsl:apply-templates select="*[2]/*[2+$no_params]"
mode="set"/>
</m:apply>
</xsl:when>
<xsl:otherwise>
<xsl:apply-imports/>
</xsl:otherwise>
</xsl:choose>
</xsl:template>
La regola fa match con l'applicazione (totale, due argomenti) della costante
``not'', che non ha parametri, all'applicazione della costante ``In'' ai suoi
argomenti;
la prima operazione compiuta è il calcolo del numero dei parametri
attesi in input dalla costante ``In'' al livello di cottura corrente,
determinato a partire dall'URI del file corrente (``first_uri'') e dall'URI
della costante (``second_uri''). Successivamente viene verificato se
l'applicazione della costante ``In'' è totale o meno (i due argomenti attesi
oltre agli ingredienti
sono, nell'ordine, l'insieme e l'elemento): se la risposta è affermativa si
utilizza la speciale notazione, altrimenti si richiamano le regole di default.
Poiché la scrittura degli stylesheet notazionali dal livello CIC a quello
content è complicata, ripetitiva, prona ad errori e deve essere svolta dagli
utenti che scrivono le teorie, che
tipicamente non sono conoscitori di XSLT, un interessante problema aperto è
quello della possibilità di sviluppare tool semiautomatici per generare gli
stylesheet a partire dalle definizioni degli operatori in CIC e da
descrizioni concise delle notazioni, che possono essere date in modo
testuale o tramite interfacce grafiche.
I problemi legati al punto C, quello della scrittura degli stylesheet dal
livello presentation a quello content, sono dipendenti dalla scelta del
formato di output. Limitandoci al caso della scelta di MathML presentation,
bisogna affrontare la carenza dello standard per quanto riguarda i meccanismi
di layout delle formule che non stiano nella pagina a meno di essere mandate
a capo. Poiché in HELM le prove vengono rappresentate tramite formule, è
frequente ottenere espressioni estremamente complesse e capaci di occupare anche
numerose schermate. Il fatto che usualmente le espressioni utilizzate in
matematica siano molto meno complesse giustifica solo parzialmente la scelta
di non definire meccanismi precisi nello standard: i browser per
MathML presentation non sono nemmeno obbligati a fornire un qualunque
meccanismo. Questa pratica non è affatto sorprendente e riprende la filosofia
di LATEX, in cui le formule vengono spezzate in maniera triviale, lasciando
l'onere all'utente di strutturare le formule complesse tramite l'utilizzo
di tabelle, esattamente come è possibile fare anche in MathML.
Quest'ultima soluzione, però, si presta male all'automatizzazione:
sono stati sviluppati diversi stylesheet per la conversione di MathML content
markup in MathML presentation markup, ma nessuno gestisce l'andata a capo
di formule complesse. I motivi della difficoltà di questa gestione sono
dovuti sia all'impossibilità di sapere quali saranno le dimensioni dei
bounding box di ogni sottoformula, sia alla necessità di conoscere la
semantica dell'espressione della quale si vuole fare il layout per poter
decidere in quali punti spezzarla e quali indentazioni applicare.
Pertanto, è stato necessario scrivere uno stylesheet
di conversione da MathML content a MathML presentation che gestisca il layout
di formule estese e consideri anche i csymbol utilizzati in HELM a livello
content. Lo stylesheet procede a grandi linee in questo modo: ogni volta
che un elemento fa match con una regola, viene stimata la larghezza della
sua rappresentazione e questa viene sottratta alla larghezza residua prima
di terminare la pagina; se il valore ottenuto è positivo la formula
non viene spezzata e le si applica la trasformazione canonica; altrimenti
viene creata una tabella in cui vengono inserite, con un'opportuna indentazione
e procedendo per ricorsione, le rappresentazioni delle sottoformule, calcolate
sottraendo alla larghezza residua della pagina l'indentazione applicata.
Come regole canoniche vengono utilizzate quelle di uno stylesheet scritto
da Igor Rodoniov del Computer Science Department della University of
Western Ontario, London, Canada: un ottimo esempio di riutilizzo del codice
reso possibile dall'adozione degli standard XSLT e MathML.
6.3 Alcune idee per la resa delle prove
Come già anticipato a pagina 8, non esistono
ancora soluzioni
soddisfacenti al problema della difficile comprensibilità delle dimostrazioni
scritte in un sistema formale, anche se è ormai chiaro che l'obiettivo
richiede di fornire almeno una descrizione (iper)testuale in linguaggio
naturale della prova, simile a quelle normalmente presenti nei testi cartacei.
Il valore aggiunto dalle librerie elettroniche rispetto a questi ultimi, oltre
che nella facilità di reperimento delle informazioni, consiste
nell'ipertestualità del documento e nella possibilità di avere diversi
livelli di dettaglio per le prove, da quello iperdettagliato del termine
formale a quello altamente non informativo dell'omissione della prova
(``Dimostrazione: ovvia''). Inoltre, personalmente ritengo che un ulteriore
valore aggiunto consista nella possibilità, da parte dell'utente, di poter
``annotare'' la descrizione con propri commenti, esattamente come
normalmente avviene nel mondo cartaceo, ma con una potenza espressiva molto
maggiore data dall'ipertestualità.
Fino ad ora i soli approcci in corso di sperimentazione sono quelli della
sintesi automatica della descrizione naturale a partire o dalla prova formale
o dalla sequenza di tattiche applicate1.
Come già mostrato a pagina 2.3.2, tale approccio è
insoddisfacente, ma il risultato ottenuto è un'ottima base di partenza per
una successiva (ri)annotazione della prova. Per questo motivo, nell'ambito
del progetto HELM è in corso di scrittura un sistema di stylesheet per
la generazione automatica della descrizione in linguaggio pseudo-naturale
delle prove. Nel paragrafo 6.3.2 vengono descritte le
problematiche
che si dovranno affrontare seguendo questo approccio; nel prossimo paragrafo,
invece, viene proposta una nuova soluzione alternativa.
6.3.1 Le annotazioni
A mio avviso, un modo per superare i limiti dell'approccio basato sulla
sintesi automatizzata consiste
nell'utilizzo di annotazioni strutturate intese non solo come
note e commenti aggiunti alla descrizione, ma viste come la descrizione stessa
in linguaggio naturale dei termini. Concretamente, la mia proposta consiste
nella possibilità di associare ad ogni nodo di un termine CIC una annotazione
scritta in XML. Il contenuto dell'annotazione consiste di due tipi di markup
distinti, quello di output per la descrizione di testo e formule matematiche
e quello di ricorsione i cui elementi sono riferimenti agli attributi del nodo
corrente, riferimenti ad altri nodi o uno speciale elemento che indica la
descrizione formale del nodo corrente. Per effettuare la resa delle prove
è necessario
fornire un nuovo stylesheet che compia ``ricorsivamente'' la seguente
operazione a partire dalla radice dell'albero:
-
Se il nodo corrente è privo di annotazione, richiama la regola
opportuna dello stylesheet per i termini non annotati, ovvero quello per
la resa del l-termine.
- Altrimenti itera su ogni elemento dell'annotazione in questo modo:
-
Se incontri un elemento del markup di output, ricopialo.
- Se incontri un riferimento ad un attributo del nodo corrente, stampa
il valore dell'attributo.
- Se incontri l'elemento che indica la descrizione formale del nodo
corrente, richiama la regola opportuna dello stylesheet per i termini
non annotati.
- Se incontri un riferimento ad un altro nodo, processa con la regola
più esterna il nodo puntato.
Si osservi che, se l'annotazione di un nodo non contiene riferimenti ad
altri nodi, al termine della stampa del markup di output la funzione
termina. Quindi, per esempio, se il nodo radice ha come annotazione
esclusivamente il markup di output contenente la stringa ``Ovvio'',
allora la resa complessiva del termine sarà tale stringa e tutti gli
altri nodi dell'albero non saranno visitati.
Nonostante l'algoritmo sia già stato interamente specificato, il formato
dei riferimenti è ancora imprecisato e determina il grado di fedeltà
della descrizione in linguaggio naturale al l-termine. In particolare,
se tutti i possibili riferimenti sono ammessi, allora la resa del termine
può avvenire distruggendo la struttura del termine e visitandone i nodi
in un qualsiasi ordine. Al contrario, se ogni nodo può riferire
esclusivamente i propri figli, l'albero delle annotazioni non può essere
che isomorfo ad un sottoalbero di quello del termine, a meno dell'ordine
relativo fra i figli di uno stesso nodo e con il vincolo aggiuntivo che
le due radici siano in relazione fra loro. Nonostante la seconda soluzione
sembri decisamente più attraente, i primi esperimenti compiuti indicano
che la resa migliore si ottiene utilizzando vincoli intermedi, che permettano
esclusivamente alcune riorganizzazioni dell'albero di partenza: per esempio,
è una buona scelta anticipare la descrizione degli argomenti di una
applicazione prima dell'applicazione stessa quando questi siano prove non
atomiche di proposizioni e la funzione applicata sia la prova di una
implicazione, come nel caso seguente:
Siano transXYZ e transX0Y due istanze della prova della proprietà
transitiva della relazione ``>'', rispettivamente di tipo
(X>Y) ® (Y>Z) ® (X>Z) e
(X>0) ® (0>Y) ® (X>Y),
e siano
P una prova di (X>0), N una prova di (0>Y) e H una prova di (Y>Z).
La dimostrazione (transXYZ (transX0Y P N) H) della tesi (X>Z)
viene normalmente resa come:
``Per la proprietà transitiva transX0Y applicata alle ipotesi P e
N si ha X>Y. Da qui, per la proprietà transitiva transXYZ e
l'ipotesi H, si ha la tesi.''
La precedente descrizione viene facilmente ottenuta ricorrendo alle seguenti
annotazioni:
-
Applicazione più esterna:
-
``<<riferimento all'applicazione più interna>>
Da qui, per la proprietà transitiva
<<riferimento al primo figlio della funzione>> e
l'ipotesi
<<riferimento al terzo figlio della funzione>>, si
ha la tesi.''
- Applicazione più interna:
-
``Per la proprietà transitiva
<<riferimento al primo figlio della funzione>> applicata
alle ipotesi
<<riferimento al secondo figlio della funzione>> e
<<riferimento al terzo figlio della funzione>> si ha
X>Y.
La soluzione basata sulle annotazioni è suscettibile di due critiche:
-
Non vi è alcuna garanzia che l'annotazione di un nodo corrisponda
alla descrizione informale e corretta del nodo stesso.
- Poiché annotare un termine è tanto difficile quanto capire la
prova formale, annotare termini di grosse dimensioni è impraticabile.
Pur essendo la prima critica sicuramente valida, l'unica garanzia
sulla corrispondenza fra la descrizione informale e quella formale verrebbe
dalla generazione automatica della prima a partire dalla seconda, procedura
che è insoddisfacente, almeno rispetto all'attuale stato dell'arte.
Pertanto, l'idea di utilizzare le annotazioni è giustificata dal seguente
compromesso:
la provabilità dei teoremi annotati non è messa in discussione, in quanto
è sempre possibile richiamare un proof-checker sul sottostante termine
formale, mentre la garanzia della correttezza della prova che viene letta
è sacrificata alla sua leggibilità. Si noti che, in ogni caso, il
vantaggio rispetto alle prove cartacee è notevole: innanzi tutto per queste
non viene garantita nemmeno la provabilità della tesi; inoltre, nel caso
che venga trovato un errore in una prova, nel caso cartaceo è necessario
cercare una nuova prova ripartendo da zero, mentre nel caso delle annotazioni
è sufficiente deannotare il (sotto)termine male annotato e riannotarlo con
la descrizione corretta (che esiste sempre!) del termine formale sottostante.
Il problema messo in luce dalla seconda critica è reale, ma può essere
affrontato in molteplici modi. Innanzi tutto, come abbiamo potuto sperimentare
realizzando un piccolo prototipo di un'interfaccia grafica per l'ausilio
all'annotazione, una buona interfaccia, che permetta di selezionare
interattivamente il sottotermine da annotare e che metta a disposizione una
palette con gli elementi del markup di ricorsione, è sufficiente a rendere
agevole un'operazione altrimenti complessa e prona ad errori. Inoltre,
è possibile ripensare ai tool per la generazione automatica delle descrizioni
in linguaggio formale delle prove come a dei tool per la generazione automatica
delle annotazioni. In questa ottica, il problema di innaturalezza dei prodotti
di questi tool scompare grazie alla possibilità di riannotare manualmente
le descrizioni seguendo la traccia proposta e intervenendo esclusivamente
sulle parti troppo prolisse, troppo artificiali o poco intuitive.
Infine, è ragionevole pensare
che sia possibile scrivere proof-assistant che, ad ogni passo della
dimostrazione, ovvero ad ogni applicazione di una tattica, permettano
all'utente di inserire la descrizione informale del ragionamento effettuato,
salvandola come annotazione del nodo radice del termine generato dalla
tattica2. Il principale vantaggio di questa ultima soluzione consisterebbe
nell'esatta corrispondenza fra l'annotazione e il ragionamento effettuato
e l'eliminazione del problema della comprensione del termine formale per
poterlo riannotare; d'altro canto, la corrispondenza che si instaurerebbe fra
l'uso di una tattica e la scrittura dell'annotazione costringerebbe a
presentare le prove nella stessa maniera con cui vengono cercate, ovvero
quella top-down, mentre diversi secoli di pratica matematica ci hanno insegnato
che il modo migliore di presentare le dimostrazioni è tipicamente quello
bottom-up.
6.3.2 La generazione automatica delle annotazioni.
In questo paragrafo vengono rapidamente presentati i problemi che si incontrano
cercando di realizzare tramite stylesheet XSLT un generatore automatico di
descrizioni in linguaggio naturale a partire dai l-termini della
libreria di HELM3. In quello che segue, si
assumerà che il prodotto della trasformazione sia un'annotazione, nel senso
del precedente paragrafo; pertanto, si può immaginare che lo stylesheet venga
comunque applicato off-line, potendo quindi essere computazionalmente costoso,
e inoltre che non venga richiesto un output particolarmente raffinato grazie
alla possibilità di riannotare la descrizione.
Il principale problema da affrontare è la mancanza nel l-termine
di parte dell'informazione necessaria per una buona resa, ovvero quella
relativa ai tipi e talvolta alle sort di alcuni sottotermini, come si può
vedere nell'esempio precedente a pagina 111:
la formula X>Y inserita manualmente nell'annotazione dell'applicazione
più interna corrisponde al tipo, non disponibile, di tale applicazione
; il problema si presenta ogni volta che bisogna
effettuare la resa di termini contenenti nodi applicazione di sort
Prop.
Un secondo esempio in cui sarebbe necessario conoscere la sort di un termine
è quello della resa dei prodotti dipendenti: se la sort del prodotto è
Prop, allora la sua resa appropriata è come quantificatore
universale.
Nonostante le precedenti informazioni mancanti siano sintetizzabili a partire
dal l-termine ricorrendo alla type-inference, tale operazione è troppo
onerosa da compiere in uno stylesheet, sia dal punto di vista della
complessità implementativa che da quello puramente prestazionale: un
primo prototipo incompleto per CIC, ottenuto reimplementando in XSLT
parte del codice OCaml del proof-checker, ha richiesto circa 1100 linee
di codice e richiede diversi minuti per la sintesi dei tipi mancanti in
l-termini di piccole dimensioni. La soluzione più semplice
consisterebbe nell'aggiungere ai file XML tali tipi direttamente in fase
di esportazione, contravvenendo pesantemente al principio di minimalismo
e diminuendo le prestazione del proof-checker. Una soluzione simile, ma
esente dai precedenti problemi, consiste nell'esportare tali tipi in un
secondo file, che deve essere già considerato un file di annotazioni;
pertanto, nessuna garanzia viene fornita sul suo contenuto, che non viene
cosí esaminato dal proof-checker. Infine, una terza soluzione consiste
nel far richiamare allo stylesheet un motore di type-inference esterno,
implementato in un qualunque linguaggio. Tale soluzione potrebbe risultare
la migliore, ma non esiste purtroppo alcuno standard per permettere ad
uno stylesheet di invocare un programma esterno4.
Un altro importante problema, che dovrà essere affrontato e che è
un'istanza di quello più generale che si avrà con qualsiasi tipo di
annotazione, consiste nell'individuazione del livello, content o
presentation, al quale sostituire le annotazioni ai termini formali.
Attualmente, entrambe le soluzioni possibili non sono soddisfacenti:
utilizzare le annotazioni solamente al livello presentation costringe
ad avere più di una annotazione per ogni file, una per ogni possibile
formato di output, e in questo modo verrebbe calcolata la rappresentazione
a livello content di termini che non saranno successivamente mostrati a
livello presentation. Inoltre, dal momento
che la prima fase di trasformazioni corrisponde concettualmente alla
rimatematizzazione del documento, sembrerebbe più corretto applicare
a livello content le annotazioni, che rappresentano una possibile
rimatematizzazione informale delle prove. Questa soluzione, però,
costringerebbe ad utilizzare come markup di output per le annotazioni
un linguaggio di descrizione del documento compilabile in ogni possibile
formato di output, ovviamente non permettendo di sfruttare le potenzialità
di questi. Inoltre, in questo modo, elementi del content markup di MathML
potrebbero avere come figli elementi del markup di output, contravvenendo
alle specifiche di MathML: infatti, affinché il content markup
possa essere utilizzato per lo scambio di dati fra applicazioni che utilizzano
MathML, è necessario che la semantica delle espressioni
scambiate sia univoca, almeno in assenza di csymbol; questa proprietà
non sarebbe ovviamente rispettabile utilizzando all'interno del termine markup
estraneo, privo di semantica.
Ora, alla luce delle precedenti osservazioni, non è possibile escludere
un ridisegno dell'architettura complessiva delle trasformazioni XSLT, con
l'aggiunta di eventuali livelli intermedi fra quello content e quello
presentation. Nel frattempo, però, si è notata la possibilità di
fattorizzare la trasformazione compiuta dal generatore automatico di
annotazioni in due fasi: la prima prevede la riorganizzazione della struttura
dell'albero di prova, per esempio al fine di anticipare le prove dei risultati
parziali, ed è legata al markup di ricorsione; la seconda sostituisce i
termini formali con il markup di output. Mentre non è ancora chiaro se
e come queste due fasi possano corrispondere al livello content e a quello
presentation, è immediato notare che il primo tipo di trasformazione
non altera il contenuto informativo delle prove e può essere internalizzata
nel sistema logico a cui venga aggiunto un operatore di naming, usualmente
chiamato ``let ... in'': alla produzione sintattica
per i termini di CIC viene aggiunto il costrutto
let r = t1 in t2 dove r è un identificatore e
t1 e t2 sono termini; let r = t1 in t2 è ben
tipato quando t2[t1/r] è tale e in questo caso ha lo stesso tipo; infine
viene introdotta un nuovo tipo di conversione =let, simile
all'a-conversione e chiamata let-conversione,
definita da (let r = t1 in t2) =let t2[t1/r].
In questo modo l'operazione di riorganizzazione dell'albero di prova
corrisponderebbe semplicemente alla sua sostituzione con un altro albero ad esso
let-convertibile.
La precedente osservazione è particolarmente interessante in quanto
l'operatore di naming, nonostante sia logicamente irrilevante5, può
contribuire pesantemente all'aumento della leggibilità delle dimostrazioni
e può essere utilizzato per diminuire notevolmente le dimensioni dei
l-termini in cui uno stesso sottotermine compaia più volte.
In particolare, quest'ultima proprietà e la frequenza della sua
applicabilità hanno spinto il team di Coq
ad aggiungere l'operatore a CIC nella nuova versione del proof-assistant
attualmente in sviluppo.
Infine, come per le trasformazioni notazionali, il meccanismo di generazione
automatica dovrà essere estendibile per permettere agli utenti di associare
ai principi di eliminazione dei nuovi tipi (co)induttivi un'opportuna
descrizione in linguaggio naturale. Per esempio, l'applicazione del principio
di eliminazione sui numeri naturali potrà essere trasformata nella locuzione
``Procediamo per induzione su .... Caso base: ...Passo induttivo: ...'', mentre quello di eliminazione del tipo induttivo
``or'' potrà diventare ``Procediamo per casi. Se è vero ...allora ...altrimenti ...''.
6.4 Risultati ottenuti.
Dai membri del progetto HELM sono già stati sviluppati numerosi stylesheet
notazionali, dei quali riportiamo a titolo indicativo le dimensioni in
numero di linee di codice e numero di file in cui queste vengono strutturate:
| CIC ® content |
| Trasformazioni di default dal livello CIC a quello content, comprendenti
anche il livello dei termini |
7 stylesheet, 819 linee |
| Trasformazioni dal livello CIC a quello content per le notazioni relative
alle operazioni insiemistiche, logiche e sui numeri reali |
3 stylesheet, 1017 linee |
|
| content ® presentation |
| Trasformazioni con output MathML presentation dal livello content a
quello presentation dei soli elementi prodotti dai precedenti stylesheet;
sono escluse le trasformazioni canoniche |
3 stylesheet, 1052 linee |
| Trasformazioni con output HTML dal livello content a quello presentation
dei soli elementi prodotti dalle trasformazioni di default dal livello
CIC a quello content |
1 stylesheet, 657 linee |
| Trasformazioni con output HTML dal livello content a quello presentation
dei soli elementi prodotti dalle trasformazioni per le notazioni relative
alle operazioni insiemistiche, quelle logiche e quelle sui numeri reali |
3 stylesheet, 956 linee |
|
Riportiamo, inoltre, le dimensioni dello stylesheet scritto da Igor Rodoniov
e richiamato dalle trasformazioni di default dal livello content a quello
presentation:
| Trasformazioni canoniche da MathML content a MathML presentation |
1 stylesheet, 1848 linee |
Per quanto riguarda la resa delle prove, non si hanno ancora risultati
definitivi, ma si sta lavorando sia sul fronte
dell'annotazione manuale, costruendo un'interfaccia prototipo, sia su quello
della generazione automatica, scrivendo opportuni stylesheet. L'interfaccia,
ancora decisamente grezza per quel che riguarda l'ausilio all'annotazione,
viene descritta nel paragrafo 7.2. Descriviamo ora brevemente la
soluzione adottata per la generazione automatica.
Il primo problema affrontato è stato quello della sintesi
dei tipi mancanti. Come esperimento, è stato scritto dal Prof. Asperti
uno stylesheet, ancora ampiamente incompleto, che effettua la sintesi e produce
in output un file XML contenente la lista dei tipi sintetizzati con il
riferimento all'elemento XML del nodo CIC a cui il tipo si riferisce. Come era
lecito attendersi dal fatto che, mediamente, circa la metà dei nodi di
un l-termine sono applicazioni il cui tipo deve essere sintetizzato,
l'applicazione dello stylesheet a termini di medie dimensioni
richiede diversi minuti e genera file le cui dimensioni sono le stesse o di
poco inferiori rispetto a quelle del file sorgente.
Conseguentemente, visti gli alti tempi di elaborazione
e le dimensioni tollerabili dei file generati e considerato che l'immutabilità
dei file XML comporta l'immutabilità dei file sintetizzati, si è deciso di
effettuare la sintesi dei tipi in maniera off-line, subito dopo l'esportazione
da Coq. Inoltre, viste le scarse prestazioni della sintesi in XSLT e poiché
non vi è alcun motivo che la faccia preferire a quella scritta in un altro
linguaggio, questa verrà probabilmente rimpiazzata o affiancata da un'analoga
implementazione in OCaml.
Il secondo problema consiste nella scrittura dei due stylesheet, uno dal livello
CIC a quello content e l'altro da questo a quello presentation, che utilizzino
i tipi sintetizzati per generare la resa in linguaggio naturale del termine.
Si noti che, per il momento, l'output del processo non è un'annotazione come
ipotizzato nel paragrafo 6.3.2, ma è già la resa definitiva.
Affinché
lo stylesheet possa processare contemporaneamente due file XML, è necessario
applicarlo ad uno dei due e utilizzare la funzione XSLT ``document'' che
permette di caricare un secondo file e ne restituisce il nodo radice. A causa
di una limitazione dello standard XSLT 1.0, che verrà eliminata nella
versione 1.1, non è possibile invocare la funzione
``document'' una volta sola, memorizzandone il risultato in una variabile per
poterlo riutilizzare successivamente, costringendo a ripetute
invocazioni6. In teoria, tali
invocazioni ripetute non dovrebbero essere computazionalmente costose, in quanto
lo standard prescrive che due invocazioni distinte della funzione ``document''
aventi come parametro lo stesso URI ritornino la stessa copia del documento
scaricato. In realtà, tutte le implementazioni disponibili, uniformandosi
alle regole per il caching utilizzate nei browser HTML, riscaricano il documento
ogni volta nel caso che l'URI sia un URL che punti ad un contenuto dinamico,
ovvero, per esempio, contenente passaggio di parametri secondo il metodo HTTP
post. Questa caratteristica, nonostante non sia conforme allo standard, è
estremamente utile in quanto consente di utilizzare lo stratagemma descritto
nella nota 4 a pagina 114.
Nel caso di HELM, tutti i
documenti vengono richiesti al getter con interfaccia HTTP e sono quindi
riconosciuti come dinamici; come conseguenza, non è possibile per motivi
prestazionali invocare ripetutamente la funzione ``document''. Invece di
ricorrere all'estensione proprietaria del processore XSLT per trasformare
i result tree fragment in node set, abbiamo preferito aggiungere
all'implementazione del getter con interfaccia HTTP la quarta funzionalità
opzionale descritta a pagina 74, ovvero la possibilità di
effettuare sintesi di documenti XML a partire da fonti distinte. Concretamente,
è stato aggiunto al getter un nuovo metodo che, ricevuti in input gli URI
di un oggetto CIC e del file contenente i relativi tipi sintetizzati, costruisce
un nuovo documento XML ottenuto creando un nuovo nodo radice avente come figli
le radici dei due documenti.
Non descriveremo in questo lavoro gli algoritmi implementati nei due stylesheet
in quanto questi non sono ancora terminati e saranno presto sottoposti ad una
riorganizzazione complessiva.
Concludendo, nonostante, una volta introdotta la generazione automatica delle
descrizioni in linguaggio naturale, i risultati visivi ottenuti siano
soddisfacenti, deve essere svolto ancora molto lavoro per rendere
l'architettura complessiva degli stylesheet pulita ed estendibile.
- 1
- Si vedano rispettivamente
il modulo Natural di Coq [CKT95] e quello Proverb di Omega
[Hor99].
- 2
- L'operazione non è semplice come può sembrare a prima
vista in quanto esistono tattiche che compiono trasformazioni complesse
sul l-termine. Inoltre, l'implementazione più semplice di una tattica
non si preoccupa mai della verifica che il termine generato sia il più
naturale possibile, prediligendo la facilità implementativa, ma generando
termini ingiustificatamente complessi, che vengono talvolta successivamente
semplificati, per esempio procedendo all'eliminazione di alcuni dei tagli
introdotti.
- 3
- Le osservazioni derivano in larga parte dallo
studio del Prof. Asperti che, nell'ambito del progetto HELM, sta realizzando
un primo prototipo di generatore automatico.
- 4
- Lo
standard XSLT 1.0
prevede l'implementazione di funzioni di estensione, ma non specifica alcuno
standard per l'interfacciamento di tali funzioni con il processore XSLT. Lo
standard XSLT 1.1 affronterà il problema, ma non sarà disponibile che fra
diversi mesi. Ciò nonostante, esiste già ora un modo non ufficiale, ma
funzionante con ogni processore, per ottenere un risultato analogo:
la scrittura della funzione come metodo di un HTTP server o come CGI.
Il getter descritto nel paragrafo 4.1.2 utilizza esattamente tale
stratagemma.
- 5
- Nella
particolare formulazione proposta.
- 6
- Più dettagliatamente, le variabili possono memorizzare
result tree fragment (rtf), ovvero alberi XML come quelli restituiti
dall'applicazione dell'istruzione ``value-of'' ad un XPath contenente
l'invocazione della funzione ``document''; quello che non si può fare è
applicare funzioni XPath agli rtf, impedendo quindi la selezione di nodi
dell'albero memorizzato nell'rtf. Nella prossima versione dello standard
quest'ultima limitazione verrà semplicemente eliminata; attualmente,
comunque, tutti i processori XSLT implementano come estensione proprietaria una
funzione che trasforma un rtf in un node set, sul quale è possibile applicare
funzioni XPath. Per poter scrivere lo stylesheet per la sintesi automatica,
più dettagliatamente per poter implementare la funzione di sostituzione, è
stato necessario ricorrere ad una di tali estensioni.
Chapter 7 Le interfacce utente
L'ultimo tema già in parte affrontato nell'ambito del progetto HELM
è quello dello sviluppo di interfacce responsabili di fornire un
accesso uniforme ai moduli software che operino sul formato XML (si
faccia riferimento alla figura 1.1 a pagina
14).
In conformità al terzo requisito di HELM (pagina 13),
sono state fornite due differenti interfacce: la prima permette l'accesso
alle funzionalità della libreria tramite un comune browser ed è costituita
dai siti di presentazione; la seconda è un'applicazione Gtk che è stata
estesa per trasformarla in un prototipo per il browsing e la (ri)annotazione
dei file della libreria.
7.1 I siti di presentazione
Per massimizzare la facilità di accesso ai documenti della libreria, è
necessario effettuare tutta l'elaborazione sul lato server, permettendo agli
utenti di utilizzare comuni browser come client. Al fine di non violare
l'analogo requisito di HELM volto a massimizzare la facilità di pubblicazione,
si richiede che tali server siano distinti da quelli di distribuzione.
Questo porta alla nascita dei siti di presentazione, server HTTP
che vengono contattati dagli utenti per effettuare le elaborazioni, come
il proof-checking o l'applicazione di trasformazioni XSLT, e che a loro
volta contattano i server di distribuzione per ottenere i necessari documenti
XML.
Il prototipo di sito di presentazione che abbiamo sviluppato si basa su
Cocoon, un framework per l'editoria Web basata su XML. Cocoon, che è
un software free sviluppato nell'ambito dell'Apache XML
Project1, è un servlet Java che
viene invocato dall'HTTP server ogni qualvolta viene richiesto un documento
XML. L'elaborazione dei documenti effettuata da Cocoon si basa sul modello
a pipeline, in cui il documento, sotto forma di albero DOM, viene generato da
un processo sorgente, viene trasformato da una catena di processori e infine
viene consumato da un processo pozzo. Usualmente, ma non necessariamente, il
processo sorgente è un parser XML che, dato un file XML, ne ritorna l'albero
DOM; il processo pozzo, invece, è un formatter che trasforma l'albero DOM
nella rappresentazione testuale che verrà restituita dal Web server e che,
normalmente, è un documento XML. Fra i possibili processori, quelli più
utilizzati sono i processori XSLT, anche se ne esistono numerosi altri che,
in genere, riconoscono esclusivamente gli elementi appartenenti ad un
determinato namespace e li espandono in opportuni frammenti di alberi DOM,
lasciando
inalterata la restante struttura del documento. Un processore di questo genere
è quello XSP (eXtensible Server Pages), che permette di aggiungere
all'interno del
documento elementi contenenti codice Java che verranno sostituiti dall'output
della loro esecuzione. Per motivi di efficienza, la rappresentazione dei
documenti nella pipeline, oltre che come albero DOM, può anche essere uno
stream di eventi SAX oppure una struttura proprietaria, chiamata DTM, che
è la più efficiente.
Ovviamente, è necessario un meccanismo per permettere a Cocoon di determinare
la forma della pipeline da applicare ad un documento, ovvero l'esatta sequenza
di processori da assemblare. Nelle prime versioni di Cocoon, indicate come
1.x, tale sequenza è indicata direttamente all'interno dei singoli documenti
XML, per mezzo di processing instruction XML. Il problema di questo approccio
è la mancata separazione fra contenuto ed elaborazione, reminescenza della
mancata separazione fra contenuto e presentazione in HTML, superata dagli
standard XML e XSLT. Nelle prossime versioni di Cocoon, ancora in via di
sviluppo e complessivamente indicate come Cocoon 2, questo meccanismo verrà
abbandonato e sostituito dalla site map, ovvero un file di configurazione che
descriverà la funzione che ad ogni file XML fornito dal server associa
la catena di processori da applicare.
Venendo al progetto HELM, un sito di presentazione deve essenzialmente fornire
all'utente la possibilità di indicare non solo l'URI del file XML a cui è
interessato, ma anche l'URI dell'eventuale annotazione da utilizzare,
il formato di output richiesto e la lista delle notazioni da applicare.
Poiché, come nel caso del file contenente i tipi sintetizzati, ogni file
di annotazione si riferisce ad uno e un solo file XML, nel caso in cui
si specifichi una annotazione non è più necessario fornire l'URI del
file XML. Inoltre, per gli stessi motivi esposti a pagina
118 per il
caso particolare della sintesi delle prove in linguaggio naturale, è
conveniente estendere le funzionalità del getter con interfaccia HTTP
in modo che esponga un metodo che, dato un URI, se questo si riferisce ad
una annotazione, allora viene restituito il documento sintetizzato a partire
dall'annotazione e dal file a cui questa si riferisce, mentre se si riferisce
ad un documento CIC, questo diventa l'output dell'esecuzione.
Vista l'osservazione precedente e poiché ad ogni coppia notazione--formato
corrispondono due stylesheet XSLT, uno per la trasformazione dal livello
del sistema logico a quello content e un altro per quella dal livello content
a quello presentation, è sufficiente permettere all'utente di specificare,
possibilmente in modo user-friendly,
-
l'URI dell'annotazione o del file a livello del sistema logico;
- una lista di URI di stylesheet che complessivamente descrivano la
trasformazione dal livello del sistema logico a quello content;
- una lista di URI di stylesheet che complessivamente descrivano la
trasformazione dal livello content a quello presentation.
Per evitare all'utente di doversi memorizzare gli URI degli stylesheet,
l'interfaccia più semplice consiste, una volta che sia stato indicato
l'URI del documento (o quello di una sua annotazione), nel fornire
la lista degli stylesheet applicabili e la possibilità di indicare, per
ognuno, se lo si voglia utilizzare o meno. Il problema si riduce, quindi,
a quello di conoscere quali siano gli URI degli stylesheet, ovvero delle
notazioni, rilevanti per un determinato documento. Poiché tale informazione
è un tipico esempio di metadato e la gestione dei metadati non è stata
ancora sviluppata, la costruzione di un'interfaccia user-friendly è stata
momentaneamente sospesa.
Una volta specificati gli URI da utilizzare, resta il problema della sintesi,
a partire dagli stylesheet indicati, dei due stylesheet da utilizzare
rispettivamente nella trasformazione dal livello del sistema logico a quello
content e da questo a quello presentation.
Infatti, le singole notazioni non possono essere applicate
sequenzialmente, ma solo contemporaneamente in quanto ognuna si attende come
input il formato legato al sistema formale e restituisce come output il
formato del livello content, impedendo cosí una loro serializzazione.
Anche se il
problema della serializzazione può essere risolto modificando l'architettura
degli stylesheet, l'applicazione a cascata delle notazioni non è preferibile
in quanto risulterebbe estremamente più costosa di quella parallela, che
raggiunge già tempi di elaborazione spesso inaccettabili. Per combinare le
notazioni in un unico stylesheet, è sufficiente creare un nuovo foglio di
stile XSLT che importi quelli specificati; tale operazione è facilmente
implementabile ricorrendo ad un CGI o ad una pagina XSP.
Infine, è necessario associare al documento XML scelto dall'utente la
pipeline costituita, oltre che dal processo sorgente, dai due stylesheet
sintetizzati come descritto in precedenza e dal processo formatter
corrispondente al formato di output indicato dall'utente, per esempio
HTML o XML. La soluzione adottata, in attesa dell'uscita di Cocoon 2,
consiste in una pagina XSP (un processo sorgente) che, dati i tre URI
necessari, produca in output l'albero DOM, ottenuto effettuando il parsing
del documento matematico, a cui vengono aggiunti tre processing instruction
indicanti rispettivamente l'URI del primo e del secondo stylesheet da
applicare per mezzo di un processore XSLT e il formatter scelto (processo
pozzo).
7.1.1 Risultati ottenuti
Nonostante il prototipo fornito sia già perfettamente funzionante, restano
due problemi che ne precludono seriamente l'utilizzo:
-
La mancanza di browser in grado di riconoscere il formato MathML
- Gli elevati tempi di elaborazione
Il primo problema è solo temporaneo in quanto le principali case produttrici
di browser stanno aggiungendo il supporto per MathML ai loro prodotti, anche
se lo sviluppo procede molto lentamente a causa dello scarso interesse
commerciale dovuto al basso numero di potenziali utilizzatori di MathML.
Per ovviare parzialmente al problema, è stato realizzato dal Dott. Luca
Padovani nell'ambito del progetto HELM un widget Gtk realizzato in C++, chiamato
MathView, per la resa delle espressioni MathML presentation che compaiano
all'interno di documenti XML. Il widget, del quale è stata rilasciata la prima
versione stabile, riconosce tutti gli elementi e gli attributi di presentation
markup descritti dalla specifica, a cui è pienamente conforme (ad eccezione
dei due valori ``leftoverlap'' e ``rightoverlap'' dell'attributo ``side''
dell'elemento ``mtable'' che non vengono riconosciuti),
ed è la prima implementazione che gestisce automaticamente il layout di
formule di arbitraria grandezza;
inoltre, ha un meccanismo che permette la selezione esclusivamente
di alcune sottoformule, determinate dalla presenza di un attributo opzionale
sul nodo radice.
Il secondo problema non è di facile soluzione ed è una diretta conseguenza
delle scarse prestazioni degli attuali processori XSLT, tutti scritti in
linguaggio Java. Nel giro di pochi mesi si attende l'uscita di una nuova
generazione di processori, scritti in differenti linguaggi e con un
particolare riguardo per le prestazioni, che dovrebbero alleviare il problema:
il prototipo più avanzato di processore XSLT scritto in C++,
Xalan-C2, è circa un ordine di
grandezza più veloce della corrispondente implementazione in Java. Tale
incremento di prestazioni, comunque, nonostante renderebbe accettabili i
tempi di elaborazione per i documenti più semplici, non sarebbe ancora
sufficiente per quelli più complessi, che oggi richiedono tempi superiori
ai dieci minuti.
7.2 L'interfaccia sviluppata in Gtk
La creazione di siti di presentazione permette di usufruire della libreria
di HELM senza la necessità di installare sulla macchina dell'utente alcun
tipo di software, ma non permette di contribuire alla libreria, per esempio
annotandone alcuni degli oggetti o esportando nuove teorie: tali operazioni,
per motivi essenzialmente prestazionali, debbono essere svolte sul lato client.
Pertanto, è stata sviluppata un'interfaccia grafica in Gtk,
l'emergente standard per la realizzazione di interfacce grafiche in ambiente
Unix, scritta in OCaml. Successivamente, l'interfaccia è stata estesa,
trasformandola in un prototipo di interfaccia per la (ri)annotazione delle
prove; le funzionalità attualmente messe a disposizione sono:
-
Visualizzazione di un menu ad albero in cui sono riportati tutti gli
oggetti e le teorie a conoscenza del getter.
- Visualizzazione degli oggetti o delle teorie in formato MathML
presentation, ottenuto applicando agli oggetti le trasformazioni descritte nel
precedente capitolo3.
- Possibilità di invocare il proof-checker sull'oggetto o la teoria
attualmente visualizzati.
- Navigazione ipertestuale ottenuta tramite hyperlink che
associano alle occorrenze dei nomi degli oggetti le loro
definizioni4.
- Possibilità di selezionare esclusivamente le espressioni che
corrispondono alla presentazione di un nodo CIC annotabile.
- Possibilità di (ri)annotare il nodo selezionato scrivendo manualmente il
markup che costituisce l'annotazione. Per l'introduzione degli elementi di
ricorsione e di quelli che selezionano gli attributi del nodo corrente,
l'interfaccia propone anche una palette dei suggerimenti: ogni pulsante della
palette, quando premuto, inserisce nella posizione corrente dell'annotazione il
markup corrispondente al suggerimento.
Nel prossimo paragrafo verranno descritte le principali scelte progettuali.
La descrizione dell'implementazione viene, invece, omessa in quanto non ha
presentato particolari difficoltà.
7.2.1 Progettazione
Lo sviluppo del prototipo è stato articolato in due fasi distinte: nella
prima è stata sviluppata l'interfaccia Gtk nella quale sono stati integrati
il proof-checker sviluppato nel capitolo 5,
un processore XSLT e, come
browser per MathML presentation, il widget MathView; nella seconda fase è
stato aggiunto il supporto per la (ri)annotazione.
Prima fase
Le scelte progettuali preliminari alla progettazione della prima fase sono
state:
-
L'interfaccia deve basarsi sull'emergente standard Gtk per
sfruttarne le caratteristiche di portabilità. La libreria Gtk, infatti,
è oggi disponibile per diverse architetture e sotto diversi sistemi
operativi; inoltre, esistono binding per Gtk per tutti i linguaggi di
programmazione più diffusi, compreso OCaml.
- Deve essere possibile con poco sforzo implementativo utilizzare
un qualunque processore XSLT scritto in un qualunque linguaggio. L'obiettivo
è quello di massimizzare la modularità ed è reso
particolarmente significativo dalle scarse prestazioni degli attuali
processori: deve essere possibile utilizzare in ogni momento quello
dalle prestazioni migliori.
- Il linguaggio utilizzato nell'implementazione è OCaml.
La scelta di utilizzare nuovamente OCaml semplifica l'integrazione
nell'interfaccia del proof-checker. Inoltre, mentre le caratteristiche
funzionali del linguaggio sono meno significative nell'ambito dello
sviluppo di interfacce grafiche, il sofisticato sistema di type-inference
unito alle feature object-oriented permettono di raggiungere elevati
livelli di produttività e di correttezza e pulizia del codice.
Figura 7.1: Grafo delle dipendenze per i moduli dell'interfaccia
Gtk
Pertanto, è stata scelta la divisione in moduli mostrata in figura
7.1, dove:
-
MmlInterface è il modulo radice, la cui interfaccia è
vuota, che si occupa della gestione dei widget e delle finestre che compongono
l'interfaccia grafica, invocando i (meta)moduli ProofChecker e XsltProcessor
per le elaborazioni.
- GtkMathView è il binding per OCaml del widget MathView, la
cui interfaccia è5
exception ErrorLoadingFile of string
class math_view_signals :
([> `container | `widget | `math_view] as 'b) Gtk.obj ->
object ('a)
method jump :
callback:(string -> unit) -> GtkSignal.id
end
class math_view :
Gtk_mathview.math_view Gtk.obj ->
object
method coerce : GObj.widget
method connect : math_view_signals
method get_selection : string option
method load : filename:string -> unit
end
val math_view :
?adjustmenth:GData.adjustment ->
?adjustmentv:GData.adjustment ->
?border_width:int ->
?width:int ->
?height:int ->
?packing:(GObj.widget -> unit) ->
?show:bool -> unit -> math_view
- ProofChecker è il metamodulo logico comprendente tutti
i moduli che compongono il proof-checker descritto nel capitolo
5.
- XsltProcessor è il modulo che fornisce il binding per
i processori XSLT e la cui interfaccia è:
(* (process filename usecache mode) calls the XSLT *)
(* processor on the XML file whose name is filename. *)
(* mode could be either "theory" or "cic" *)
(* If usecache is true and the result of the processing *)
(* is already in cache, then it is reused without *)
(* calling again the real XSLT processor. *)
process : string * bool * string -> string
Poiché è possibile effettuare il binding per OCaml esclusivamente di
funzioni scritte in C e poiché tutti gli attuali processori XSLT sono
scritti in Java, effettuare il binding per OCaml del codice Java è
un'operazione complessa e prona ad errori. Inoltre, non è pensabile
invocare ogni volta il processore XSLT da linea di comando, a causa del
tempo richiesto per il bootstrap della Java Virtual Machine e l'elaborazione
degli stylesheet. Pertanto, si è scelto di incapsulare i processori XSLT in
demoni UDP e di implementare il modulo XsltProcessor in
OCaml come un semplice client in grado di contattare tali demoni.
Figura 7.2: Protocollo di comunicazione fra il demone UDP con funzionalità di XSLT-processor e i client
In figura 7.2 viene mostrato il protocollo di comunicazione
utilizzato fra il client e il demone:
inputpath è il pathname del file XML al quale applicare le
trasformazioni, outputpath è il pathname richiesto per il file XML
ottenuto da tali
applicazioni. Grazie all'idempotenza delle trasformazioni XSLT e al fatto
che i file XML prodotti vengono mantenuti su disco fino alla chiusura
dell'interfaccia, è possibile ottenere un protocollo fault-tolerant
verso i guasti di comunicazione non bizantini semplicemente facendo
reiterare la richiesta al client ad intervalli regolari fino a quando non
riceve risposta, sotto il vincolo aggiuntivo che due richieste non possano
mai differire esclusivamente per l'inputpath; grazie al precedente vincolo
e all'utilizzo del disco come cache, nel caso che la stessa richiesta
giunga nuovamente al server a causa di un guasto o dell'eccessiva lentezza
di questo, l'overhead aggiuntivo consisterà esclusivamente nella rispedizione
al client della conferma dell'avvenuta elaborazione.
L'unica critica alla precedente soluzione consiste nell'osservazione che, in
tal modo, l'albero DOM ottenuto dalle trasformazioni XSLT deve essere
serializzato su disco per poi essere nuovamente sottoposto a parsing dal
widget MathView. Fino a quando il widget non esporrà un'interfaccia DOM
(o equivalente) e potrà esclusivamente utilizzare file su disco come
sorgenti, non ci saranno soluzioni alternative. Per questo motivo
è prevista una futura estensione del widget al fine di dotarlo di tale
funzionalità.
Seconda fase
Per trasformare l'interfaccia progettata nella prima fase in un prototipo
per la (ri)annotazione dei termini è necessario:
-
Fornire una rappresentazione interna dei termini annotati e un
cache per essi.
- Fornire un parser per i file di annotazioni.
- Fornire una funzione di salvataggio che, data la rappresentazione
interna dei termini annotati, crei il file XML contenente le annotazioni.
- Fornire un modulo che, data la rappresentazione interna di un termine
annotato e dato un XPointer, ritorni il nodo selezionato dall'XPointer.
- Fornire un modulo che, data la rappresentazione interna di un termine
e il riferimento ad uno dei nodi, ritorni la lista dei suggerimenti
da utilizzare per annotare tale nodo.
In questa fase, l'obiettivo non è quello di sviluppare un vero tool
per l'annotazione, ma esclusivamente quello di capire se un tale tool sia
realizzabile e quale sia la sua utilità (programmazione esplorativa).
Pertanto, la fase di progettazione è stata ridotta al minimo e si è deciso,
una volta capite le funzionalità necessarie, di abbandonare il
prototipo e ricominciare dalla fase di specifica. In questo lavoro, quindi,
non viene riportata la strutturazione in moduli del prototipo, nè le loro
interfacce, ancora soggette a cambiamenti continui. Indicativamente, comunque:
-
Per quanto riguarda i punti 1 e 2, al modulo Cic già sviluppato per il
proof-checker è stata aggiunta la nuova rappresentazione interna e sono
stati modificati per utilizzarla sia il metamodulo CicParser che il modulo
CicCache.
- Per implementare le funzioni dei punti 3 e 4 sono stati creati due nuovi
moduli, chiamati rispettivamente Cic2Xml e CicXPath, che espongono ognuno una
sola funzione e le cui interfacce sono ovvie. Il modulo CicXPath
riconosce esclusivamente il sottoinsieme banale di XPath effettivamente
utilizzato in HELM.
- Per implementare il punto 5 è stato creato un ulteriore modulo che
espone una sola funzione che restituisce come suggerimenti una lista ordinata
di stringhe di markup XML da associare ai pulsanti della palette.
7.2.2 Risultati ottenuti
Per quanto riguarda le funzionalità di proof-checking e resa, l'interfaccia
ha dato risultati incoraggianti: grazie all'utilizzo delle usuali notazioni
matematiche, della rappresentazione ad albero della libreria, della presenza
di collegamenti ipertestuali e dell'utilizzo del prototipo di generazione
automatica della descrizione in linguaggio naturale della prova, gli oggetti
della libreria standard di Coq possono essere finalmente piacevolmente
usufruiti6, anche se
l'interpretazione della maggior parte delle prove è ancora un'operazione
complessa, riservata ai conoscitori del sistema logico.
Per quanto riguarda l'utilizzo dell'interfaccia come prototipo per
la (ri)annotazione delle prove, i risultati ottenuti indicano
chiaramente la necessità di ristrutturare alcune delle componenti sviluppate
in precedenza. Infatti, nonostante il meccanismo dei suggerimenti risulti
promettente, la riannotazione di un termine è resa estremamente penosa
dalla necessità, ad ogni modifica, di esportare su file la nuova notazione,
riapplicare le trasformazioni presentazionali e riprocessare con il widget
il risultato ottenuto; complessivamente, queste operazioni possono richiedere
ogni volta anche alcuni minuti.
Per risolvere questo problema è necessario:
-
Ristrutturare gli stylesheet in modo che sia possibile applicarli ad
un sotto-termine.
- Dotare il widget di un'interfaccia DOM o equivalente che permetta
la modifica di una sotto-espressione.
- Riprogettare il prototipo in modo da utilizzare i precedenti meccanismi.
- 1
- http://xml.apache.org
- 2
- Xalan-C è il porting in C++ del processore Xalan-J
sviluppato nell'ambito dell'Apache XML Project e attualmente utilizzato da
Cocoon nei siti di presentazione del progetto HELM.
- 3
- Al momento, le teorie vengono rese giustapponendo
la rappresentazione dei singoli oggetti che le compongono.
- 4
- Gli hyperlink sono collegamenti conformi allo standard
XLink introdotti durante le trasformazioni dal formato del sistema logico
a quello content e successivamente propagati nella successiva trasformazione.
Non sono ancora riconosciuti dai browser standard e, pertanto, non sono
ancora usufruibili usando la precedente interfaccia.
- 5
- Vengono riportati solamente i metodi
effettivamente utilizzati, tranne quelli ereditati dalla superclasse
GContainer.container, che vengono tutti omessi.
- 6
- A patto di essere pazienti! Poiché viene utilizzato lo
stesso processore XSLT usato con Cocoon, le prestazioni sono deludenti
per le stesse motivazioni esposte a pagina 7.1.1.
Chapter 8 Conclusioni
Il problema dello sfruttamento delle nuove tecnologie basate su XML
per la memorizzazione, l'indicizzazione e la condivisione di documenti
matematici è destinato a diventare sempre più rilevante nel prossimo
futuro, quando, incentivata dall'introduzione di standard per la
visualizzazione e lo scambio di espressioni matematiche, quali MathML ed
OpenMath, la comunità scientifica inizierà a mettere in linea sul World
Wide Web librerie distribuite di documenti matematici.
Il solo progresso delle tecnologie Web non sarà, però, sufficiente
a soddisfare le aspettative degli utenti: al fine di poter verificare
la correttezza dei documenti e per permettere di effettuare ricerche complesse
all'interno delle librerie, diventa necessario considerare anche la semantica
dei documenti matematici; questa è l'argomento di studio della Logica Formale
e della Teoria della Dimostrazione, i cui prodotti concreti sono i
proof-assistant.
I proof-assistant, utilizzati fino ad ora da gruppi estremamente
ristretti di persone, non hanno subito l'evoluzione, trainata dalle nuove
tecnologie Web, a cui sono stati soggetti la maggior parte degli applicativi
software negli ultimi anni e che ha portato al passaggio dal modello
application-centric, in cui l'enfasi è posta sull'applicazione, a quello
document-centric, focalizzato sul documento; al contrario,
questi strumenti sono cresciuti negli anni in modo disorganizzato, comprendendo
sempre più funzionalità ed evolvendo in sistemi sempre più monolitici e
refrattari alle modifiche. Un altro aspetto negativo degli attuali
proof-assistant è che l'attenzione viene posta esclusivamente sugli aspetti
di provabilità dei teoremi, ovvero sulla ricerca delle dimostrazioni,
trascurando il prodotto di tale ricerca, che sono le prove stesse.
Lo scopo di questa tesi è quello di studiare l'integrazione di questi due
mondi al fine di rendere possibile la creazione di librerie distribuite di
conoscenza matematica formalizzata; come effetto collaterale, si ottiene
la ristrutturazione in chiave modulare dell'architettura dei proof-assistant.
Per raggiungere questo ambizioso obiettivo, è necessario affrontare numerosi
problemi, sia teorici che di natura tecnologica, alcuni dei quali privi di
soluzioni soddisfacenti.
Concretamente,
è stata proposta un'architettura generale comprendente strumenti per la
creazione, il mantenimento e lo sfruttamento di una libreria di questo tipo
e sono stati progettati e realizzati alcuni di questi strumenti per
dimostrare la realizzabilità del progetto e individuarne le problematiche.
Fra gli strumenti sviluppati vi sono stati:
-
un modulo per esportare teorie matematiche dal formato interno
utilizzato dal proof-assistant Coq ad un'opportuna istanza di XML;
- un proof-checker per gli oggetti matematici memorizzati in
formato XML;
- un sistema di stylesheet per la rimatematizzazione del contenuto
formale attraverso l'applicazione delle usuali notazioni matematiche
bidimensionali;
- tool per la gestione degli aspetti di distribuzione della libreria
(accesso ai documenti remoti);
- un'interfaccia Web e un'interfaccia in Gtk per il browsing della
libreria.
Durante la progettazione, l'enfasi è stata posta sulla facilità di
pubblicazione e accesso ai documenti della libreria e su quelle tematiche
che vengono normalmente trascurate negli attuali proof-assistant, quali
la visualizzazione delle prove.
Nella forma, il progetto è decisamente originale, anche se è correlato
a numerosi altri progetti nei campi del web-publishing, delle digital-library
e del proof-reasoning. Il lavoro più affine è il progetto MathWeb,
nato contemporaneamente e indipendentemente dal progetto HELM sviluppato
all'Università di Bologna e il cui nucleo iniziale è rappresentato
dal prodotto di questa tesi. Il prossimo paragrafo è dedicato ad un
confronto esaustivo dei due progetti; nel paragrafo 8.2,
infine, vengono elencati i possibili sviluppi futuri.
8.1 Confronto fra i progetti HELM e MathWeb
Il progetto MathWeb, coordinato dal Prof. Michael Kohlhase, è nato
recentemente come evoluzione del progetto Omega, di cui ha allargato
gli obiettivi e le finalità.
Omega è un progetto a lungo termine sviluppato presso Universität des
Saarlandes (città di Saarbrücken, Germania) dal gruppo del Prof.
Jörg Siekmann, attualmente composto da quattordici fra ricercatori e
professori, coadiuvati da una decina di studenti. Lo scopo del progetto
è lo sviluppo di un sistema in grado di incentivare l'utilizzo dei
theorem-prover nello sviluppo e nell'insegnamento della matematica.
L'architettura, pesantemente distribuita, prevede numerosi
sottosistemi, fra i quali un proof planner (pianificatore della prova),
tool per la formulazione di problemi, theorem-prover general-purpose o
specializzati in vari domini matematici, interfacce per l'utilizzo di
sistemi per la computer-algebra, generatori pseudo-automatici di dimostrazioni
per analogia e sofisticati meccanismi di intelligenza artificiale per la
presentazione delle prove in linguaggio naturale.
Le nuove tematiche affrontate da MathWeb rispetto al progetto Omega sono
quelle della memorizzazione delle teorie in linguaggio XML,
della pubblicazione on-line di librerie distribuite di documenti matematici e
della loro resa in formati standard di presentazione1.
Sebbene gli obiettivi di MathWeb siano molto più ambiziosi di quelli di Helm,
diversi aspetti possono essere proficuamente confrontati:
-
L'individuazione del contenuto informativo delle prove
- La presentazione delle prove
- Il formato di codifica dei documenti matematici
- Il modello di distribuzione
- I meccanismi di indicizzazione e ricerca
8.1.1 Il contenuto informativo delle prove
Mentre noi abbiamo individuato nei l-termini il vero contenuto
informativo delle dimostrazioni, in Omega non solo la prova, ma anche l'intero
processo con la quale è stata ottenuta è rilevante. Pertanto, quello che
in Omega viene salvato su disco è l'intero proof-plan, ovvero la storia della
dimostrazione, comprendente la sequenza di tattiche applicate e tutte le
informazioni rese disponibili dai tool invocati. Poiché Omega, per la
risoluzione di alcuni goal o la riduzione di espressioni matematiche,
si interfaccia con sistemi esterni, per esempio Maple, non sarebbe possibile
per il sistema la costruzione sistematica di un l-termine che abiti la
tesi. Pertanto,
la scelta di considerare l'intero proof-plan come contenuto informativo è
pienamente giustificabile.
D'altro canto, i l-termini di CIC, unico sistema logico
attualmente supportato da HELM, contengono indubbiamente tutta l'informazione
richiesta e questo giustifica la loro identificazione con il contenuto
informativo delle prove. La maggiore concisione e pulizia di HELM viene,
però, penalizzata durante la fase di presentazione delle prove.
8.1.2 La presentazione delle prove
In Omega, avendo a disposizione l'intero proof-plan, la generazione automatica
della descrizione in linguaggio naturale di una prova è sicuramente
facilitata rispetto a sistemi in cui il formato delle prove è meno
informativo. Indubbiamente, grazie all'utilizzo di tecniche evolute di
intelligenza artificiale, i risultati ottenuti in questo campo sono notevoli,
specie se confrontati con sistemi analoghi, come il modulo Natural
di Coq [CKT95].
In generale, comunque, la tecnologia attuale non sembra, e forse non
sarà mai, in grado di generare descrizioni che sembrino veramente naturali
per prove di notevole complessità.
In HELM il problema viene evitato ricorrendo alle
annotazioni informali, grazie alle quali l'utente ha la possibilità di
descrivere liberamente le prove formali. Questo approccio è suscettibile
di due critiche: la prima è che, in questo modo, non è garantita alcuna
corrispondenza fra la prova formale e la sua annotazione informale; la seconda
riguarda l'onere per l'utente di annotare ogni prova, compito estremamente
complesso se effettuato successivamente alla ricerca della dimostrazione
formale. Per quanto riguarda la prima critica, la possibilità di richiamare
il proof-checker sulla prova formale ne garantisce la correttezza, mentre
la possibilità di deannotare progressivamente il l-termine permette
di individuare le discrepanze fra le due descrizioni. In presenza di
dimostrazioni complesse, inoltre, la dimostrazione ottenuta
automaticamente potrebbe essere cosí difficile da comprendere da diventare
inutile, mentre la leggibilità di quella annotata è sotto
il diretto controllo dell'utente. A parte questi casi estremi, comunque, la
critica rimane fondata, anche se il feeling dell'autore è che i matematici
possano sempre preferire una dimostrazione informale, eventualmente inesatta, ma
scritta con l'acume e la sensibilità dell'umano rispetto a quella,
sicuramente corretta ma artificiosa, generata automaticamente.
Inoltre, un importante punto a favore della scelta di
HELM è la possibilità, da parte dei singoli utenti, di riannotare a
piacimento le dimostrazioni. Per esempio, ciò che può essere ovvio per
l'autore può non esserlo per chi legge la dimostrazione, che può scegliere
di deannotare la parte di dimostrazione che non capisce e riannotarla in
maniera differente.
Questa possibilità, indubbiamente auspicabile, è ovviamente interdetta nei
sistemi che generano automaticamente la dimostrazione in linguaggio naturale.
La seconda critica, quella sulla difficoltà di annotare le prove, è invece
largamente infondata per due motivi. Il primo è che l'uso delle annotazioni
non impedisce la loro generazione tramite strumenti automatici, che possono
eventualmente sfruttare anche informazione non contenuta nel l-termine,
come la sequenza delle tattiche. In questo senso, possiamo dire che la
generazione automatica della presentazione di una prova in linguaggio naturale
è solo un caso particolare della scrittura di una annotazione. Inoltre,
le annotazioni potrebbero essere generate, automaticamente o manualmente,
durante la scrittura delle prove, permettendo una descrizione massimamente
fedele al ragionamento effettuato. Il secondo motivo riguarda la possibilità
di semplificare la procedura ricorrendo a tool dotati di elaborate interfacce
grafiche e in grado di prevenire l'utente suggerendogli la giusta sequenza
di annotazione.
8.1.3 Il formato dei documenti matematici
Mentre HELM si affida ad un generico formato XML per i documenti formali ed
a MathML per la loro rappresentazione semi-formale, per
Omega2
si è scelto un formato proprietario delle prove, che vengono
scritte in Allegro Lisp; MathWeb, invece, adotta un'estensione non standard di
OpenMath per la rappresentazione dei documenti matematici, chiamata OmDoc.
La scelta
del formato proprietario per le prove è coerente con la visione distribuita,
ma essenzialmente application-centric, di Omega: il gestore del proof-plan,
il vero cuore di Omega, può connettersi a diversi tool esterni per la
ricerca delle prove; per poter lavorare sulle prove, però, è necessario
ricorrere a questo strumento. Pertanto, Omega è suscettibile alle
critiche al software application-centric (vedi paragrafo 1.2.2),
mentre HELM, che aderisce al paradigma content-centric, ne è immune.
Per quanto riguarda il formato di rappresentazione dei documenti matematici,
necessariamente contenenti descrizioni delle prove, la scelta di MathWeb è
caduta su OpenMath. Poiché in Omega non vi è una rappresentazione XML
delle prove, era necessario per loro trovare un formato che potesse
codificare sia la presentazione, che la semantica semi-formale delle
espressioni matematiche: l'unico standard che soddisfa queste richieste è
OpenMath. Per quanto riguarda HELM, invece, la presenza dei file XML che
mantengono il l-termine formale permette di utilizzare MathML content
come rappresentazione semi-formale, con in più la possibilità di seguire
gli XLink per risalire alla semantica formale. Entrambe le scelte hanno dovuto
affrontare problemi analoghi, ovvero la trasformazione dei documenti
semi-formali in un opportuno formato di presentazione e il problema della
rappresentazione del livello degli oggetti. Per le trasformazioni, entrambi
i gruppi di sviluppo hanno optato per la scelta standard di stylesheet XSLT,
utilizzando HTML o MathML presentation come formati di
output3.
Più interessante è il confronto fra le soluzioni adottate per affrontare
il problema che sia MathML che OpenMath sono nati per codificare
espressioni e non interi documenti matematici contenenti, per esempio,
definizioni e teoremi. La scelta di MathWeb
è stata la definizione di un'opportuna estensione di OpenMath, chiamata OMDoc:
i documenti OMDoc comprendono non solo oggetti matematici, ma anche i
corrispondenti metadati e frammenti di stylesheet XSLT utilizzati per fini
presentazionali.
I principali elementi XML di OMDoc per descrivere oggetti matematici sono
annotazioni informali, definizioni, teoremi, esempi ed esercizi.
Attributi vengono utilizzati, per esempio,
per classificare ulteriormente teoremi in lemmi, corollari, etc.
Per quanto riguarda i metadati, fra i quali sono presenti quelli Dublin
Core, è impossibile non criticare la scelta di codificarli non
utilizzando lo standard RDF. Complessivamente, è criticabile la scelta
di affiancare nello stesso documento dati, metadati e presentazione: poiché,
tipicamente, le applicazioni sono interessate esclusivamente ad uno di questi
aspetti alla volta, questo le costringe ad un inutile parsing di informazione
inutilizzata. Inoltre, in questo modo si rinuncia all'importante
separazione del contenuto dalla presentazione, che rappresenta uno degli
obiettivi principali dell'introduzione degli standard XML e XSL. Sotto questo
aspetto, l'architettura di HELM, che prevede la separazione in file distinti
di metadati, notazioni e oggetti, con l'aggiunta di teorie per assemblare
e strutturare questi ultimi, risulta essere molto più pulita. Inoltre,
in questo modo, è possibile definire teorie distinte basate sugli stessi
oggetti senza doverli replicare. Il prezzo da pagare è la perdita
dell'unità del documento, che costringe sovente al downloading di numerosi
file e all'utilizzo massiccio di XLink. Mentre il secondo punto non rappresenta
un vero problema, il primo può essere risolto implementando getter più
elaborati, in grado di richiedere il download contemporaneo di diversi file,
che possono essere compressi durante la trasmissione (vedi 4.1).
Questa soluzione, però,
richiede un'attiva collaborazione da parte dei server di distribuzione,
contravvenendo al terzo requisito di HELM (vedi paragrafo 1.3.1).
8.1.4 Il modello di distribuzione
Gli obiettivi dei modelli di distribuzione di HELM (vedi capitolo
4)
e MathWeb sono profondamente diversi. Brevemente, MathWeb si propone di
affrontare il problema dei diritti d'autore sui documenti scientifici
presenti in rete. Per questo motivo, viene richiesta l'esistenza in rete di
una e una sola copia per ogni documento. È possibile la migrazione della
copia: per esempio, quando l'autore pubblica l'articolo, la copia deve
migrare dal suo server a quello dell'editore. Per evitare la rottura di
collegamenti fra documenti a causa della migrazione delle copie, sono
previsti appositi puntatori dalle precedenti locazioni all'attuale.
Poiché l'esistenza di una sola copia crea inevitabili colli di bottiglia,
vengono proposti meccanismi di caching per aumentare le prestazioni.
Infine, è prevista la possibilità di rendere obsoleto un documento
(per esempio, a causa di definizioni errate).
Le critiche al modello di MathWeb sono innumerevoli. In primo luogo, l'esistenza
di un'unica copia che viene fatta migrare è soggetta a tipiche problematiche
di fault-tolerance: la migrazione è rischiosa e il server che mantiene
l'unica copia è un ``single point of failure''. Il sistema di puntatori
richiede meccanismi di path compression per evitare la creazione di lunghe
catene per giungere alla copia cercata e, poiché i documenti possono
essere modificati (rendendoli obsoleti), opportune politiche debbono
essere implementate per sincronizzare i cache. Durante partizionamenti
della rete, la sincronizzazione può essere perduta o, peggio,
l'informazione sulla locazione dell'unica copia potrebbe diventare obsoleta,
con conseguente impatto, per esempio,
sui diritti economici di accesso al documento. Infine, chiunque voglia
pubblicare o accedere ad un articolo deve avere a disposizione un host su cui
sia installato un server MathWeb. Si confronti quest'ultima osservazione con
gli antitetici requisiti di HELM (paragrafo 1.3.1).
Ferme restando le differenze fra gli obiettivi dei due modelli di distribuzione,
quello di MathWeb mette in luce due mancanze di HELM. La prima è
l'impossibilità di rendere obsoleto un documento. La soluzione più
semplice, ma anche scarsamente soddisfacente, sarebbe allestire uno o più
server che mantengano la lista dei documenti obsoleti.
Il secondo è la mancanza di garanzie sull'esistenza di un documento
referenziato da un secondo; in particolare, se costruisco una teoria A
basandomi su definizioni e teoremi date in una teoria B, quando
l'ultima copia di B viene cancellata tutte le copie di A perdono di
significato. Supporre che esista per sempre almeno una
copia di ogni documento è quantomeno utopistico. Pertanto, è ragionevole
supporre che, se sono interessato ad un documento A di cui esistono poche
copie, me ne memorizzi una su disco per evitarne la perdita, mettendola, poi, a
diposizione di tutti. Quindi, il
requisito di HELM che prevede l'esistenza di più copie di uno stesso
documento, tutte identificate dallo stesso nome logico, risolve concretamente
il problema. Per inciso, in questo modo avviene una naturale selezione dei
documenti sulla base della loro rilevanza: quelli scarsamente referenziati
verranno prima o poi cancellati, mentre quelli interessanti aumenteranno la
loro diffusione.
8.1.5 I meccanismi di indicizzazione e ricerca
I due progetti differiscono notevolmente anche per quanto riguarda i
meccanismi di indicizzazione e ricerca.
HELM adotta il tradizionale approccio dei
motori di ricerca, che visitano i siti di distribuzione indicizzandone
efficacemente i documenti grazie all'utilizzo di metadati descritti nello
standard RDF. Comuni browser possono quindi essere utilizzati per contattare
i motori di ricerca. MathWeb, al contrario, non prevede motori di ricerca,
ma affida l'indicizzazione dei documenti ai server già introdotti dal
modello di distribuzione. In questo modo, le query non vengono effettuate
ad un singolo server, ma, attraverso un programma apposito, devono essere
contattati tutti quelli esistenti. La risoluzione della query diventa
quindi un problema distribuito, reso mediamente complesso dalle richieste
prestazionali in presenza di un gran numero di server. Questa architettura,
abbastanza complessa, non è sicuramente giustificata da problemi di fault
tolerance, risolvibili attraverso l'utilizzo di un numero sufficiente di
(istanze di) motori di ricerca. Anzi, la caduta di un server impedisce perfino
la ricerca sui documenti ivi conservati.
In compenso, l'elevata complessità computazionale della risoluzione di
query per niente banali, come quelle presentate a pagina 1,
necessita di sistemi distribuiti con bilanciamento del carico e ricerche in
parallelo, simili a quelli di MathWeb.
Nel modello di HELM, questo problema non viene trascurato, ma semplicemente
scaricato sull'architettura del motore di ricerca, per la quale si possono
adottare soluzioni analoghe a quelle di sistemi come Yahoo o Altavista, che
sono in grado di soddisfare migliaia di richieste contemporaneamente.
8.2 Lavori Futuri
Grazie agli ambiziosi obiettivi del progetto, sono possibili numerosi
sviluppi del lavoro svolto finora; alcuni sono mirati al miglioramento
e al consolidamento di quanto già realizzato e richiedono collaborazione
da parte di altri gruppi di ricerca, come il team responsabile dello sviluppo
di Coq; altri sono estensioni del sistema al fine di considerare le
problematiche che non sono ancora state affrontate, quali l'indicizzazione
tramite metadati dei documenti della libreria e i meccanismi di ricerca.
Infine, affinché l'intero progetto possa considerarsi avviato con successo,
è necessario che si formi una comunità di utenti e che nuovi gruppi di
sviluppo integrino nell'architettura generale gli strumenti per la
gestione di formalismi logici diversi da CIC. Segue una rassegna dei
principali sviluppi possibili:
-
Architettura generale
-
Per verificare la validità dell'architettura generale di HELM, è
necessario considerare almeno un altro sistema logico, diverso da CIC,
e sviluppare per esso i moduli corrispondenti a quelli già implementati
per CIC.
- Modulo di esportazione da Coq
-
Al fine di esportare in modo corretto tutta l'informazione necessaria,
eliminando la necessità di ricorrere alla successiva fase di
riparazione dei file, è necessaria una stretta collaborazione con il
team di sviluppo di Coq, già prevista per l'autunno 2000. In tale
occasione, si provvederà anche all'adozione di alcune nuove estensioni
a CIC, previste per la nuova versione di Coq, fra le quali l'introduzione
di un costrutto di naming, che risulterà utile anche per la resa delle
prove, e la sostituzione del meccanismo di cottura con un altro più
semplice, ma ad esso equivalente.
- Getter
-
Nei due getter già sviluppati potranno essere integrate le rimanenti
funzionalità opzionali descritte nel paragrafo 4.1. Inoltre,
potrà essere necessario rivedere il meccanismo di sintesi dei documenti
a mano a mano che aumenta il numero degli eventuali file sorgenti
(oggetto, dei tipi sintetizzati, contenenti annotazioni, etc.).
- CIC Proof-checker
-
Per completare l'implementazione del proof-checker, è necessario considerare
la gestione del livello degli universi. Inoltre, una volta aggiornato il
meccanismo di esportazione da Coq alla versione 7.0, sarà
necessario modificare l'intero proof-checker per utilizzare le nuove
estensioni a CIC.
- Stylesheet notazionali
-
Oltre all'aggiornamento degli stylesheet di default dovuto alle nuove
estensioni di CIC, rimane da valutare la realizzabilità di un meccanismo
per la generazione semi-automatica degli stylesheet forniti dagli utenti.
- Meccanismi di annotazione
-
È necessario superare i problemi tecnologici che rendono quasi
inutilizzabile l'attuale prototipo per l'annotazione, al fine di
poter intraprendere un periodo di sperimentazione per individuare
le problematiche legate all'annotazione e la sua effettiva
importanza per la rappresentazione delle prove in linguaggio naturale.
- Sviluppo di proof-assistant
-
Un interessante sviluppo, inizialmente non previsto, consiste
nell'implementazione di un proof-assistant modulare basato sul formato
XML di rappresentazione dei dati. L'enfasi verrebbe posta sulla
naturalezza dei l-termini generati dalle tattiche, al fine
di produrre prove facilmente annotabili e simili alle corrispondenti
prove cartacee non formalizzate. Inoltre, potrebbe essere investigata
la possibilità di annotare il termine durante la ricerca della prova.
- Meccanismi di indicizzazione e ricerca
-
Debbono ancora essere completamente sviluppati, anche se sono già chiare
le linee guida da seguire.
- Comunicazione dell'informazione fra differenti sistemi logici
-
Una volta che il progetto sia ben avviato e siano stati sviluppati gli
strumenti affinché più sistemi logici possano contribuire alla libreria,
si potrà affrontare il problema più profondo sollevato dalla creazione
di librerie di documenti matematici codificati in formalismi eterogenei,
ovvero quello dell'uso nelle dimostrazioni di definizioni e teoremi dati
in un diverso formalismo.
- 1
- Al momento della
pubblicazione di questa tesi, la ristrutturazione del progetto Omega in due
progetti distinti, Omega e MathWeb, non è ancora terminata e non è del
tutto chiaro quale progetto affronterà alcune problematiche.
Nel resto del capitolo, la cui prima stesura risale a prima dell'inizio della
scissione, i due progetti vengono talvolta identificati.
- 2
- Le caratteristiche
di Omega descritte in questo paragrafo sono prese da una serie di documenti
trovati sul sito del progetto e ora non più on-line a causa della sua
ristrutturazione. Pertanto, le informazioni date potrebbero essere obsolete.
- 3
- MathWeb fornisce anche uno stylesheet verso LATEX. Tale
trasformazione può essere ottenuta facilmente applicando in cascata lo
stylesheet per ottenere MathML presentation e uno di quelli, disponibili in
rete, per passare da questo formato a LATEX; lo stylesheet verso MathML,
previsto in MathWeb, non è però ancora stato scritto.
Appendix A Il DTD per il livello dei termini e degli oggetti di CIC
<?xml encoding="ISO-8859-1"?>
<!--*****************************************************************-->
<!-- DTD FOR CIC OBJECTS: -->
<!-- First draft: September 1999, Claudio Sacerdoti Coen -->
<!-- Revised: February 3 2000, Claudio Sacerdoti Coen, Irene Schena -->
<!-- Next Revision: April 4 2000, Claudio Sacerdoti Coen -->
<!-- Next Revision: June 19 2000, Claudio Sacerdoti Coen -->
<!-- Last Revision: June 20 2000, Claudio Sacerdoti Coen -->
<!--*****************************************************************-->
<!-- CIC term declaration -->
<!ENTITY % term '(LAMBDA|CAST|PROD|REL|SORT|APPLY|VAR|META|CONST|
MUTIND|MUTCONSTRUCT|MUTCASE|FIX|COFIX)'>
<!-- CIC objects: -->
<!ELEMENT Definition (body, type)>
<!ATTLIST Definition
name CDATA #REQUIRED
params CDATA #REQUIRED
paramMode (POSSIBLE) #IMPLIED
id ID #REQUIRED>
<!ELEMENT Axiom (type)>
<!ATTLIST Axiom
name CDATA #REQUIRED
params CDATA #REQUIRED
id ID #REQUIRED>
<!ELEMENT CurrentProof (Conjecture*,body,type)>
<!ATTLIST CurrentProof
name CDATA #REQUIRED
id ID #REQUIRED>
<!ELEMENT InductiveDefinition (InductiveType+)>
<!ATTLIST InductiveDefinition
noParams NMTOKEN #REQUIRED
params CDATA #REQUIRED
id ID #REQUIRED>
<!ELEMENT Variable (type)>
<!ATTLIST Variable
name CDATA #REQUIRED
id ID #REQUIRED>
<!-- Elements used in CIC objects, which are not terms: -->
<!ELEMENT InductiveType (arity,Constructor*)>
<!ATTLIST InductiveType
name CDATA #REQUIRED
inductive (true|false) #REQUIRED>
<!ELEMENT Conjecture %term;>
<!ATTLIST Conjecture
no NMTOKEN #REQUIRED>
<!ELEMENT Constructor %term;>
<!ATTLIST Constructor
name CDATA #REQUIRED>
<!-- CIC terms: -->
<!ELEMENT LAMBDA (source,target)>
<!ATTLIST LAMBDA
id ID #REQUIRED>
<!ELEMENT PROD (source,target)>
<!ATTLIST PROD
id ID #REQUIRED>
<!ELEMENT CAST (term,type)>
<!ATTLIST CAST
id ID #REQUIRED>
<!ELEMENT REL EMPTY>
<!ATTLIST REL
value NMTOKEN #REQUIRED
binder CDATA #REQUIRED
id ID #REQUIRED>
<!ELEMENT SORT EMPTY>
<!ATTLIST SORT
value CDATA #REQUIRED
id ID #REQUIRED>
<!ELEMENT APPLY (%term;)+>
<!ATTLIST APPLY
id ID #REQUIRED>
<!ELEMENT VAR EMPTY>
<!ATTLIST VAR
relUri CDATA #REQUIRED
id ID #REQUIRED>
<!ELEMENT META EMPTY>
<!ATTLIST META
no NMTOKEN #REQUIRED
id ID #REQUIRED>
<!ELEMENT CONST EMPTY>
<!ATTLIST CONST
uri CDATA #REQUIRED
id ID #REQUIRED>
<!ELEMENT MUTIND EMPTY>
<!ATTLIST MUTIND
uri CDATA #REQUIRED
noType NMTOKEN #REQUIRED
id ID #REQUIRED>
<!ELEMENT MUTCONSTRUCT EMPTY>
<!ATTLIST MUTCONSTRUCT
uri CDATA #REQUIRED
noType NMTOKEN #REQUIRED
noConstr NMTOKEN #REQUIRED
id ID #REQUIRED>
<!ELEMENT MUTCASE (patternsType,inductiveTerm,pattern*)>
<!ATTLIST MUTCASE
uriType CDATA #REQUIRED
noType NMTOKEN #REQUIRED
id ID #REQUIRED>
<!ELEMENT FIX (FixFunction+)>
<!ATTLIST FIX
noFun NMTOKEN #REQUIRED
id ID #REQUIRED>
<!ELEMENT COFIX (CofixFunction+)>
<!ATTLIST COFIX
noFun NMTOKEN #REQUIRED
id ID #REQUIRED>
<!-- Elements used in CIC terms: -->
<!ELEMENT FixFunction (type,body)>
<!ATTLIST FixFunction
name CDATA #REQUIRED
recIndex NMTOKEN #REQUIRED>
<!ELEMENT CofixFunction (type,body)>
<!ATTLIST CofixFunction
name CDATA #REQUIRED>
<!-- Sintactic sugar for CIC terms and for CIC objects: -->
<!ELEMENT source %term;>
<!ELEMENT target %term;>
<!ATTLIST target
binder CDATA #IMPLIED>
<!ELEMENT term %term;>
<!ELEMENT type %term;>
<!ELEMENT arity %term;>
<!ELEMENT patternsType %term;>
<!ELEMENT inductiveTerm %term;>
<!ELEMENT pattern %term;>
<!ELEMENT body %term;>
Appendix B La rappresentazione OCaml dei termini e degli oggetti CIC
type sort =
Prop
| Set
| Type
and name =
Name of string
| Anonimous
and term =
Rel of int (* DeBrujin index *)
| Var of UriManager.uri (* base uri, name *)
| Meta of int (* numeric id *)
| Sort of sort (* sort *)
| Cast of term * term (* value, type *)
| Prod of name * term * term (* binder, source, target *)
| Lambda of name * term * term (* binder, source, target *)
| Appl of term list (* arguments *)
| Const of UriManager.uri * int (* uri, number of cookings*)
| MutInd of UriManager.uri * int * int (* uri, cookingsno, typeno*)
| MutConstruct of UriManager.uri * int * (* uri, cookingsno, *)
int * int (* typeno, consno *)
| MutCase of UriManager.uri * int * (* ind. uri, cookingsno, *)
int * (* ind. typeno, *)
term * term * (* outtype, ind. term *)
term list (* patterns *)
| Fix of int * inductiveFun list (* funno, functions *)
| CoFix of int * coInductiveFun list (* funno, functions *)
and obj =
Definition of string * term * term * (* id, value, type, *)
(int * UriManager.uri list) list (* parameters *)
| Axiom of string * term *
(int * UriManager.uri list) list (* id, type, parameters *)
| Variable of string * term (* name, type *)
| CurrentProof of string * (int * term) list * (* name, conjectures, *)
term * term (* value, type *)
| InductiveDefinition of inductiveType list * (* inductive types, *)
(int * UriManager.uri list) list * int (* parameters, n ind. pars *)
and inductiveType =
string * bool * term * (* typename, inductive, arity *)
constructor list (* constructors *)
and constructor =
string * term * bool list option ref (* id, type, really recursive *)
and inductiveFun =
string * int * term * term (* name, ind. index, type, body *)
and coInductiveFun =
string * term * term (* name, type, body *)
;;
Appendix C Un esempio di file XML per un oggetto CIC
<?xml version="1.0" encoding="ISO-8859-1"?>
<!DOCTYPE Definition SYSTEM "http://localhost:8081/getdtd?url=cic.dtd">
<Definition name="easy" id="i0" params="">
<body>
<LAMBDA id="i1">
<source>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0" id="i2"/>
</source>
<target binder="n">
<APPLY id="i3">
<CONST uri="cic:/Datatypes/nat_ind.con" id="i4"/>
<LAMBDA id="i5">
<source>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0" id="i6"/>
</source>
<target binder="n0">
<APPLY id="i7">
<MUTIND uri="cic:/Logic/or.ind" noType="0" id="i8"/>
<APPLY id="i9">
<MUTIND uri="cic:/Logic/eq.ind" noType="0" id="i10"/>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0"
id="i11"/>
<REL value="1" binder="n0" id="i12"/>
<MUTCONSTRUCT uri="cic:/Datatypes/nat.ind" noType="0"
noConstr="1" id="i13"/>
</APPLY>
<APPLY id="i14">
<MUTIND uri="cic:/Logic/ex.ind" noType="0" id="i15"/>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0"
id="i16"/>
<LAMBDA id="i17">
<source>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0"
id="i18"/>
</source>
<target binder="m">
<APPLY id="i19">
<MUTIND uri="cic:/Logic/eq.ind" noType="0"
id="i20"/>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0"
id="i21"/>
<APPLY id="i22">
<CONST uri="cic:/Peano/plus.con" id="i23"/>
<APPLY id="i24">
<MUTCONSTRUCT uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="2" id="i25"/>
<MUTCONSTRUCT uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="1" id="i26"/>
</APPLY>
<REL value="1" binder="m" id="i27"/>
</APPLY>
<REL value="2" binder="n0" id="i28"/>
</APPLY>
</target>
</LAMBDA>
</APPLY>
</APPLY>
</target>
</LAMBDA>
<APPLY id="i29">
<MUTCONSTRUCT uri="cic:/Logic/or.ind" noType="0"
noConstr="1" id="i30"/>
<APPLY id="i31">
<MUTIND uri="cic:/Logic/eq.ind" noType="0" id="i32"/>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0" id="i33"/>
<MUTCONSTRUCT uri="cic:/Datatypes/nat.ind" noType="0"
noConstr="1" id="i34"/>
<MUTCONSTRUCT uri="cic:/Datatypes/nat.ind" noType="0"
noConstr="1" id="i35"/>
</APPLY>
<APPLY id="i36">
<MUTIND uri="cic:/Logic/ex.ind" noType="0" id="i37"/>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0" id="i38"/>
<LAMBDA id="i39">
<source>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0"
id="i40"/>
</source>
<target binder="m">
<APPLY id="i41">
<MUTIND uri="cic:/Logic/eq.ind" noType="0"
id="i42"/>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0"
id="i43"/>
<APPLY id="i44">
<CONST uri="cic:/Peano/plus.con" id="i45"/>
<APPLY id="i46">
<MUTCONSTRUCT uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="2" id="i47"/>
<MUTCONSTRUCT uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="1" id="i48"/>
</APPLY>
<REL value="1" binder="m" id="i49"/>
</APPLY>
<MUTCONSTRUCT uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="1" id="i50"/>
</APPLY>
</target>
</LAMBDA>
</APPLY>
<APPLY id="i51">
<MUTCONSTRUCT uri="cic:/Logic/eq.ind" noType="0"
noConstr="1" id="i52"/>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0" id="i53"/>
<MUTCONSTRUCT uri="cic:/Datatypes/nat.ind" noType="0"
noConstr="1" id="i54"/>
</APPLY>
</APPLY>
<LAMBDA id="i55">
<source>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0" id="i56"/>
</source>
<target binder="n0">
<LAMBDA id="i57">
<source>
<APPLY id="i58">
<MUTIND uri="cic:/Logic/or.ind" noType="0"
id="i59"/>
<APPLY id="i60">
<MUTIND uri="cic:/Logic/eq.ind" noType="0"
id="i61"/>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0"
id="i62"/>
<REL value="1" binder="n0" id="i63"/>
<MUTCONSTRUCT uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="1" id="i64"/>
</APPLY>
<APPLY id="i65">
<MUTIND uri="cic:/Logic/ex.ind" noType="0"
id="i66"/>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0"
id="i67"/>
<LAMBDA id="i68">
<source>
<MUTIND uri="cic:/Datatypes/nat.ind"
noType="0" id="i69"/>
</source>
<target binder="m">
<APPLY id="i70">
<MUTIND uri="cic:/Logic/eq.ind" noType="0"
id="i71"/>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0"
id="i72"/>
<APPLY id="i73">
<CONST uri="cic:/Peano/plus.con"
id="i74"/>
<APPLY id="i75">
<MUTCONSTRUCT
uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="2" id="i76"/>
<MUTCONSTRUCT
uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="1" id="i77"/>
</APPLY>
<REL value="1" binder="m" id="i78"/>
</APPLY>
<REL value="2" binder="n0" id="i79"/>
</APPLY>
</target>
</LAMBDA>
</APPLY>
</APPLY>
</source>
<target binder="H">
<APPLY id="i80">
<MUTCONSTRUCT uri="cic:/Logic/or.ind" noType="0"
noConstr="2" id="i81"/>
<APPLY id="i82">
<MUTIND uri="cic:/Logic/eq.ind" noType="0"
id="i83"/>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0"
id="i84"/>
<APPLY id="i85">
<MUTCONSTRUCT uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="2" id="i86"/>
<REL value="2" binder="n0" id="i87"/>
</APPLY>
<MUTCONSTRUCT uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="1" id="i88"/>
</APPLY>
<APPLY id="i89">
<MUTIND uri="cic:/Logic/ex.ind" noType="0"
id="i90"/>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0"
id="i91"/>
<LAMBDA id="i92">
<source>
<MUTIND uri="cic:/Datatypes/nat.ind"
noType="0" id="i93"/>
</source>
<target binder="m">
<APPLY id="i94">
<MUTIND uri="cic:/Logic/eq.ind" noType="0"
id="i95"/>
<MUTIND uri="cic:/Datatypes/nat.ind"
noType="0" id="i96"/>
<APPLY id="i97">
<CONST
uri="cic:/Peano/plus.con" id="i98"/>
<APPLY id="i99">
<MUTCONSTRUCT
uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="2" id="i100"/>
<MUTCONSTRUCT
uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="1" id="i101"/>
</APPLY>
<REL value="1" binder="m" id="i102"/>
</APPLY>
<APPLY id="i103">
<MUTCONSTRUCT
uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="2" id="i104"/>
<REL value="3" binder="n0" id="i105"/>
</APPLY>
</APPLY>
</target>
</LAMBDA>
</APPLY>
<APPLY id="i106">
<MUTCONSTRUCT uri="cic:/Logic/ex.ind" noType="0"
noConstr="1" id="i107"/>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0"
id="i108"/>
<LAMBDA id="i109">
<source>
<MUTIND uri="cic:/Datatypes/nat.ind"
noType="0" id="i110"/>
</source>
<target binder="m">
<APPLY id="i111">
<MUTIND uri="cic:/Logic/eq.ind" noType="0"
id="i112"/>
<MUTIND uri="cic:/Datatypes/nat.ind"
noType="0" id="i113"/>
<APPLY id="i114">
<MUTCONSTRUCT
uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="2" id="i115"/>
<REL value="1" binder="m" id="i116"/>
</APPLY>
<APPLY id="i117">
<MUTCONSTRUCT
uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="2" id="i118"/>
<REL value="3" binder="n0" id="i119"/>
</APPLY>
</APPLY>
</target>
</LAMBDA>
<REL value="2" binder="n0" id="i120"/>
<APPLY id="i121">
<MUTCONSTRUCT uri="cic:/Logic/eq.ind"
noType="0" noConstr="1" id="i122"/>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0"
id="i123"/>
<APPLY id="i124">
<MUTCONSTRUCT uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="2" id="i125"/>
<REL value="2" binder="n0" id="i126"/>
</APPLY>
</APPLY>
</APPLY>
</APPLY>
</target>
</LAMBDA>
</target>
</LAMBDA>
<REL value="1" binder="n" id="i127"/>
</APPLY>
</target>
</LAMBDA>
</body>
<type>
<CAST id="i128">
<term>
<PROD id="i129">
<source>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0" id="i130"/>
</source>
<target binder="n">
<APPLY id="i131">
<MUTIND uri="cic:/Logic/or.ind" noType="0" id="i132"/>
<APPLY id="i133">
<MUTIND uri="cic:/Logic/eq.ind" noType="0" id="i134"/>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0"
id="i135"/>
<REL value="1" binder="n" id="i136"/>
<MUTCONSTRUCT uri="cic:/Datatypes/nat.ind" noType="0"
noConstr="1" id="i137"/>
</APPLY>
<APPLY id="i138">
<MUTIND uri="cic:/Logic/ex.ind" noType="0" id="i139"/>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0"
id="i140"/>
<LAMBDA id="i141">
<source>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0"
id="i142"/>
</source>
<target binder="m">
<APPLY id="i143">
<MUTIND uri="cic:/Logic/eq.ind" noType="0"
id="i144"/>
<MUTIND uri="cic:/Datatypes/nat.ind" noType="0"
id="i145"/>
<APPLY id="i146">
<CONST uri="cic:/Peano/plus.con" id="i147"/>
<APPLY id="i148">
<MUTCONSTRUCT uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="2" id="i149"/>
<MUTCONSTRUCT uri="cic:/Datatypes/nat.ind"
noType="0" noConstr="1" id="i150"/>
</APPLY>
<REL value="1" binder="m" id="i151"/>
</APPLY>
<REL value="2" binder="n" id="i152"/>
</APPLY>
</target>
</LAMBDA>
</APPLY>
</APPLY>
</target>
</PROD>
</term>
<type>
<SORT value="Prop" id="i153"/>
</type>
</CAST>
</type>
</Definition>
Bibliografia
- [APSSa]
-
Asperti A., Padovani L., Sacerdoti Coen C., and Schena I.
Content Centric Logical Environments.
Short Presentation at LICS 2000.
- [APSSb]
-
Asperti A., Padovani L., Sacerdoti Coen C., and Schena I.
Formal Mathematics in MathML.
To be presented at MathML International Conference 2000.
- [APSSc]
-
Asperti A., Padovani L., Sacerdoti Coen C., and Schena I.
Towards a Library of Formal Mathematics.
Accepted at TPHTOOLS 2000.
- [APSSd]
-
Asperti A., Padovani L., Sacerdoti Coen C., and Schena I.
XML, Stylesheets and the re-mathematization of formal content.
Submitted to LPAR 2000.
- [Bar92]
-
Barendregt H.
Lambda Calculi with Types.
In Abramsky, Samson and others, editor, Handbook of Logic in
Computer Science, volume 2. Oxford University Press, 1992.
- [BBC+97]
-
Barras B., Boutin S., Cornes C., Courant J., Filliatre J. C.,
Giménez E., Herbelin H., Huet G., Munoz C., Murthy C., Parent
C., Paulin-Mohring C., Saibi A., and Werner B.
The Coq Proof Assistant Reference Manual : Version 6.1.
Technical Report RT-0203, Inria (Institut National de Recherche en
Informatique et en Automatique), France, 1997.
- [Ber89]
-
Berners-Lee T.
Information Management: A Proposal.
1989.
- [BW97]
-
Barras B. and Werner B.
Coq in Coq.
Submitted, 1997.
- [CKT95]
-
Coscoy Y., Kahn G., and Thery L.
Extracting Text from Proofs.
Technical Report RR-2459, Inria (Institut National de Recherche en
Informatique et en Automatique), France, 1995.
- [Coq86]
-
Coquand T.
An Analysis of Girard's Paradox.
In Symposium on Logic in Computer Science, Cambridge, 1986. MA.
IEEE press.
- [dBr80]
-
de Bruijn N. G.
A survey of the project AUTOMATH.
In J. P. Seldin and J. R. Hindley, editors, To H. B. Curry:
Essays in Combinatory Logic, Lambda Calculus and Formalism, pages 589--606.
Academic Press, 1980.
- [Geu93]
-
Geuvers H.
Logics and Type Systems.
Ph.D. dissertation, Catholic University Nijmegen, 1993.
- [Gil60]
-
Gilmore P. C.
A proof method for quantification theory: Its justification and
realization.
In IBM Journal of research and development, volume 4, pages
28--35, 1960.
- [Gim94]
-
Giménez E.
Codifying guarded definitions with recursive schemes.
In Types'94: Types for Proofs and Programs, volume 996 of LNCS. Springer-Verlag, 1994.
Extended version in LIP research report 95-07, ENS Lyon.
- [Gim98]
-
Giménez E.
A Tutorial on Recursive Types in Coq.
Technical Report RT-0221, Inria (Institut National de Recherche en
Informatique et en Automatique), France, 1998.
- [GLT89]
-
Girard J. Y., Lafont Y., and Taylor P.
Proofs and Types.
Cambridge Tracts in Theoretical Computer Science. Cambridge
University Press, 1989.
- [Har94]
-
Harrison J.
The QED Manifesto.
In Automated Deduction - CADE 12, volume 814 of Lecture
Notes in Artificial Intelligence, pages 238--251. Springer-Verlag, 1994.
- [Har96]
-
Harrison J.
A Mizar Mode for HOL.
In Joakim von Wright, Jim Grundy, and John Harrison, editors, Theorem Proving in Higher Order Logics: 9th International Conference,
TPHOLs'96, volume 1125 of Lecture Notes in Computer Science, pages
203--220, Turku, Finland, 1996. Springer-Verlag.
- [HKP98]
-
Huet G., Kahn G., and Paulin-Mohring C.
The Coq Proof Assistant. A Tutorial, 1998.
- [Hor99]
-
Horacek H.
Presenting Proofs in a Human Oriented Way.
In 16th International Conference on Automated Deduction, 1999.
- [ISO8879]
-
Standard Generalized Markup Language (SGML).
ISO 8879:1986.
- [Jut94]
-
Jutting van L. S. B.
Checking Landau's ``Grundlagen'' in the AUTOMATH System.
Ph d. thesis, Eindhoven University of Technology, 1994.
Useful summary in Nederpelt, Geuvers and de Vrijier, 1994, 701-732.
- [Luo90]
-
Luo Z.
An Extended Calculus of Constructions.
PhD thesis, 1990.
- [Mac95]
-
MacKenzie D.
The automation of proof: A historical and sociological exploration.
In IEEE: Annals of the History of Computing, 1995.
- [Mas64]
-
Maslow S. J.
An inverse method for establishing deducibility in classical
predicate calculus.
In Doklady Akademii Nauk, volume 159, pages 17--20, 1964.
- [NL98]
-
Necula G. C. and Lee P.
Efficient Representation and Validation of Proofs.
In Proceedings of the 13th Annual symposium on Logic in Computer
Science,, Indianapolis, 1998.
- [NS56]
-
Newell A. and Simon H. A.
The logic theory machine.
In IRE Transactions on Information Theory, volume 2, pages
61--79, 1956.
- [Pau89]
-
Paulin-Mohring C.
Extraction de programmes dans le Calcul des Constructions.
Thèse d'université, Paris 7, January 1989.
- [Pra60]
-
Prawitz D.
An improved proof procedure.
In Theoria, volume 26, pages 102--139, 1960.
- [Ric99]
-
Ricci A.
Studio e progettazione di un modello RDF per biblioteche matematiche
elettroniche, 1999.
- [Rob65]
-
Robinson J. A.
A machine-oriented logic based on the resolution principle.
In Journal of the ACM, volume 2, pages 23--41, 1965.
- [SH95]
-
Saibi A. and Huet G.
Constructive Category Theory.
In Proceedings of the joint CLICS-TYPES Workshop on Categories
and Type Theory, Goteborg (Sweden), January 1995.
- [W3Ca]
-
Extensible Markup Language (XML) 1.0 W3C Reccomendation.
http://www.w3.org/TR/1998/REC-xml-19980210.
- [W3Cb]
-
Mathematical Markup Language (MathML) 1.01 W3C Reccomendation.
http://www.w3.org/TR/REC-MathML.
- [Wan60]
-
Wang H.
Toward mechanical mathematics.
In IBM Journal of research and development, volume 4, pages
2--22, 1960.
- [Wer94]
-
Werner B.
Une Théorie des Constructions Inductives.
Ph.D. dissertation, Universite Paris 7, May 1994.
- [Wer97]
-
Werner B.
Constructive Category Theory.
In Proocedings of the International Symposium on Theoretical
Aspects of Computer Software, 1997.
Ringraziamenti
Un grosso ringraziamento al Prof. Andrea Asperti e ai miei
collaboratori Dott. Luca Padovani e Dott. Irene Schena che hanno
dato vita ad un ambiente di lavoro produttivo e stimolante.
Un ringraziamento sentito al Dott. Benjamin Werner che mi ha introdotto
al sistema Coq e al Dott. Hugo Herberlin che ha pazientemente chiarito i
miei dubbi su CIC.
Ringrazio calorosamente tutti i miei compagni di corso
e tutti i docenti del Dipartimento di Informatica per i
bellissimi e coinvolgenti anni trascorsi all'Università.
In particolare, un grosso ringraziamento va a Valerio Paolini
per i frequenti e costruttivi confronti di idee, sia sul piano
tecnico che su quello umano.
Infine ringrazio la mia ragazza, la mia famiglia e i miei amici
per avermi pazientemente supportato e sopportato durante il mio lungo
periodo di tesi.
This document was translated from LATEX by
HEVEA.